液压支架立柱液压系统阀芯卡滞诊断
2018-09-19,,,,
, ,,,
(山东科技大学 机械电子工程学院,山东 青岛 266590)
作为采煤工作面机械化支护设备,液压支架的动态特性将影响煤矿的生产效率和生产安全[1]。由于液压支架长期处于井下的恶劣环境中工作,并且支架的液压系统较为复杂,支架的故障诊断极其困难[2]。据统计,液压支架故障中有80%以上是由液压系统故障引起的,而液压阀作为支架液压系统的关键元件,其可靠性严重影响支架工作稳定性,研究液压阀的工作性能对提高支架整体可靠性具有重要意义[3]。
立柱在液压支架中承担着调节高度与承载重量的重要角色,当支架在煤矿井下使用时,顶梁将围岩的巨大压力传递给立柱[4],使得立柱长期处于高压状态,故其性能参数决定支架的正常工作。李首滨[5]对国产液压支架电液控制系统技术现状进行了深度剖析,强调了电液控制系统将成为液压支架控制方式的发展潮流;于忠诚等[8]对电液比例阀用控制器的研究,解析电磁阀内部特征及其控制方式的独特性;朱成实等[7]利用AMESim仿真软件研究电液换向阀动态特性,提供了一种利用软件研究电液换向阀的新思路;王如等[8]利用AMESim仿真软件,通过设置不同参数对立柱控制回路的油缸内泄露大、液压锁内泄和安全阀卡滞仿真,得到了支架故障前后的油缸位移和压力曲线,通过曲线对比判断液压系统故障原因,经验证仿真结果准确可靠,为研究液压支架立柱液压系统阀芯卡滞问题提供了一种研究方法。
传统液压系统故障检测方法主要是经验检测法,即维修人员凭借自己多年的生产实践能力诊断出故障所在位置,此方法对维修人员有较高的实践能力要求,这使得传统检验方法存在一定的缺陷。本研究在已有换向阀研究的基础上,搭建适用于本支架的电液换向阀仿真模型,并通过改变电磁先导阀和液控换向主阀阀芯位置上下限,得到不同液压阀故障前后立柱位移、速度、无杆腔流量、无杆腔压力曲线,通过对比分析锁定故障液压阀。与传统检测方式相比,仿真模拟实验结果可靠度高,对维修人员的实践经验没有那么严苛的要求,同时可大大缩短故障检测时间,防止危害事故继续蔓延,提高煤矿生产安全。
1 立柱回路仿真模型的建立及液压系统参数求解
本研究以ZF5600/16.5/26液压支架为研究对象[9],对其立柱液压控制回路进行仿真研究。支架升柱过程中,起主要影响作用的液压阀为电磁先导阀和液控换向阀[10],以不同阀芯开启度大小对支架升柱过程中的影响来反映阀芯卡滞问题。首先通过AMESim仿真软件对立柱液压系统进行建模,考虑到液压系统中电磁先导阀和液控换向阀的开启程度对立柱的影响,因此在仿真建模时采用液压元件设计液压阀模型,以更加精确的研究阀芯开启度对立柱动作的影响,建立立柱控制回路如图1所示[11]。
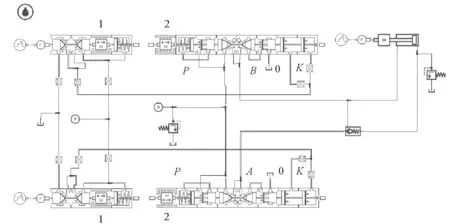
图1 立柱控制回路仿真模型Fig.1 Simulation model of column control loop
在忽略管路沿程阻力损失和通流截面积变化造成压力损失的影响下,计算单个立柱的初撑力Fc和工作阻力Fa为:

(1)
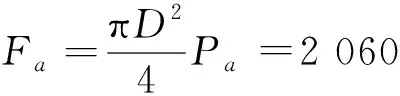
(2)
实际生产中为保证安全,一般情况下立柱实际的承载压力要小于设计的压力,故仿真中设定立柱初撑力为1 300 kN,工作阻力为2 000 kN。
根据图1立柱控制回路仿真模型可知,电磁先导阀的作用是控制液控换向阀阀芯位置[12],故其液阻力只影响液控换向阀的开启度,建立立柱控制回路中的状态方程为:

(3)

(4)
(5)

立柱控制回路中,因不同液压阀之间、液压阀与立柱之间的管路较短,忽略管中液流的惯性[13],故将液阻与液压阀口液阻合并,将液容与立柱两腔的液容合并。

图2 电液换向阀1—主阀芯;2—主阀体;3、7—弹簧;4、5—阀堵;6—电磁铁;8—电磁阀阀座;9—电磁阀阀芯Fig.2 Electro-hydraulic directional control valve
双立柱控制回路是对称单立柱控制回路的组合。在支架升降过程中由于顶梁的作用,不仅能使同一换向阀控制下的立柱基本同步,而且可以使不同换向阀(必须同时开闭)控制下的立柱基本同步[14]。故立柱的升降动态过程可按单柱动态过程分析,只是将泵站输送出来的流量按立柱数目平均,同样流向支路回液管路的流量应是单柱回液流量与立柱数目的乘积。
由式(3)~(5)可知,液控换向阀的液阻将对升柱过程产生阻碍作用,其阻碍作用主要体现在支架运动过程中压力和流量的变化[15],在液压阀选型确定的基础上,换向阀的液阻将主要受阀芯开启度的影响。
电液换向阀的工作原理是电磁先导阀在电磁信号的作用下,克服先导阀左侧复位弹簧的弹力和摩擦力而推动阀杆向左移动,使得换向主阀进液口与阀杆腔相连,同时活塞关闭回液腔节流口,使得P口与A口导通。从液流方向上看,共有4个口,分别是P、T、A、O,其中O口为与先导阀相连接的控制口,电磁先导阀未通电前,O口控制的液流无法进入换向主阀,P口在阀杆右移前为封闭状态,此时A口与T口导通;电磁先导阀通电后先导阀阀杆左移,O口控制的液流推动主阀杆右移,此时T口处于封闭状态,A口通过阀杆、锥头活塞与周向节流口阀体导向P口导通。
对于图2电液换向阀来说,常态时A、T口相通,在外力的驱动下P、A口相通,当滑阀阀芯开口量x变化时,通过滑阀的流量将跟随变化,从而使阀腔内的液流动量发生变化[16]。动量的变化会对阀芯产生一个反作用力,即瞬态液动力Fk,其大小为:

Fk=ρρ (6)

表2 液控换向阀仿真参数Tab. 2 Simulation parameters of hydraulic control reversing valve
忽略阀腔内高压油液的泄漏量和压缩量,则阀内流量处处相等,由节流公式可知流量满足:
(7)
将式(7)代入式(6)可得:
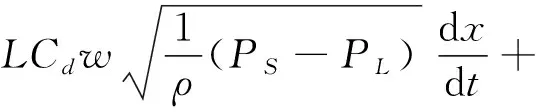
(8)
其中:ρ为液压油的密度,L为阀腔内液压长度,Cd为流量系数,w为面积梯度,PS为供液压力,PL为负载压力,t为时间。由公式(6)可知,瞬态液动力与液压油的加速度方向相反,故可根据液压油加速度方向来判断瞬态液动力方向。
根据懦可夫斯基水击理论,取换向阀内ΔS厚的液体为研究对象,在ΔP作用下,液体密度由ρ变为ρ+Δρ,则此时瞬态液动力为

(9)
由式(9)可知,由于油液的压缩性很小,则Δρ→0,使得Fs→∞,显然压力变化对瞬态液动力影响很大,这也是公式(8)不能忽略的原因。
2 阀芯开启度对立柱液压系统影响的仿真分析
以液压支架立柱液压系统为研究对象,分析立柱在升架、初撑、增阻过程中的动态特性[17]。根据式(1)和式(2),负载分以下五个阶段:①空载上升过程,负载1×105N,时间0~1.5 s;②支撑承载阶段,负载1×105~1.3×106N,时间1.5~2.0 s;③初撑稳定阶段,负载恒定为1.3×106N,时间2.0~2.5 s;④增阻过程,负载1.3×106~2.0×106N,时间2.5~3.0 s;⑤恒阻稳定阶段,负载恒定为2.0×106N,时间3.0~3.5 s[18]。电磁先导阀组成元件的参数设置如表1所示,液控换向阀组成元件的参数设置如表2所示。
ZF5 600/16.5/26液压支架属于单伸缩,立柱缸径为230 mm,杆径为210 mm,行程为0.15 m,活塞杆质量为500 kg;设定恒压源提供压力31.5 MPa,恒流源流量为180 L/min,立柱安全阀设定压力为50 MPa,泵站到支架的主进液管通径为50 mm,主回液通径为65 mm,泵站到支架的主进、回液管长度为200 m。设定仿真起始时间为0 s,结束时间为3.5 s,仿真步长为0.001 s,仿真允许误差10-5,采用标准解算器混合误差进行仿真[18]。
由流体力学中压力损失可知,阀芯位移上下限的改变将增大局部压力损失,其压力损失方式可视为断面突然缩小引起的压力变化,损失值hj满足

(10)
其中:ξ为局部损失系数,A1为最小开口面积,A2为液压阀设计开口面积,v1为油液通过最小开口面积的速度。阀芯卡滞使得油液通过的面积减小,由式(10)可知,不考虑液压油泄露、压缩的前提下,通过液压阀的流速将增大,同时局部损失系数也会增大,故使得局部压力损失增大。
对于控制进液的电磁先导阀,其正常工作时阀芯位移上下限为0.001 m~0,本次设定卡滞时阀芯位移上下限分别为0.000 5 m~0和0.000 1 m~0,由于阀芯位置的变化受外部电磁的控制[19],设定电磁信号变化如图3所示,可得到电磁换向阀阀芯位移如图4所示。

图3 外部电磁控制信号Fig.3 External electromagnetic control signal

图4 进液电磁先导阀阀芯位移曲线Fig.4 Displacement curve of valve core for electromagnetic pilot valve

图5 液控换向阀阀芯位移曲线Fig.5 Displacement curve of spool valve of hydraulic control valve
根据电磁先导阀阀芯位移的不同,仿真得到液控换向阀阀芯位移如图5所示。
由图5可知,电磁先导阀阀芯位移上下限分别为0.000 5 m~0和0.000 1 m~0时,液控换向阀阀芯位移重合,而阀芯位移上下限为0.000 1 m~0时,液控换向阀阀芯位移时间有明显的延迟,时间约为0.2 s,这表明阀芯开启度在0.000 5 m时产生的液阻并不足以影响电磁先导阀对液控换向阀的控制,即进液压力大于液阻与液控换向阀中弹簧压力之和,而在阀芯开启度为0.000 1 m时则产生了较明显的影响,该影响主要体现在时间的延迟上。
液压支架的动态特性图如图6~8所示。
电磁先导阀阀芯开启度的变化反映到支架升柱过程中,主要对位移和速度有较明显影响,而对立柱无杆腔内的压力和流量几乎没有明显波动。由图6可得,阀芯开启度在0.000 5和0.000 1 m时位移重合,最大位置略低于阀芯开启度在0.001 m的时候,图8说明速度在2.0 s以后波动明显,也就是立柱初撑阶段完成,开始进入初撑稳定阶段的时候,此时电磁先导阀阀芯即将复位结束,阀口开启度不断减小直至为零。
对于控制进液的电液换向阀,其正常工作时阀芯位移上下限为0~-0.006 m,本次设定卡滞时阀芯位移上下限分别为0~-0.004 m和0~-0.002 m,如图10所示;电磁换向阀的阀芯位移上下限设为正常值0.001 m~0,其他外部条件均不变[20]。

图6 立柱位移曲线Fig.6 Column displacement curve

图7 无杆腔压力曲线Fig.7 Rodless cavity pressure curve

图8 立柱速度曲线Fig.8 Column velocity curve

图9 无杆腔流量曲线Fig.9 Rodless cavity flow curve
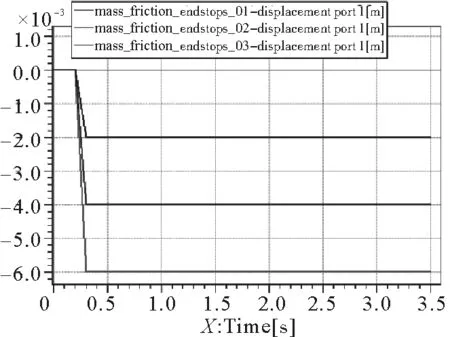
图10 电液换向阀阀芯位移曲线Fig.10 Displacement curve of spool valve of electro-hydraulic reversing valve
在图10电液换向阀阀芯开启度不同的情况下,仿真得到立柱升柱时的动态特性曲线如图11~14所示。
由图11和图14可知,液控换向阀阀芯开启度的减小使得位移和流量出现类似成比例的减小;当阀芯开启度在0.002 m时,结合图12可知,立柱活塞杆只在原位置出现上下振动,活塞杆并没有伸出去支撑顶板,即出现支架压死现象;当阀芯开启度为0.004 m时,支架在没有达到支撑高度时便进入了初撑阶段,即顶板来压时间提前于支架完成升架的时间,将导致顶板下沉严重,出现冒顶事故。
由图12~13可知,阀芯开启度越小,将使得速度和压力波动越明显。支架在升柱阶段,即仿真前2 s时,阀芯开启度对无杆腔压力影响较小,速度波动略有变化,而在2.0 s以后,即立柱进入初撑阶段以后,由于外力的存在,尤其开启度为0.002 m时,速度和压力曲线均波动非常剧烈,立柱活塞杆将随之震荡剧烈,影响支架整体稳定性。
3 结论
通过分析不同液压阀阀芯开启度对立柱液压系统的影响,得到以下结论:
1) 由立柱控制回路状态方程可知,影响立柱压力、流量的变化因素有液控换向阀液阻、液控单向阀液阻、立柱阀芯质量、立柱两腔的液容以及顶板作用力。
2) 电磁先导阀阀芯开度对立柱液压系统的影响是间接通过控制液控换向阀的开启来实现的。当电磁先导阀阀芯开启度过小,使得液控先导阀阀芯开启时间晚于正常工作状况,此时对立柱的影响主要反映在速度的变化上。
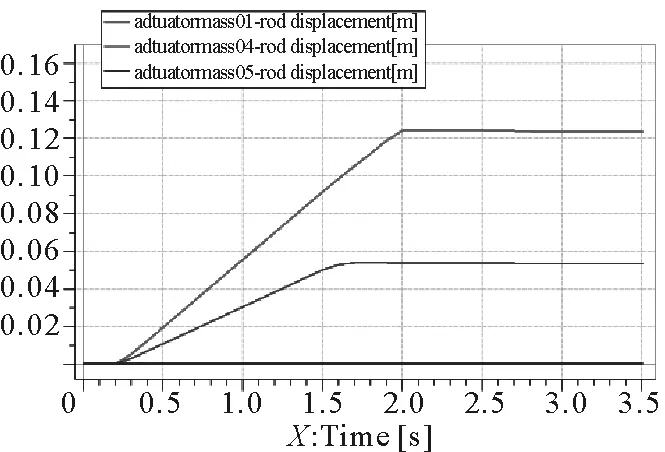
图11 立柱位移曲线Fig.11 Column displacement curve
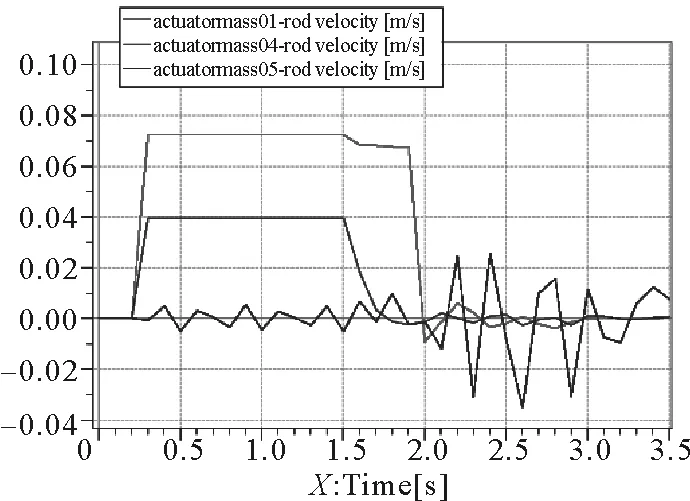
图12 立柱速度曲线Fig.12 Column velocity curve

图13 无杆腔压力曲线Fig.13 Rodless cavity pressure curve

图14 无杆腔流量曲线Fig.14 Rodless cavity flow curve
3) 液控换向阀阀芯开启度对立柱液压系统的影响是直接性的,由于阀芯开启减小,使得液阻变大,导致支架仿真曲线都变化剧烈。当阀芯开启度为0.002 m时,在实际工况下,将会出现顶板垮落事故,危害极大,必须极力避免此类危害的发生。
通过AMESim仿真软件建立ZF5600/16.5/26液压支架立柱液压系统,通过对立柱控制回路的电磁先导阀、液控换向阀阀芯卡滞故障进行仿真研究,得到立柱故障前后的位移、速度、压力、流量曲线,通过曲线对比可快速锁定立柱液压系统故障阀,为准确有效排除故障提供依据。
