有外部扰动的随机纯反馈非线性系统的自适应模糊控制

,

(山东科技大学 数学与系统科学学院, 山东 青岛 266590)

近年来, 非线性系统的控制问题广泛存在于物理设备的研究中, 如生物光学、机械执行器等, 因此对于非线性系统的控制方案已有很多研究成果[1-4]。 特别的, 一些以线性逼近为基础的自适应控制方案已经从确定非线性系统[5-7]扩展到随机非线性系统[8-11]。 文献[8]研究了具有未知时间延迟的单输入单输出严格反馈非线性随机系统, 提出了一种自适应模糊控制方案。文献[9]针对一类不确定随机非线性严格反馈系统提出了两种自适应模糊输出反馈控制方法。 文献[10]设计了一个模糊状态观测器来估计未测量的状态, 研究一类具有不可估量状态的不确定随机纯反馈非线性系统的自适应模糊输出反馈问题。 此外, 通过结合模糊逻辑系统的逼近能力和反推技术,非线性系统已经成为研究模糊控制问题的重要工具。 文献[11]考察了非严格反馈形式的单输入单输出非线性随机系统的自适应模糊控制问题, 其中用模糊逻辑系统来逼近不确定非线性函数, 并采用反推技术构建了自适应模糊控制器。 文献[12]针对一类具有非严格反馈形式和未知非线性死区的非线性系统的自适应模糊跟踪控制问题, 基于模糊逻辑系统的逼近能力和反推技术, 提出了自适应模糊控制方案。 然而, 上述结果中的未知函数都是仿射形式的, 即输出的状态方程是线性形式。

纯反馈非线性系统中的未知函数是无仿射形式。 对于纯反馈非线性系统, 基于中值定理,先后提出了一些自适应模糊控制方案[13-15]。 文献[13]针对一类具有时变延迟的不确定随机纯反馈系统, 提出了自适应神经控制方案。 文献[14]提出了一类具有未知滞后的随机纯反馈非线性系统的自适应模糊控制方案。 文献[15]对于随机纯反馈非线性系统, 提出了一类自适应神经网络控制方案。 然而, 这些研究忽略了外部扰动的影响。 在实践中, 外部扰动时常是系统不稳定的来源, 带有外部扰动的系统对于自适应率和虚拟控制信号的设计有着更高的要求, 带有外部扰动的系统比一般系统的研究更加困难。 近年来, 对于带有外部扰动的系统研究有了一些结果[16-19]。 而对于带有外部扰动的随机纯反馈非线性系统的研究成果较少。

不同于文献[20]研究的是确定系统, 也不同于文献[21]中忽略了外部扰动，本文研究的是有外部扰动的随机纯反馈非线性系统的自适应模糊控制问题。 利用中值定理, 结合反推方法, 提出了一种新的自适应模糊控制方案。

1 准备工作和问题陈述

先介绍以下随机非线性系统:

dx=f(x,t)dt+h(x,t)dw,

(1)

其中,x∈Rn是状态变量,f:Rn×R+→Rn,h:Rn×R+→Rn×r是连续函数。w是定义在完备概率空间(Ω,F,{Ft}t≥0,P)上的r维独立标准布朗运动, 其中Ω是样本空间,F表示σ域, {Ft}t≥0表示范围,P是概率测度。

定义1[22]对于二次连续可微函数V(x,t), 定义一个微分运算符L, 则:

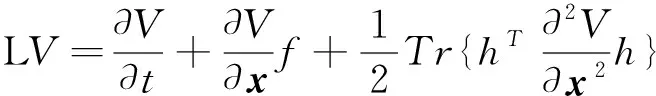
(2)

其中,Tr是矩阵的迹。

考虑以下带有外部扰动的随机非线性系统:

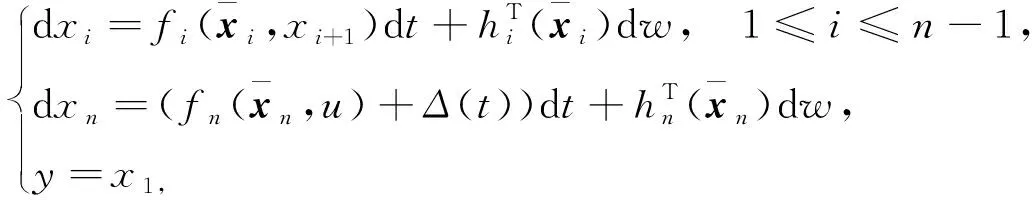
(3)

对于系统(3), 定义:

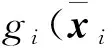
(4)

其中xn+1=u。

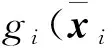
(5)

使用模糊逻辑控制系统来逼近定义在完备集Ω上的一个连续函数f(x)。 采用单点模糊化和中心平均模糊化推论得到以下模糊规则[14]:

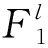
thenyisGl,l=1,2,…,N。

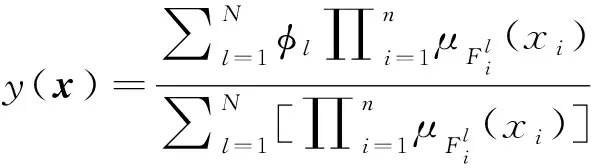
(6)

其中

令

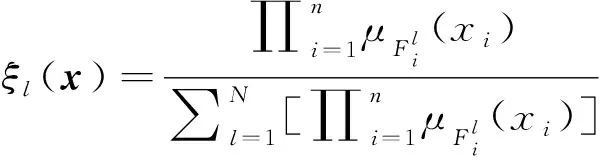
模糊逻辑系统(6)可以重新写为

y(x)=φTξ(x)。

(7)

引理1[14]设f(x)是定义在完备集Ω上的连续函数。 对∀ε>0, 存在一个模糊逻辑系统(7), 使得

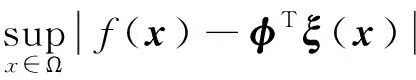
(8)

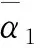
则存在系统(1)的一个特解, 对每一个x0∈Rn, 满足:

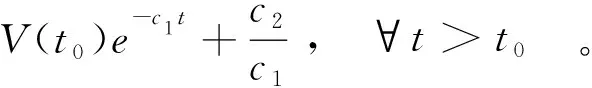
(9)

并且V(x,t)是有界的。

引理3[24]对∀(x,y)∈R2, 以下不等式成立:

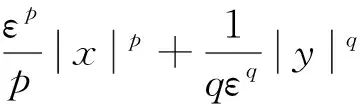
其中ε>0,p>1,q>1,(p-1)(q-1)=1。

引理4[24]考虑以下动态形式:

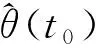
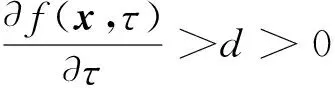
f(x,τ*)=0。

(10)

控制目标是: 设计一个自适应模糊控制方案, 使得系统输出y跟踪到参考信号yd, 并且闭环系统的所有信号是有界的。

假设2参考信号yd(t)以及它的n阶导数, 都是连续有界的。

2 设计自适应控制器

现在利用反推方法, 设计非线性系统(3)的自适应控制方案。 定义以下坐标变换:

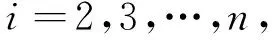
(11)

其中αi-1是一个中间控制函数。

第1步考虑系统(3), 由z1=y-yd, 知动态误差满足

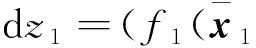
(12)

选择以下Lyapunov函数

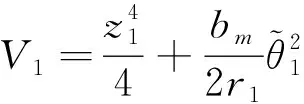
(13)

其中r1是正常数。 由式(2)和式(11)、(12), 知

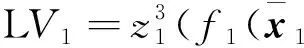
(14)

根据引理3, 以下不等式成立

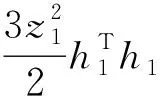
(15)

其中l1是正常数。 将(15)代入(14)式, 有

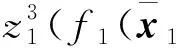
(16)

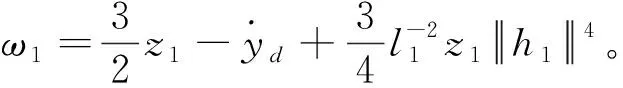
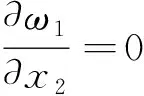
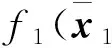
(17)

根据中值定理, 存在μ1(0<μ1<1), 使得

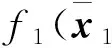
(18)

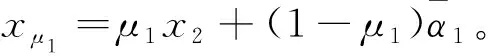
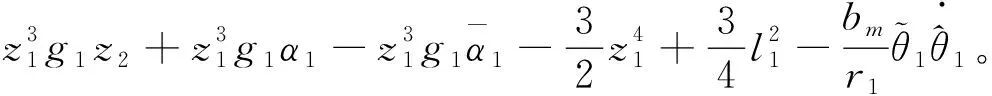
(19)

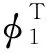
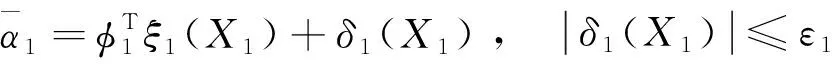
(20)

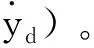
(21)

其中a1是正常数。 选择虚拟控制信号和自适应率分别为

(22)

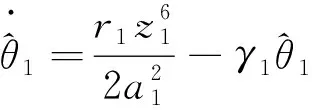
(23)

其中k1和γ1是正常数。 由(25)和假设1知

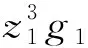
(24)

再由引理2及假设1, 得

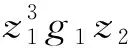
(25)

把式(21)～(25)代入式(19), 得

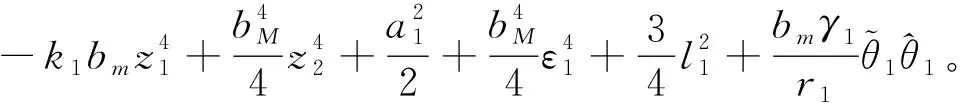
(26)

又

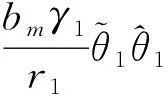
(27)

所以式(26)可以化为

(28)

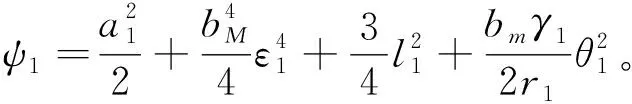
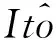
(29)

其中

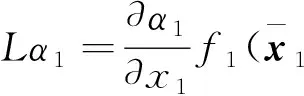
(30)

选择以下Lyapunov函数

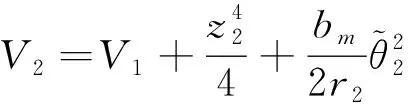
(31)

其中r2是正常数。 由式(2)和式(29), 有

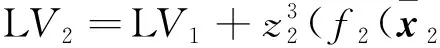
(32)

由引理3, 得

(33)

其中l2是正常数。 将式(28)、(33)代入式(32), 有

(34)

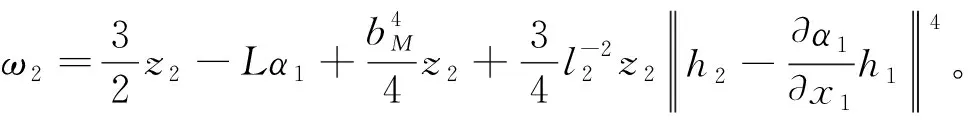
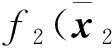
(35)

根据中值定理, 存在μ2(0<μ2<1), 使得

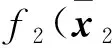
(36)

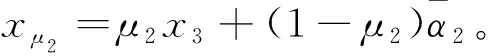
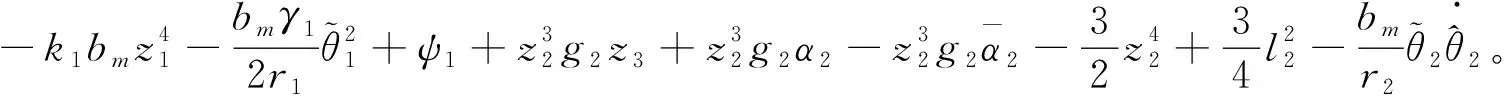
(37)

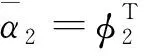
(38)

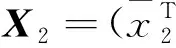
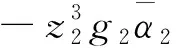
(39)

其中a2是正常数。 选择虚拟控制信号和自适应率分别为

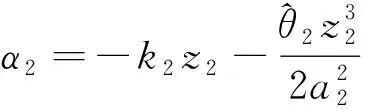
(40)

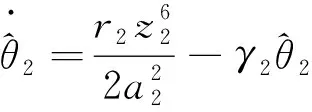
(41)

其中k2和γ2是正常数。 由式(40)和假设1知

(42)

再由引理2及假设1, 得

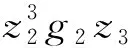
(43)

注意到

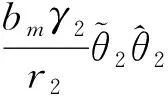
(44)

把式(39)～(44)代入式(37), 得

(45)

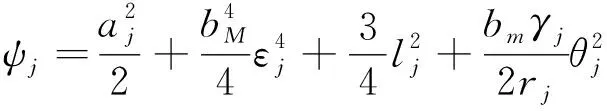
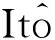
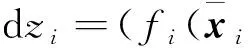
(46)

其中

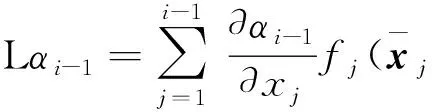
(47)

选择以下Lyapunov函数：

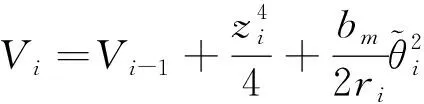
(48)

其中ri是正常数。 由(2)和(46), 有

(49)

由引理3, 得

(50)

其中li是正常数。 将(50)代入(49)式, 有

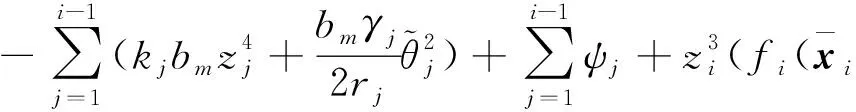
(51)

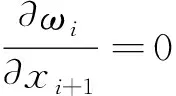
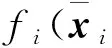
(52)

根据中值定理, 存在μi(0<μi<1), 使得

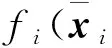
(53)

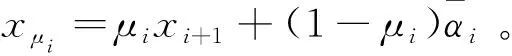
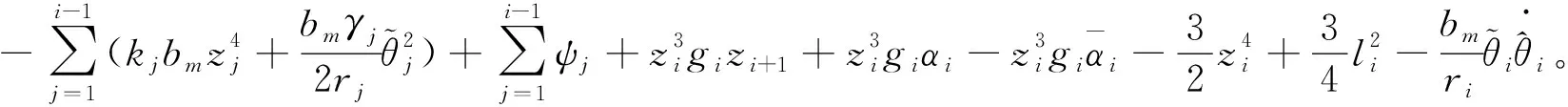
(54)

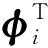
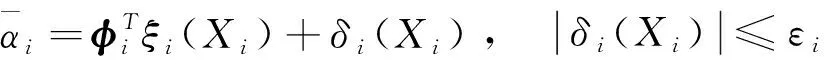
(55)

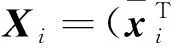
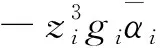
(56)

其中ai是正常数。 选择虚拟控制信号和自适应率分别为

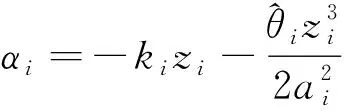
(57)

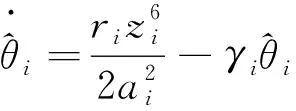
(58)

其中ki和γi是正常数。 由(57)和假设1知

(59)

再由引理2及假设1, 得

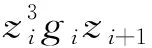
(60)

注意到

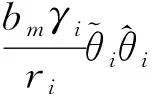
(61)

把式(56)～(61)代入式(54), 得

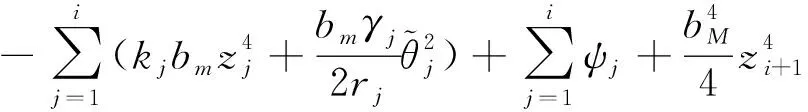
(62)

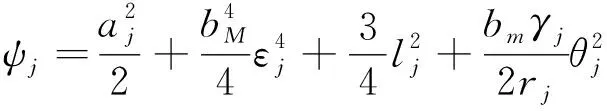
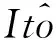
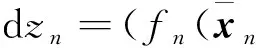
(63)

其中Lαn-1是(47)式取i=n。 选择以下Lyapunov函数

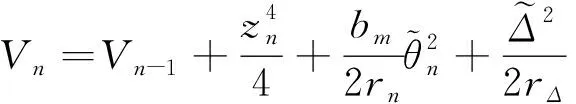
(64)

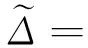
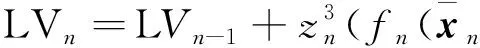
(65)

由引理3, 得

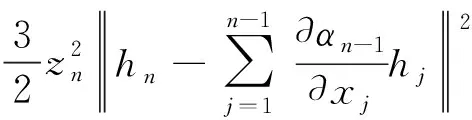
(66)

其中ln是正常数。 将(66)代入(65)式, 有

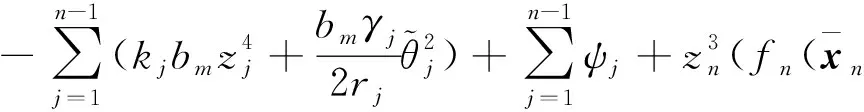
(67)

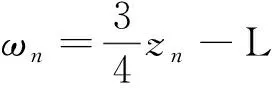
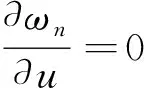
(68)

根据中值定理, 存在μn(0<μn<1), 使得

(69)

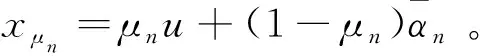
(70)

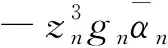
(71)

其中an是正常数。 选择虚拟控制信号和自适应率分别为

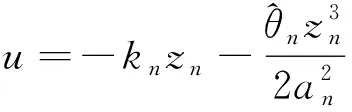
(72)

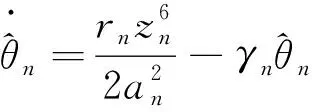
(73)

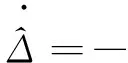
(74)

其中kn、γn和σΔ是正常数。 把式(71)～(74)代入式(70), 得

(75)

又

式(75)可以重新写为

(76)

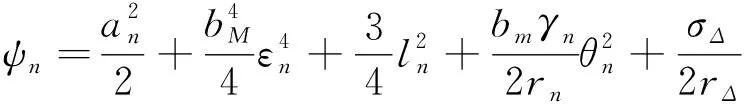
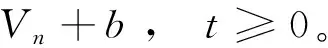
(77)

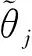
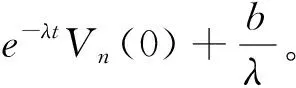
(78)

故

(79)

从而

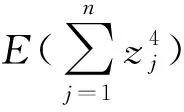
(80)

因此,zj收敛到完备集ΩZ, 其中

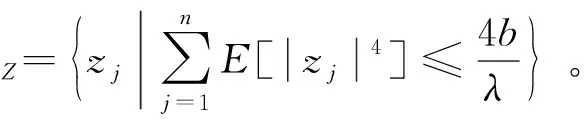
(81)

基于反推技术, 自适应模糊控制器设计完成, 有如下结论。

定理1在假设1和2及初始条件下, 对于随机纯反馈非线性系统(3), 通过设计虚拟控制信号(57)和(72), 以及自适应率(58)和(73)～(74), 保证了闭环系统的所有信号一致有界, 并且跟踪误差收敛到原点的小领域。

3 仿真算例

为了说明所提出方案的有效性, 考虑以下二阶随机纯反馈非线性系统:

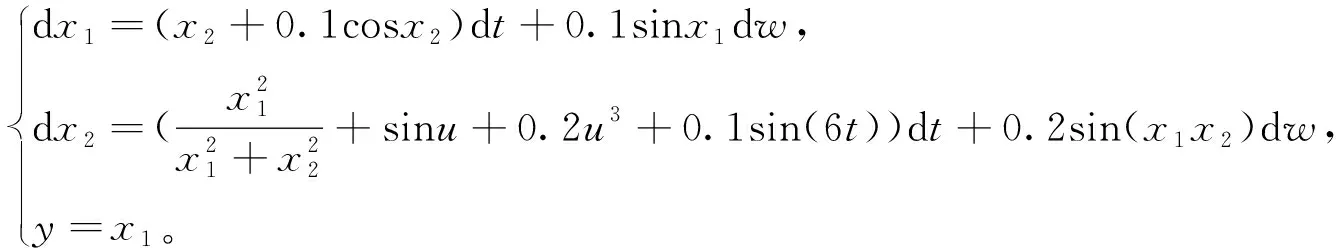
(82)

控制目标是设计一个自适应模糊控制器, 使得闭环系统的所有信号是有界的, 并且系统输出y跟踪到参考信号yd=0.5cost+sin(0.5t)。 根据定理1, 选择以下的虚拟控制信号和自适应率:

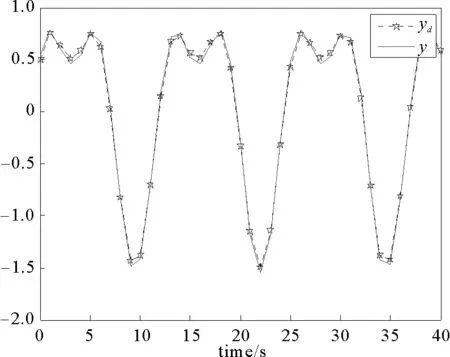
图1 系统输出y和参考信号ydFig.1 System output yand reference signalyd

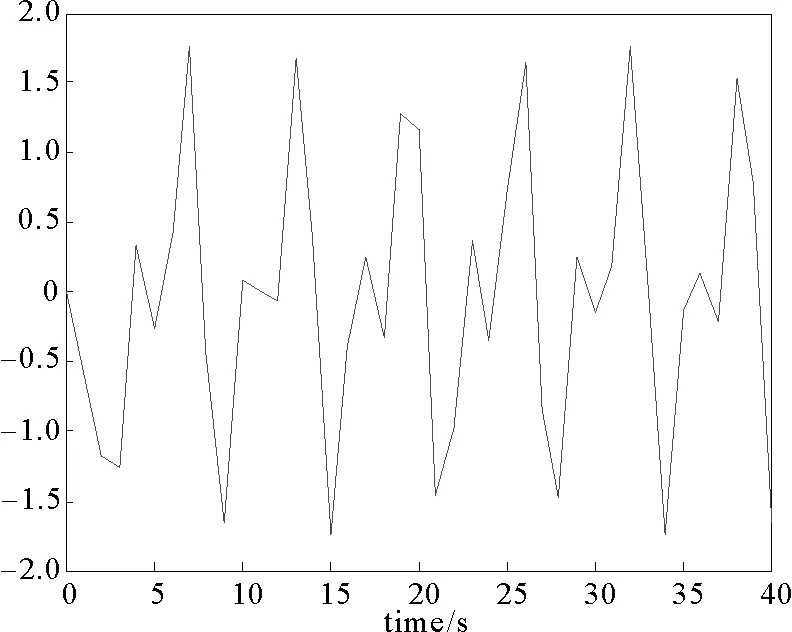
图2 状态变量x2Fig.2 State variable x2

图3 系统输入uFig.3 System output u

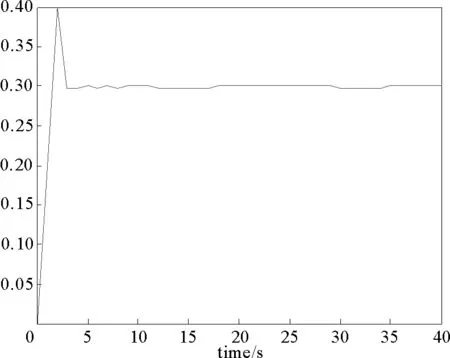
图4 有界外部扰动的估计

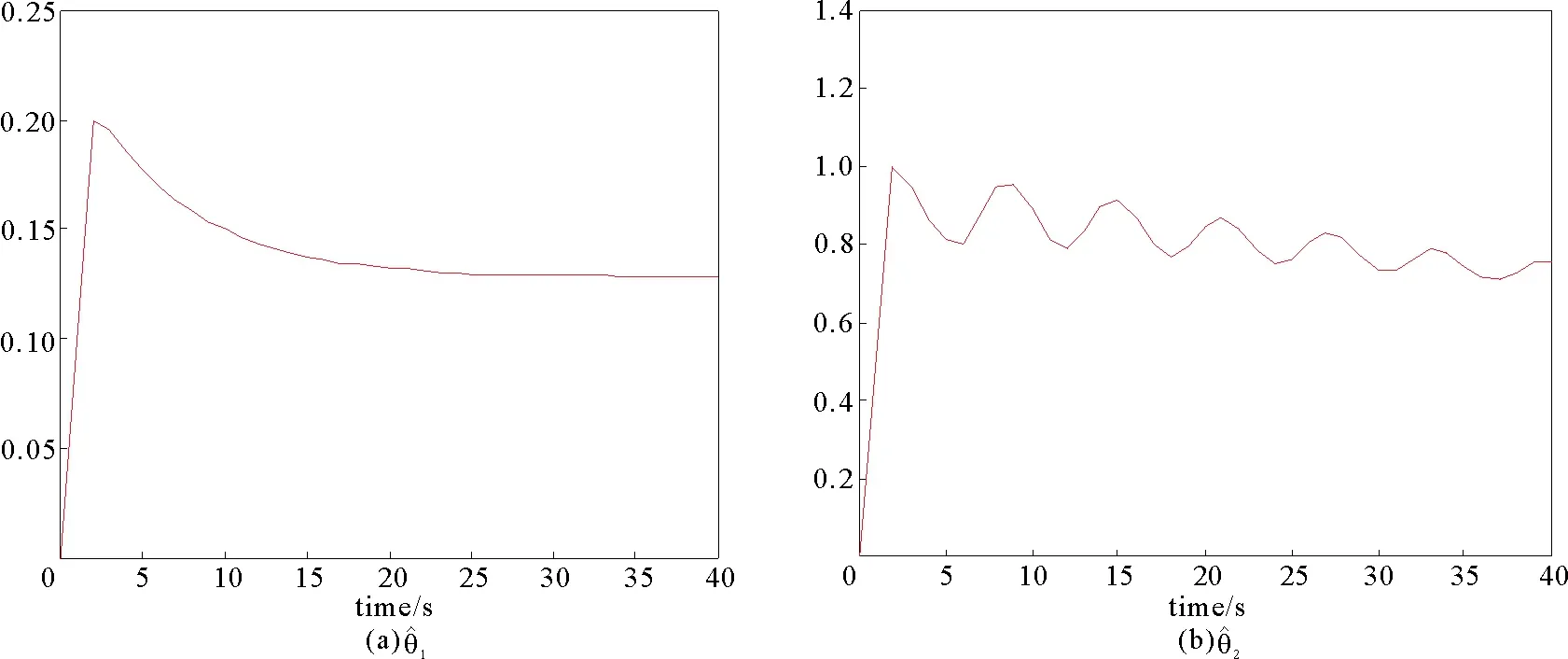
图5 自适应率和Fig.

仿真结果表明了所提出方案的有效性, 保证了系统输出跟踪到参考信号, 并且闭环系统的所有信号是有界的。

4 总结

针对一类具有外部扰动的随机纯反馈非线性系统的跟踪控制问题, 利用中值定理结合反推技术, 设计了一个新的自适应模糊控制方案。 该控制方案保证了闭环系统的所有信号是有界的, 并且跟踪误差收敛到原点的小领域。