城市主干路交叉口直行待行区相位差优化模型
2018-09-19,,,
, , ,
(山东科技大学 计算机科学与工程学院,山东 青岛 266590)
研究数据表明,在日常出行中交通延误占到总出行时间的30%左右,其中交叉口的延误占总延误的50%以上[1],在个别城市,交叉口的延误甚至占到总延误的80%以上[2]。故减少交叉口的延误,对提高道路的通行能力有很重要的意义。尚申德等[3]分析了直行待行区的设置方法和设置长度,并通过北京市区内一典型四相位交叉口证明了直行待行区的合理设置能够减少车辆平均延误,提高进口车道的利用率;左天福等[4]阐述了直行待行区的含义并初步分析了直行待行区设置的原则和适用条件,并对比了虹梅—宜山交叉口直行待行区设置前后的交通效益指标,证明了合理的设置直行待行区能够减少平均延误;李颖宏等[5]深入研究了交叉口是否设置直行待行区通行能力和延误模型的异同,并通过实例交叉口和仿真结果证明了直行待行区的能够降低车均延误;刘梅等[6]建立了以最短排队长度、最大直行进口道通行能力、最小车均停车率为优化目标的交叉口直行待行区时空资源集成多目标优化模型,通过Vissim仿真,证明了合理设置直行待行区能够提高交通运行效益和环境效益;林芬等[7]基于节能减排确定了设置直行待行区的最优条件,通过实例仿真得到了设置直行待行区能够减少车均延误,提高行车效率;杨林等[8]基于排队长度模型确定了直行待行区的临界条件,并通过实例仿真证明了设置直行待行区能够减少车辆延误,提高通行能力。
上述研究都证明了合理设置直行待行区能够减少延误,提高路网的通行能力。但是上述直行待行区的研究均为单路口的情况,整条主干路未达到最佳的通行状态[9]。合理的相位差能够使整条主干路达到最大交通流量和最高的服务水平[10],但上述研究对直行待行区的研究均停留在静态阶段,未考虑相位差的协调,整条主干路的通行状态不是最优的。本研究以设置直行待行区的主干道的最小车辆延误为目标,从上下行两个方向的延误出发,建立了城市主干路交叉口直行待行区相位差优化模型,并采用遗传算法求解延误最小时的最优相位差,针对3个交叉口路况实例,以相位差为0和最优相位差分别在Vissim平台进行仿真,证明了该模型使各交叉口的延误均有不同程度的减小,其中总延误的减小为16.3%。
1 问题描述
假设路网中某主干路有n个交叉口,其中m个交叉口设有直行待行区。一般交叉口的示意图如图1所示,设有直行待行区的交叉口如图2所示。Si表示第i个交叉口,交叉口Si和交叉口Si+1之间的距离为li,直行待行区长度为Li。根据直行待行区设置应该具备的条件,特作以下假设:
1) 交叉口至少要是四相位;
2) 车道设有专门的左转车道;
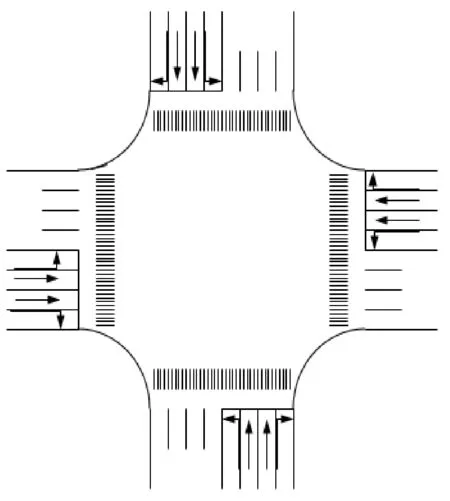
图1 一般交叉口Fig.1 General intersection
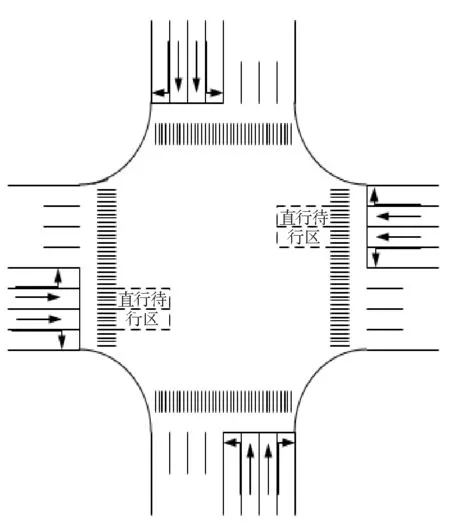
图2 设有直行待行区的交叉口
3) 车辆以均匀的随机到达率和均匀的随机消散率到达和离开交叉口,到达率和消散率互不影响;
4) 交叉口有足够的消散能力,不会出现二次排队的情况;
5) 将黄灯时间看做红灯时间;
6) 交叉口的初始排队长度均为0。
2 模型建立
2.1 交叉口直行待行区相位差优化模型
上下行延误的计算原理一致,故以车辆由交叉口Si+1上行至交叉口Si的延误计算为例进行具体分析。
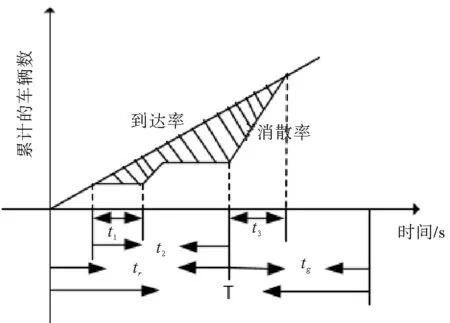
图3 设有直行待行区的交叉口延误
若交叉口Si设有直行待行区,直行待行区长度为Li,车辆到达交叉口Si的第二停车线时遇红灯停车,后续车辆以均匀的随机到达率σ1到达并形成排队。异向绿灯开启后车辆以均匀的随机消散率ζ1驶向直行待行区并在第一停车线处进行等待,之后车辆继续排队至本相位绿灯启亮,此时车辆以均匀随机消散率ζ1开始消散,直至车辆完全消散。其延误如图3所示。
其中,红灯时间为tr,绿灯时间为tg,车辆在第二停车线停车至异向绿灯开启经过的时间为t1,车队头部到达交叉口Si的第二停车线至Si本相位的红灯结束的时间为t2,本相位绿灯启亮至车辆全部消散的时间为t3。图中阴影部分的面积为一个周期T内该交叉口的延误总值。
车辆由Si+1上行至Si的速度为v1,则行驶时间为li/v1,Si相对于Si+1的相位差为φi,i+1,那么有
[li/v1](modT)+t2=φi,i+1,
(1)
由公式(1)可知:
t2=φi,i+1-[li/v1](modT),
(2)
车辆在t2和t3时间段内均以均匀随机到达率σ1到达,当异向绿灯启亮时车辆进入直行待行区,所需时间为Li/v1,当本向绿灯启亮时经过t3时间段以均匀随机消散率ζ1完全消散。根据车辆守恒定律可得
σ1(t2+t3)=ζ1(t3+Li/v1),
(3)
经过化简可得
t3=(σ1t2-ζ1Li/v1)/(ζ1-σ1)。
(4)
则从Si+1上行至Si的延误
将式(2)代入式(5)可以得到Si+1上行至Si的延误
(6)
同理,可得Si-1下行至Si的延误di,d:
(7)
其中v2为车辆下行速度,σ2为下行车辆到达率,ζ2为消散率,φi,i-1为Si相对于Si-1的相位差,t1,为车辆在Si停车至异向绿灯开启的时间。
2.2 主干路交叉口直行待行区相位差优化模型
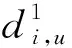
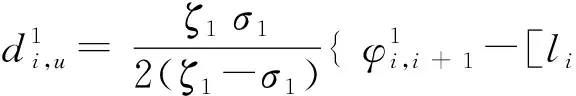
(8)
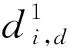
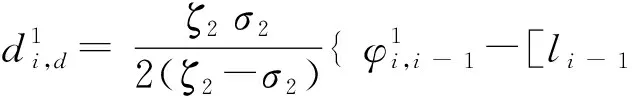
(9)
假设路网中某主干路共有n个交叉口,其中m(m≤n)个交叉口设有直行待行区。对于主干路的起点S1和主干路的终点Sn只考虑离开主干路车辆产生的延误,即对于S1来说只是考虑交叉口S1下行至交叉口S2的延误,对于Sn来说只是考虑交叉口Sn上行至交叉口Sn-1的延误。
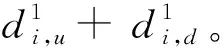
整条主干路的交叉口总延误D为S1下行至S2的延误、Sn上行至Sn-1的延误和其余各交叉口的上下行延误之和,用公式11表示。
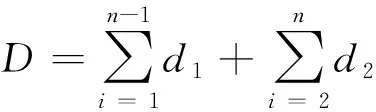
(11)
其中d1和d2分别为上行延误和下行延误并满足公式12。
(12)
综上所示,整条主干路交叉口的总延误
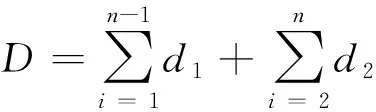
其中约束为:
(13)
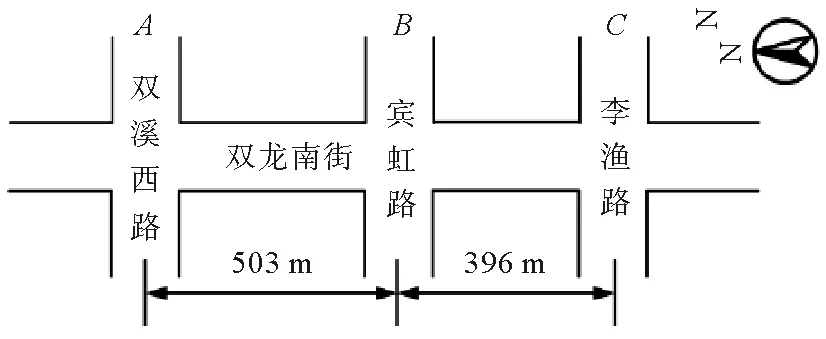
图4 路段长度
3 模型仿真
3.1 交通实例路况
交通实例采用金华市与双龙南街交叉的3个交叉口,为了叙述简便,交叉口从左至右依次记为交叉口A、B、C。金华未设置直行待行区,故假设在宾虹路和双龙南路的交叉口设置了长为12 m的直行待行区,其路段长度和交通流量如图4和图5所示。
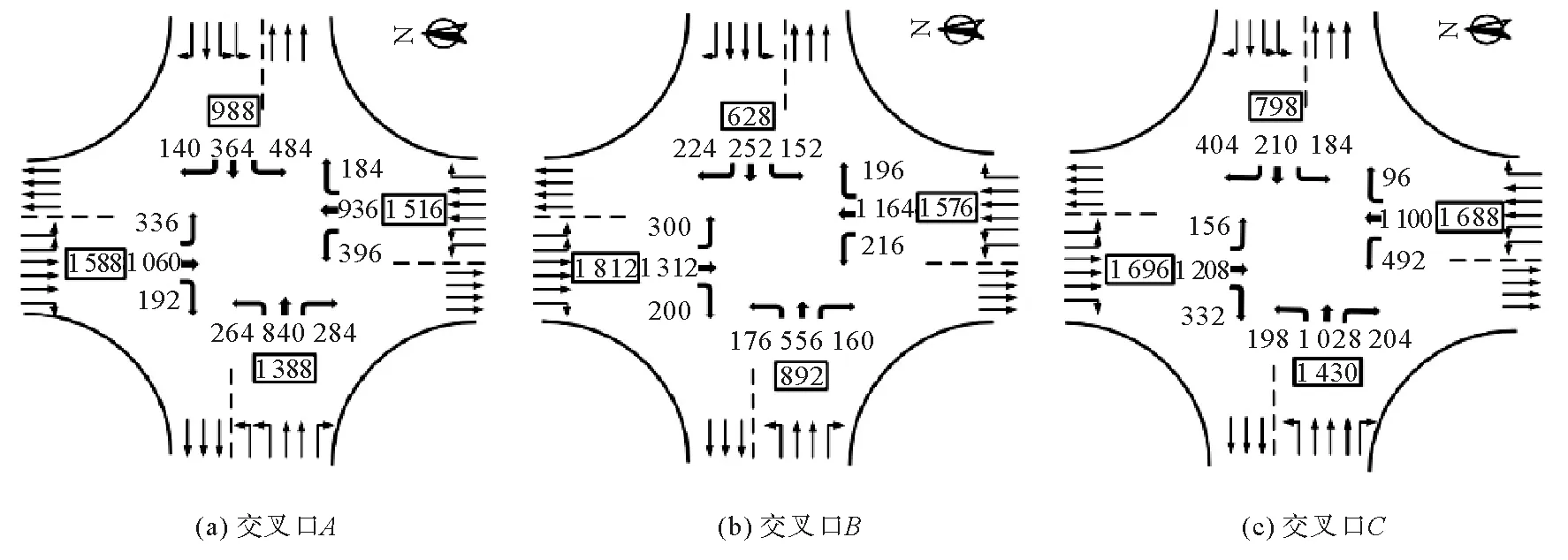
图5 各交叉口流量
3个交叉口均采用4相位,信号周期为124 s,各交叉口的各周期的绿灯时长如表1。

表1 3个交叉口的绿灯时长
图6 交叉口B的Vissim仿真图
3.2 路况仿真
对于相位差的求解采用遗传算法,其中种群个数40,迭代次数为200次,采用二进制编码,变异概率为0.1,交叉概率为0.7,求解得到各交叉口的相位差分别为φBA=36,φCB=64,φBC=60,φAB=88。
采用金华市双龙南的3个交叉口的路况,以原相位差和求得的相位差分别在Vissim平台进行仿真,交叉口B的Vissim仿真如图6所示。
仿真结果采用不同的随机种子数多次仿真求其平均值,其结果如表2。
由表2可知,各交叉口的延误均有不同程度的减小,其中总延误的减小值为18.9%。
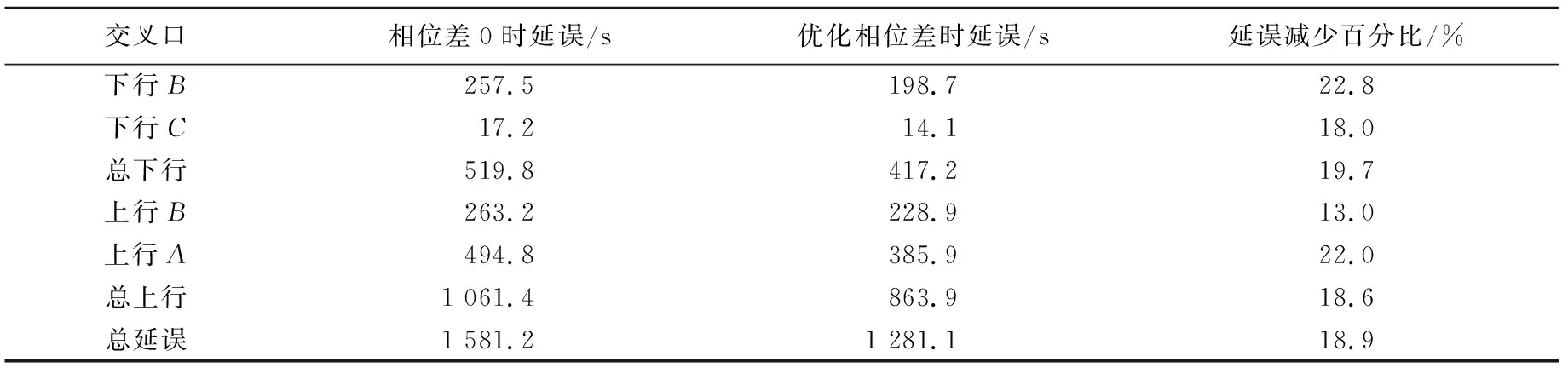
表2 Vissim仿真结果
采用文献[11]的相位差模型计算最优相位差,其结果为φAB=36,φBC=65,φCB=60,φBA=89。文献[11]和本文求得相位差不同在于φBC和φBA的值,此时受影响的交叉口为下行方向的交叉口C和上行方向的交叉口A,其延误如表3。

表3 待行区设置与否的最优相位差下的延误对比
由表3可知,直行待行区存在情况下,本文模型下的延误更小,证明了模型的有效性。
为了进一步说明本文方法的效果,下面与相位差优化模型的几种典型求解算法进行对比分析。求解相位差优化模型常用的解法为:图解法和数解法。图解法是通过几何作图,建立时间-距离图,反复调节速度和周期时长来达到最优的相位差。遗传算法较图解法计算过程更简洁,计算速度更快,结果更直观。下面通过仿真对相位差优化模型中的数解法进行比较。
数解法求解得到的相位差为:φBA=41,φCB=77,φBC=47,φAB=83。通过Vissim仿真得到两个算法延迟的对比如表4。
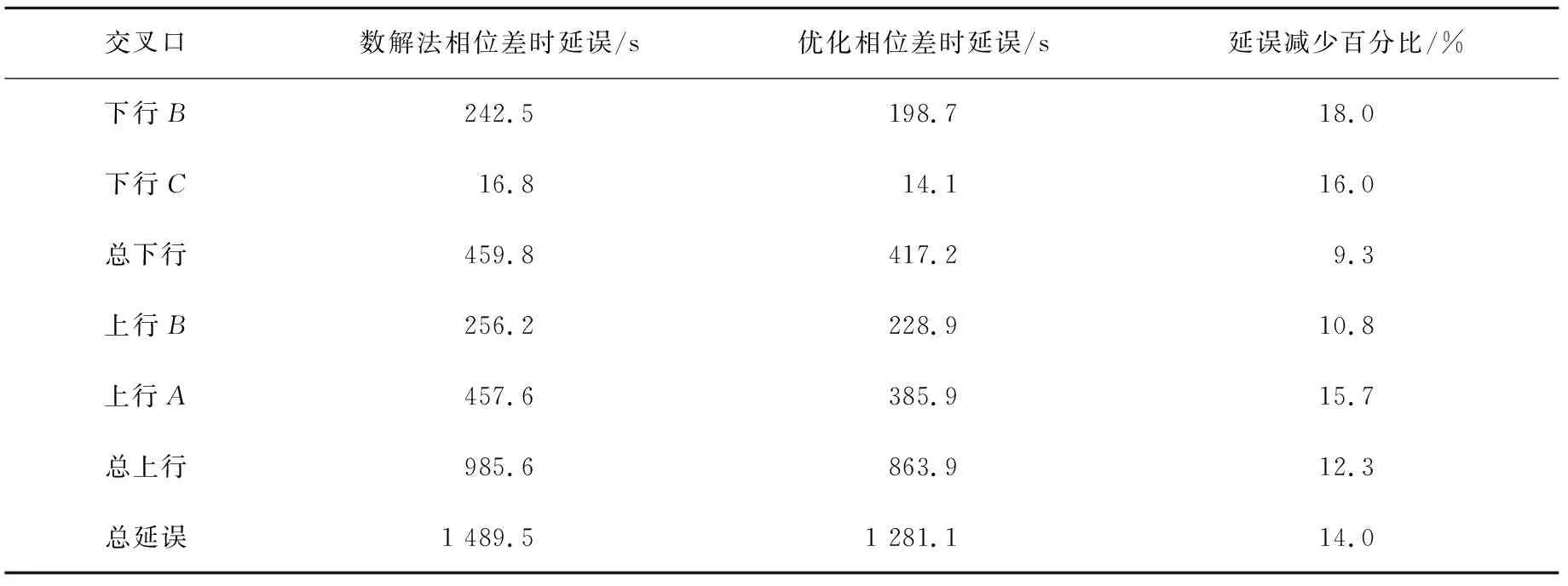
表4 数解法和本文采用遗传算法求解相位差的延误对比
可以看出,本文采用遗传算法求解相位差的求解结果比相位差优化模型中的数解法求解结果更优。
综上,分析得到交叉路口数量、车辆数量、车辆速度对仿真结果的影响:车速增大则延误会减小,车速减小则延误会增大;若消散率不变,则车辆数量增大则会增大延误,车流量数量减小,则会减小延误;在到达率和消散率不变的情况下,交叉口数量的多少对延误无影响。
4 结论
本文分析了交叉口直行待行区的上下行延误,并结合一般交叉口的上下行延误建立了主干路交叉口直行待行区相位差优化模型。采用遗传算法求解最优相位差,在Vissim平台对路况进行仿真,仿真结果证明了模型的有效性。但是本文还存在一定的不足,如车辆速度为定值,且只考虑了队头延误,将在以后的研究工作中进一步改进。
