多种运输方式的4PL多到多网络设计模型与算法

李 锐，孙福明

辽宁工业大学 电子与信息工程学院，辽宁 锦州 121001

1 引言

物流业务外包已经成为许多企业提高自身的核心竞争力的有效途径。随着经济全球化的发展，往往需要多个物流公司合作才能完成一项物流任务。由于能够整合不同的第三方物流（3PL）资源，依靠其信息方面的优势，解决单独靠一家3PL不能完成的任务，第四方物流[1]（4PL）开始得到关注。在运作过程中，4PL需要根据需求设计合理的物流网络来提供有效的物流服务。现实中，很多情况需要承担多个确定的供需点对之间的配送任务，即多到多的配送任务。目前，4PL网络设计问题已经得到一定的研究[2-4]。然而，这些研究都是考虑4PL承担某种产品的配送或回收任务。

此外，3PL运输供应商可能提供多种运输方式供选择，所以在4PL网络设计过程中需要同时考虑选择3PL运输商及运输方式。可见，研究多种运输方式的4PL多到多网络设计问题具有现实意义。目前，国内外学者已经对考虑多种运输方式的物流及运输相关问题进行了研究。Ghorbani[5]研究配送网络的选址库存问题，并考虑多种运输方式和3PL运输供应商。Haddad-Sisakht等[6]研究不确定下考虑多种运输方式的闭环供应链网络设计问题。Masoud等[7]研究多种运输方式对汽车供应链可持续性的影响。郭等[8]对多种运输模式下的生产运输问题进行了研究。然而，考虑多种运输方式的4PL多到多网络设计问题则还没有得到关注。

本文研究考虑多种运输方式的4PL多到多网络设计问题。与现有4PL网络设计问题不同，文中在4PL承担多供需点对物流配送任务情况下同时考虑3PL具有多种运输方式，建立问题的数学优化模型，并设计混合蛙跳算法求解。最后，通过仿真实验来验证模型的合理性及算法的有效性。

2 问题描述及模型

考虑4PL负责多个供需点对之间产品的物流配送任务，并通过3PL服务节点和3PL运输供应商来完成，其中每个3PL运输供应商提供多种运输方式。多到多配送下的4PL网络可表示为无向多重图，如图1所示。网络的节点包括供应点、需求点和3PL服务节点（配送中心、仓库等），网络的边表示3PL运输供应商。多种运输方式的4PL多到多网络设计问题是通过选择3PL服务节点、3PL运输供应商及运输方式来确定网络结构，在各个供需点对的配送时间满足要求的条件下，最小化网络总成本。

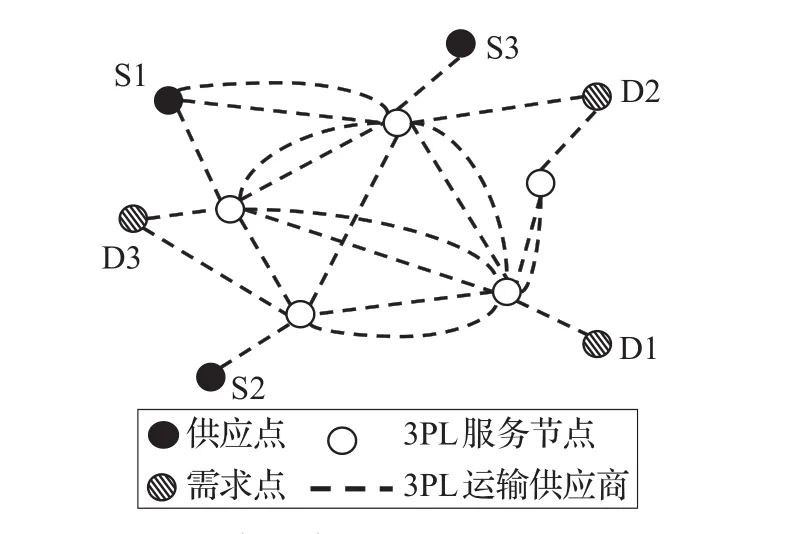
图1 多到多配送下的4PL网络

2.1 符号说明

问题模型的相关集合、参数及决策变量分别如表1和表2所示。

2.2 优化模型

基于以上符号说明和变量定义，建立多种运输方式的4PL多到多网络设计优化模型如下：

（1）目标函数

表1 集合及参数

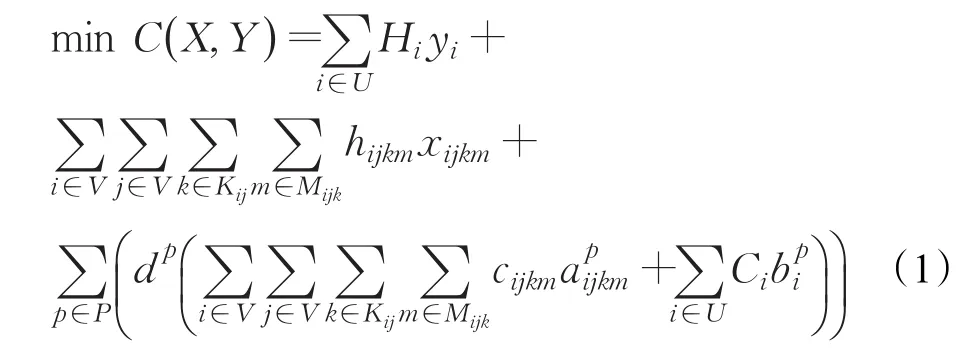
目标函数式（1）最小化总的物流成本，包括3PL服务节点、3PL运输供应商某种运输方式的开设成本，所有供需对点之间产品的运输和处理成本。

（2）配送时间约束

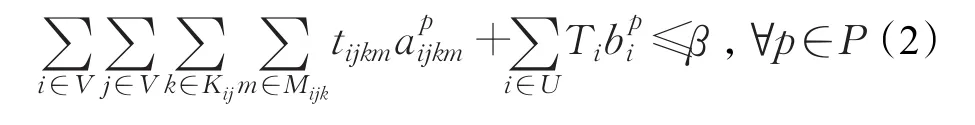
式（2）要求所有供需点对的配送时间不大于β，其中包括处理时间和运输时间。

（3）配送路径的连通性约束

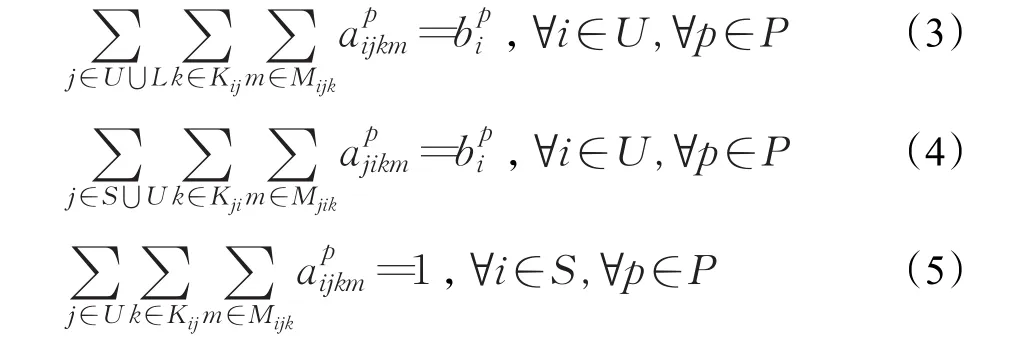
表2 决策变量

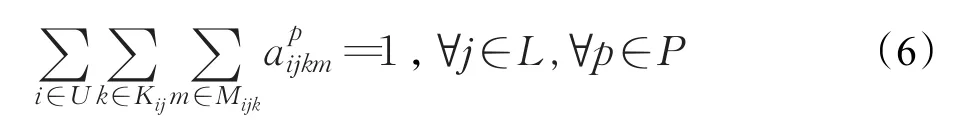
约束式（3）和式（4）表示如果3PL服务节点被选择服务于供需点对p，则必须有与其连接的3PL运输供应商的一种运输方式被选择来运出和运入产品；否则，没有3PL运输供应商或运输方式被选择；约束式（5）、（6）分别要求供需点对p的供应点和需求点必须通过3PL运输供应的某种运输方式来运出和运入产品。

（4）能力约束

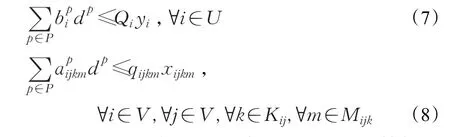
式（7）和（8）分别为3PL服务节点和3PL运输供应商某种运输方式的能力约束，并要求被选择服务于供需点对之间配送路径的3PL服务节点和3PL运输供应商的某种运输方式必须是已开设的。

（5）决策变量约束

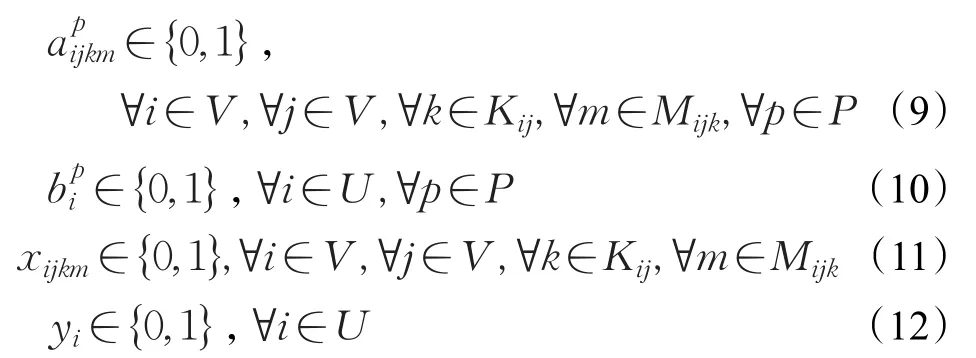
式（9）～（12）表示二值的0-1决策变量。

3 算法设计

考虑多种运输方式的4PL多到多网络设计问题是传统设施选址问题的扩展，因此也是NP-hard问题。在问题规模较大的情况下，求解很困难，所以智能优化算法更适合对该问题进行求解。本文设计混合蛙跳算法对问题进行求解。

混合蛙跳算法将种群个体视为青蛙，整个种群由多个子群构成。子群中个体进化是通过青蛙的三次跳跃操作更新实现的。目前，SFLA已经得到一定的研究[9]，并在图像分割[10]、作业车间调度[11-12]、车辆路径[13]、光伏模型识别[14]、电源规划[15]、云资源配置和工作流调度[16]、无线传感器网络节点三维定位[17]等问题中得到应用。

本文根据问题的特点设计SFLA进行求解，通过向量对青蛙个体进行编码。同时，为了满足配送路径的连通性约束，分别设计初始种群生成方法和青蛙的跳跃操作。

3.1 混合蛙跳算法步骤

混合蛙跳算法步骤如下：

步骤1生成含有F个青蛙的初始群体Pop0={X1,X2,…,XF}（详见3.3节），并按3.5节方法计算青蛙（解）Xi的评价函数值 f( )Xi。

步骤2将群体划分为M个族群，Pop={P1,P2,…,PM}。将青蛙按照评价函数值从小到大排序，并依次逐一循环分配给M个族群，每个族群Pk由N个青蛙组成，即

步骤3对每个族群执行深度局部搜索，具体过程如下：

重复上述过程，直到达到设定的更新迭代次数。

步骤4将所有族群的个体混合，确定全局最好个体；如果满足终止条件，则执行步骤5，否则，转到步骤2。

步骤5输出最好解。

3.2 个体的编码与解码

青蛙个体可由一组向量来表示。向量的数量为供需点对的数量。每个向量表示供需点对之间的一条路径。如图2所示，每个向量由三部分组成，其中第一部分表示节点的选择情况，每一位表示路径可能经过的节点（需求点除外），取值为“0”表示该节点没有在路径上，取“非0”值表示该节点在路径上，并且下一个节点为其值对应的节点；第二部分表示路径可能经过的节点之间3PL运输供应商的选择情况，“0”表示没有供应商被选择，“非0”表示其值对应的供应商被选择；第三部分表示运输方式的选择情况，每一位表示某两个节点之间3PL供应商的运输方式的选择情况，“0”表示没有运输方式被选择，“非0”表示其值对应的运输方式被选择。值得注意的是，因为不同的供应点或需求点与3PL服务节点之间的连接情况不同，所以不同路径所对应的向量维数可能不同。

图2 个体向量的表示

根据上述编码规则，给定向量的取值可以唯一确定对应的路径，进而可以确定变量和的值，再由约束式（7）和式（8）即可确定解 xijkm和 yi。

3.3 初始种群的生成

按照3.2节中青蛙个体的编码方式，随机生成初始种群。为了满足路径的连通性约束式（3）～（6），按照下列步骤产生个体的向量：

步骤1生成向量的节点部分。从供应点vs对应位开始，依次随机确定路径经过的节点及节点对应位的数值。如果某节点的下一个节点都已经是路径上的节点，则返回到供应点，并重新确定节点部分，直到到达需求点vl。如果某节点的下一个节点包含需求点，则其对应位的取值为需求点。

步骤2根据路径经过的节点顺序，依次随机选择3PL运输供应商，确定对应位的值。

步骤3根据3PL供应商的选择情况，依次找到被选择3PL供应商的对应位，并随机选择运输方式，确定对应位的值。

3.4 跳跃操作

青蛙在1次和2次跳跃过程中，根据族群Pk最差个体与族群最好个体（或全局最好个体）来产生新个体。在产生新个体的过程中，为了满足路径的连通性约束式（3）～（6），新个体的第 p 个向量由个体与或的对应向量与（或按照如下步骤生成：

步骤1对于向量的节点部分执行交叉操作：从供应点vs对应位开始，根据路径经过的节点按式（13）依次执行节点对应位 j的交叉操作。在交叉过程中，如果与（或）中对应位的值为需求点，则取值为需求点；如果对应位的值分别为“0”和“非0”，则取“非0”值。如果中对应位的值为需求点，则停止交叉过程。

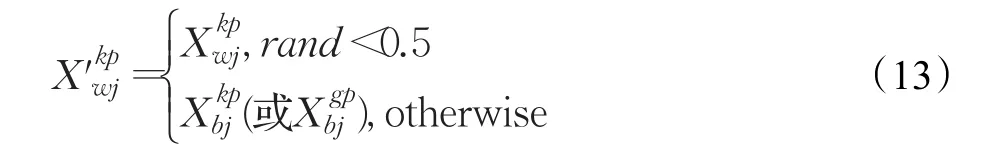
式中rand表示[ ]0,1之间随机数。

步骤2根据路径经过的节点次序，按照式（14）确定3PL运输供应商部分对应位 j的值。设路径经过的某两个节点之间有ξj个3PL运输供应商，那么对应位的取值范围为 1,2,…,ξj。如果中对应位的值小于1，则取1；如果对应位的值大于ξj，则取ξj。式中，round表示四舍五入取整。

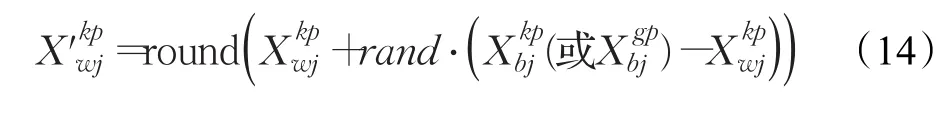
步骤3根据路径经过的节点次序和被选择的3PL运输供应商，再按照式（14）确定运输方式部分对应位的值。设路径选择的某个3PL运输供应商提供的运输方式数量为τ，那么对应位的取值范围为1,2,…,τ。如果中对应位的值小于1，则取1；如果对应位的值大于τ，则取τ。

3.5 个体的评价

通过对个体Xi解码得到(X ,Y )，并按式（15）对个体进行评价：

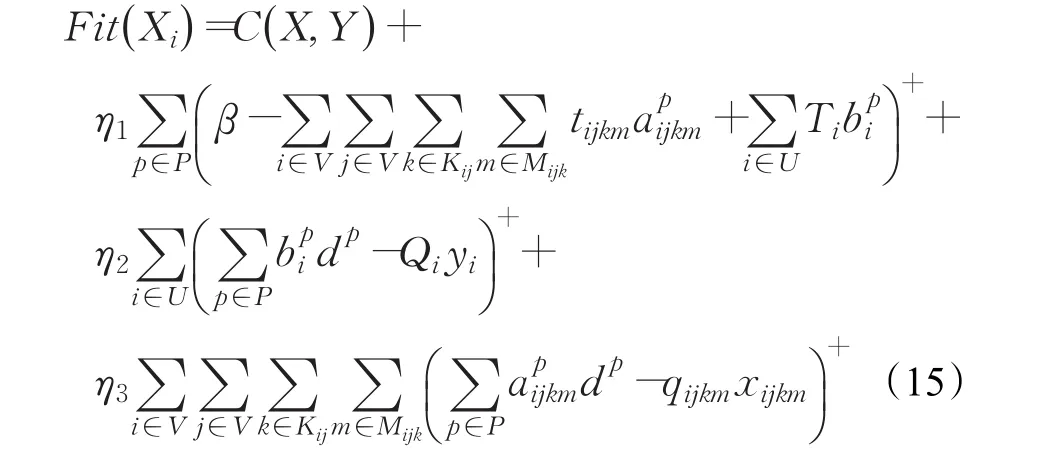
式中，C( )

X,Y 为目标函数式（1）。因为一个解还可能不满足时间约束式（2）和能力约束式（7）和（8），所以将其作为惩罚项加入评价函数中，η1为时间约束的惩罚系数，η2和η3分别为3PL服务节点和3PL运输供应商的能力惩罚系数。表示：如果括号内值为正，则取该值。

4 实验及结果分析

为了对模型的合理性及算法的有效性进行验证，对数据随机产生的算例进行测试。模型和算法均采用Matlab语言编码实现，并在Intel Core i5 CPU 2.20 GHz，内存4 GB的PC机上进行实验。

不同算例的规模如表3所示，包括供需点对的数量，3PL服务节点的数量和3PL运输供应商及运输方式的数量。算例的参数都按照下面均匀分布随机产生：供需点对之间的产品流通量；3PL服务节点的处理成本、处理时间、处理能力、开设成本。3PL运输供应商的运输成本、运输时间、运输能力、开设成本。其中，考虑公路、铁路、水路和航空四种不同运输方式，各种运输方式的参数取值如表4所示。

首先，对不同规模的算例进行求解，每个算例SFLA分别运行20次，并与遗传算法（GA）进行比较。SFLA的参数设置如下：族群数M为20，族群规模N为10，族群内局部搜索次数为10，总循环代数为100。为了公平比较，两种算法评估相同数量的个体，采用相同的编码方式和初始种群生产方法。GA算法采用基于轮盘赌的选择策略，采用基于路径的多点交叉策略，并通过随机改变路径的节点、3PL运输供应商或运输方式来实现变异策略。GA的参数设置如下：种群规模为40，循环代数为500，交叉率为0.5，变异率为0.2。表5给出算法求解的最好值、最差值、平均值和平均偏差率（（平均值－最好值/最好值）×100%）。由表5可见，对于不同规模的算例，SFLA的性能指标都优于GA，并且平均偏差率在0.3%～13%之间变化。表明SFLA能够对不同规模的算例进行有效求解并保持稳定的性能。

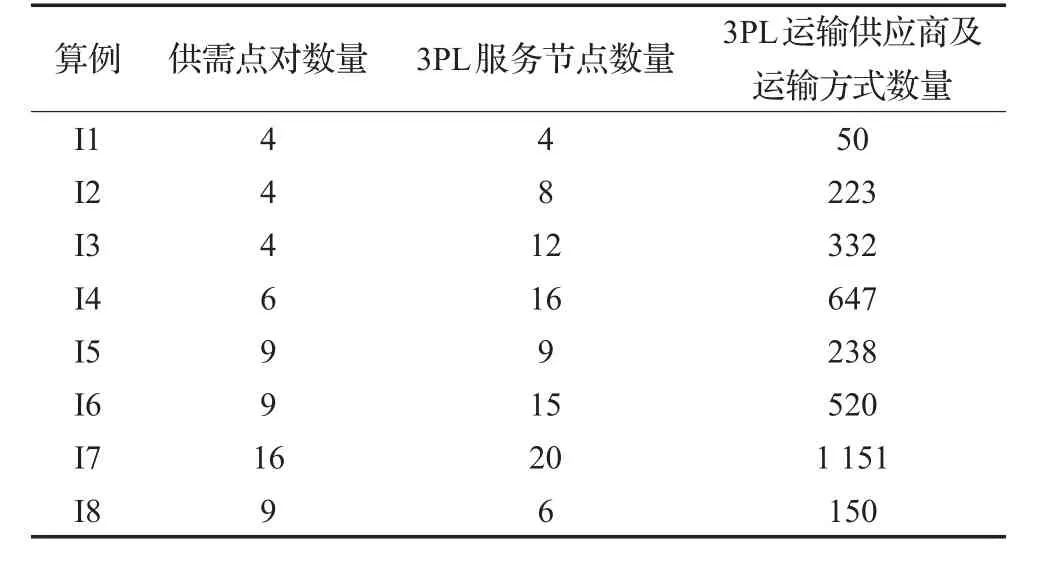
表3 算例的规模

表4 不同运输方式的参数取值

对不同配送时间约束下的算例I8进行求解，每个时间约束SFLA和GA分别运行20次。表6给出不同时间约束下两种算法的运行结果。由表6可见，SFLA的平均偏差率在1%～6%之间，并且各性能指标优于GA，表明SFLA在不同的配送时间约束下仍然能够保持性能稳定。

表7给出算例I1～I3的详细结果，包括总成本、开设成本、运输和处理成本、供需点对之间的配送路径和供需点对的配送时间。其中“Path1：1—（1，3）—5—（1，4）—7”表示供需点对1和7之间的路径Path1，该路径经过3PL服务节点5，并且选择节点1和5之间的3PL运输供应商1的水路方式以及节点5和7之间的3PL运输供应商1的航空方式进行运输。“s-d-1：16.7”表示第1个供需点对之间的配送时间为16.7（天）。

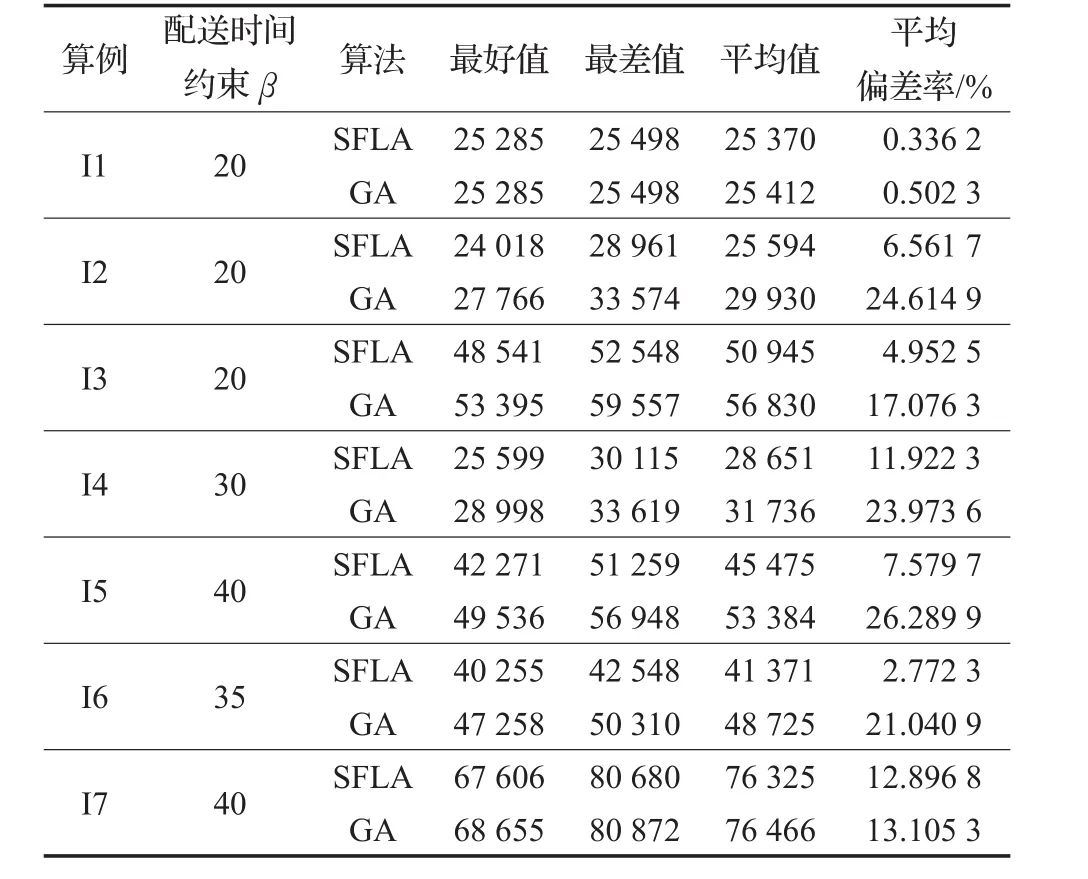
表5 SFLA和GA求解不同规模算例结果

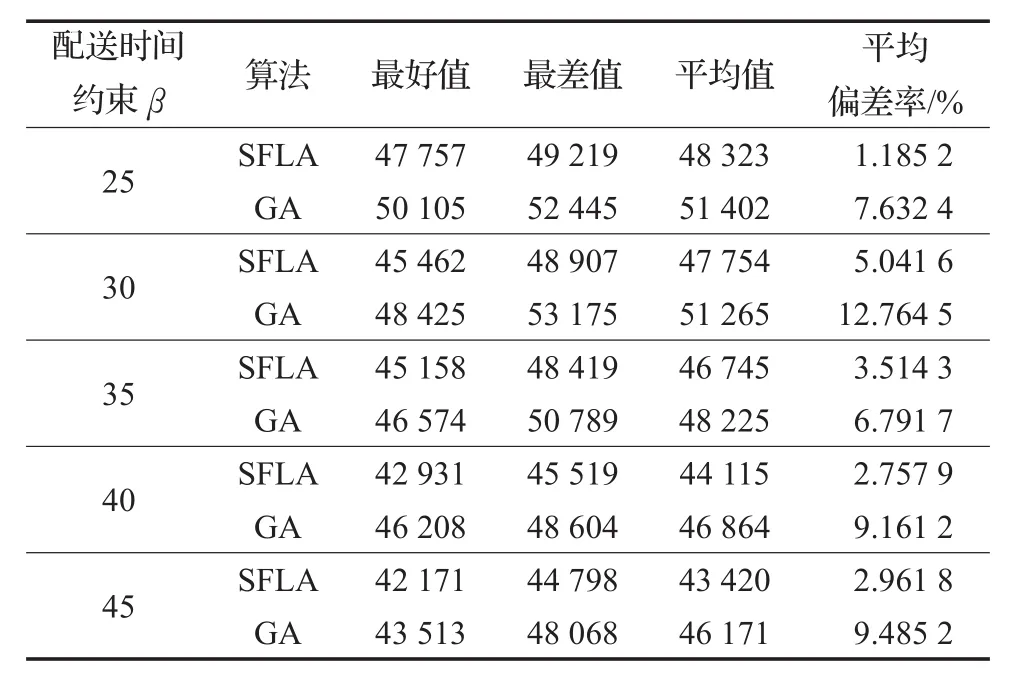
表6 SFLA和GA求解不同时间约束下算例I8的结果

表8给出不同配送时间约束下算例I8的详细结果。由表8可见，随着时间约束β的增加，总成本减少，运输和处理成本减少。因为，当配送时间约束增加，可通过开设具有较低处理成本的3PL服务节点和较低运输成本的3PL运输供应商及运输方式来构建符合配送时间约束的配送线路来完成配送任务。这可能导致配送线路的运输和处理成本降低，进而总成本减少。

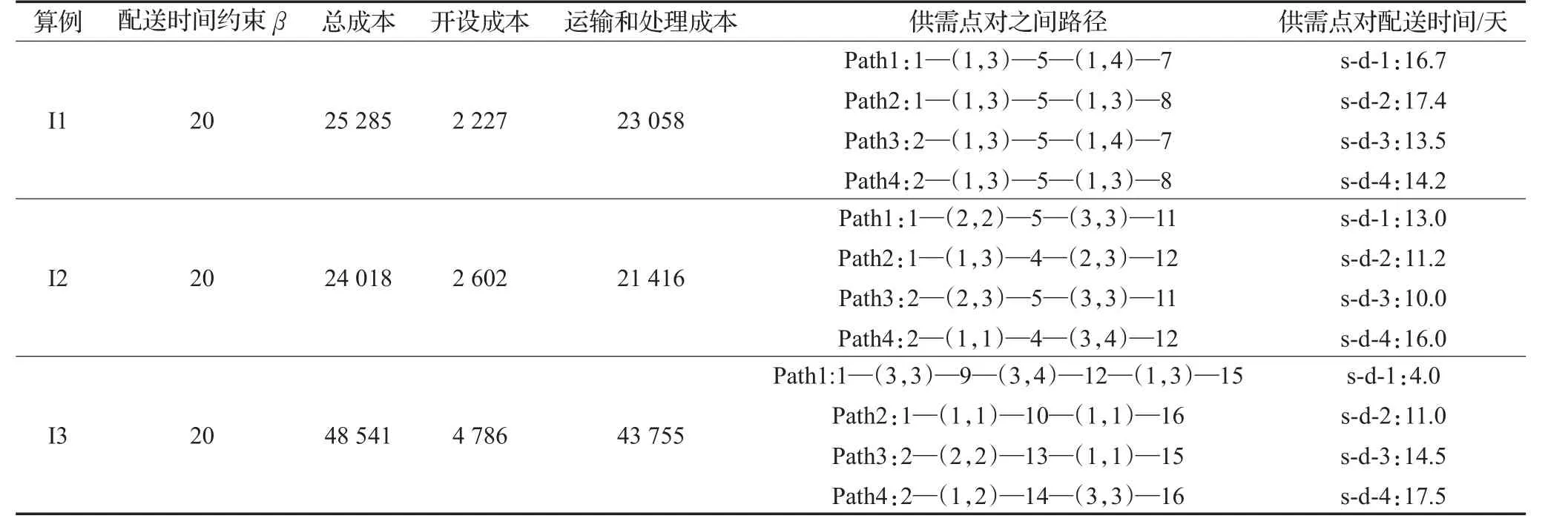
表7 不同规模算例的详细结果

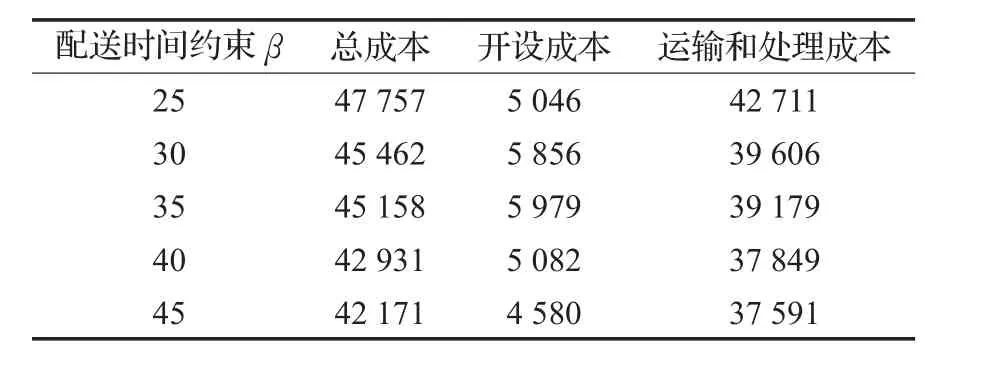
表8 不同时间约束下算例I8的详细结果

5 结束语

在考虑多供需点对之间配送和多种运输方式的情况下，为了获得高效运作的4PL服务网络，研究多种运输方式的4PL多到多网络设计问题。建立以总成本为目标，并满足配送时间约束的数学优化模型。针对问题模型特点，设计SFLA进行求解。最后，通过仿真算例来验证模型的合理性及算法的有效性。实验结果表明模型能够对问题合理描述，并且SFLA对不同规模和不同配送时间约束下的算例都能够有效求解并保持性能稳定。而且，随着配送时间约束参数的增加，运输和处理成本将减少。