基于GEP算法的高阶常微分方程预测模型

崔 未，王卫华，黄樟灿，谈 庆

武汉理工大学 理学院，武汉 430070

1 引言

随时间变化的动态系统在日常生活中广泛存在，如温度变化、降水量变化、金融数据变化等。如何对随时间变化的动态系统建模完成预测，一直是研究的热点。合适的时间序列模型对投资风险把控、投入产出评估等方面具有重要意义。

时间序列预测是一种根据现有数据的规律信息构建模型，并将模型外推来完成预测的方法。预测效果主要受模型选择影响[1]，这是由于时间序列数据是一个无显著规律的动态系统，数据随时间波动变化规律复杂，不同模型对数据的处理、构建联系和规律发现的方法有很大区别，使得模型对历史数据的描述有不同程度的偏差，进而对预测结果有直接影响。针对随时间变化的动态系统采样数据，通常采用ARIMA模型与人工神经网络（ANN）模型进行预测。ARIMA模型是一类线性模型，对非线性问题处理能力较差。为提高它的非线性能力，文献[2-5]将ARIMA模型与深度信念网络、支持向量机和GARCH等模型结合，在红潮预测、铀矿价格预测、网络流量预测和地铁乘客量短期预测等方面取得了一定的效果。虽然上述方法使得ARIMA模型在许多非线性系统预测问题中得到了运用，但是ARIMA模型对数据平稳性要求高，对非线性数据规律的捕捉能力较弱的问题依旧存在。与ARIMA模型及其改进相比，ANN有更强的非线性能力和自适应能力，对复杂非线性数据的规律发现能力更强，但它存在对数据数量要求高、参数设定复杂和模型解释性差的缺陷[6]。对此文献[7-11]采用PSO、GA等优化算法对BP神经网络和RBF神经网络进行参数优化；文献[12]将前馈神经网络（FNN）嵌入到EMD预测框架中，利用EMD框架的加权重组策略对FNN进行赋权，实现了FNN参数的自适应；文献[13]中将改进小世界网络应用到Leaky ESN中，在实现稀疏连接的同时，改善了神经节点的连接方式，提升了Leaky ESN的适应性，取得了更高的预测精度。虽然这些混合算法对参数设定复杂、数据量要求高的问题进行了解决，在一类时间序列预测问题上取得了良好效果，但是它们本质上是一个无显式模型的“黑盒”，对模型输出缺少合理解释，对模型的进一步分析研究存在阻碍。

为了弥补这些模型具有“黑盒”性质的缺陷，研究人员提出通过符号回归，以代数形式构建微分方程模型。基于演化算法的常微分方程建模方法早在2000年就被提出[14]，该方法在建模过程中分为两步，首先使用遗传规划（GP）构建模型，接下来通过遗传算法（GA）对模型进行参数优化。由于GP的遗传操作是基于树结构进行的，因此在建模过程中，存在容易陷入局部最优的问题。除此之外，受制于两步建模以及当时的计算条件，进行一次成功建模需要50 min，因此该方法虽然在预测精度上表现较好，但是未得到广泛应用和推广。

基因表达式编程（GEP）是一种融合了GA与GP优点的新型演化算法，寻优效率比二者高出100～60 000倍[15]。这是因为GEP对表达式树结构的更改通过对线性编码的修改完成，相比GP对树结构直接进行修改有更高的灵活性，种群多样性更丰富，能够有效地在保证精度的前提下提升建模效率。

综上，为了提升演化算法在常微分方程建模中的效率，改善人工神经网络等非线性方法在时间序列预测建模中无法获得显式模型和精度较低的缺陷，本文提出基于GEP的高阶常微分方程建模方法，并对太阳黑子年平均数进行建模预测。

2 基因表达式编程（GEP）

葡萄牙科学家C.Ferreira结合了遗传算法（GA）和遗传程序设计（GP）的优点，于2001年提出了基因表达式编程（GEP）[16]。GEP是一种拥有“基因型-表现型”特性的遗传算法，即采用固定长度的线性编码，对线性编码使用遗传算子进行操作，通过“Karva”语言将线性编码转化为表达式树（ET），树结构最终转化为表达式。下面对GEP编码及操作进行详细介绍。

2.1 GEP编码说明

GEP对染色体通过遗传操作完成进化。染色体由基因通过连接函数构成。染色体是由函数集F和终止集T构成。函数集包含基本初等函数、逻辑运算符和变量；终止集T中有且只有变量及参数。基因分为头部和尾部两部分，头部由函数集F与终止集T构成，尾部由终止集T构成。尾长度由头长度决定，关系式为：

其中t为尾长度，n为运算符目数，h为头长度。下面以一个例子对GEP的编码进行说明。

形如“Q+*/aaaba//+//sin+abababa”的线性编码对应的表达式为：

式（2）对应的表达式树和染色体编码如图1所示。

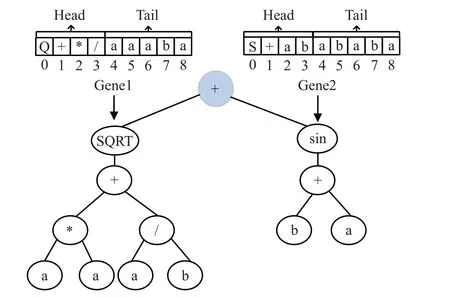
图1 式（2）对应的染色体编码与表达式树

从图1可以看出，该表达式通过两个等长基因构成的染色体表示，连接函数“+”将两个基因连接。基因的头结点长度为4，尾结点长度通过式（7）计算可知为5，总长度为9。基因1将尾部进行了部分表达，基因2对尾部没有进行表达。这种编码方式根据基因中符号集元素的分布情况，灵活地选择是否对基因全部进行表达，与GP直接对树结构操作相比更为灵活，与GA的二进制编码相比有更丰富的表现形式。

2.2 GEP基本流程

GEP在种群在进化过程通过对染色体进行遗传操作，使种群向符合适应度函数的方向进化[17]。GEP的操作流程如图2所示。

对图2进行总结，得到GEP的操作流程如下：

步骤1根据设定参数进行种群初始化。

步骤2计算种群适应度，判断是否达到结束条件，是则跳出循环，否则进入步骤3。

步骤3进行遗传操作。

步骤4得到一组新解，返回步骤2。

图2 GEP操作流程图

通过上述流程完成模型建立。下面对GEP的遗传算子进行简单介绍，遗传算子包括选择复制算子、转座算子、重组算子和变异算子，四种算子及操作方法如下：

（1）选择复制算子：GEP中采用基于精英策略的轮盘赌选择，即对适应度最高的个体进行保留并复制，其余个体的选择通过轮盘赌进行。

（2）转座算子：转座是指染色体中的基因片段能够转移到该染色体或其他染色体的各个位置。转座根据转移目标的不同，分为IS转座、RIS转座和基因转座。

①IS转座：选择带有运算符的基因片段，将该片段插入到基因的头部中（除了起始位置以外的任意节点）。

②RIS转座：从头部开始选择一个基因片段，从片段中选取第一个可以表示完整函数的部分作为RIS片段，将该片段插入到基因的尾部中。

③基因转座：将整个基因插入到染色体的起始位置，染色体长度保持一致。

（3）重组算子：重组根据基因片段截取方式不同分为单点重组，两点重组和基因重组。

①单点重组：父代染色体配对，确定截断点，将截断点后的部分进行交换。

②两点重组：父代染色体配对，通过两个阶段点确定截取片段，对截取片段进行交换。

③基因重组：父代染色体配对，对选中基因进行交换。

（4）变异算子：变异算子是最高效的遗传算子，变异可以发生在染色体的任何位置。在头部中的运算符和终止点均可以通过变异相互转换。尾部的终止点只能进行终止点变异。

染色体经过遗传操作，不断迭代，最终得到适应度最高的个体，即为最优解。下面对基于GEP的高阶常微分方程建模进行详细介绍。

3 基于GEP的高阶常微分方程预测模型

3.1 数学方法说明

针对一组动态系统观测样本：

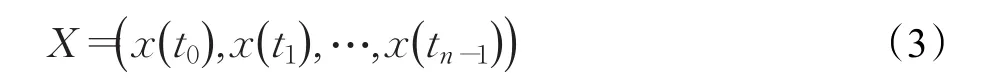
对这组数据进行预测的方法是通过不同方法对这组数据进行规律挖掘，建立模型 f如下：

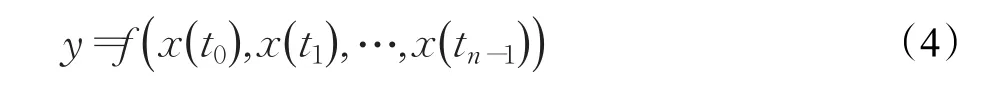
通过 f进行n步外推，对后n个时刻的数据进行预测。常见的动态系统大多为非线性系统，如股票价格、温度变化和太阳黑子变化等。它们都是非线性、非平稳、复杂度高的时间序列数据，对数据规律的发现和总结存在较大难度，因此以人工神经网络为代表的非线性建模方法在这类数据的预测上得到了广泛应用。但是这类方法的问题在于它们所建的模型 f是一个隐式模型，只能通过对参数的修改完成对模型的改进，无法对模型进行更为深入的研究。为了改善这个缺陷，本文利用常微分方程对动态系统准确描述的特性，构建高阶常微分方程模型 f并完成预测。对X构建高阶常微分方程的主要步骤如下所述：

对于规模为n的动态系统X进行m阶差分近似，得到矩阵 Mn×m：

通过矩阵M中的元素，对X进行高阶常微分方程建模得到：

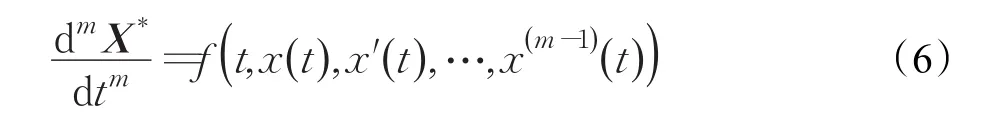
使得：

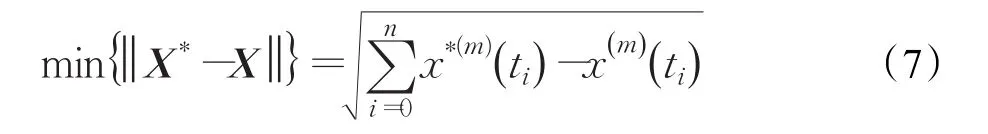
成立。其中左边部分具体为：

其中，n代表数据规模。对式（6）进行数值求解，得到接下来τ步的预测值：

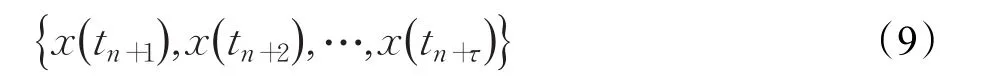
式（6）中，f是由符号回归而成的。基于GEP的高阶常微分方程演化建模，即通过对规模为n的连续观察数据进行差分处理，利用GEP的自组织、自学习的特点对已处理数据进行建模，得到形如式（6）的表达式。下面对上述步骤分别进行详细说明。

3.2 有限差分

为了得到数据波动规律，首先需要对数据进行有限差分处理，计算导数近似值[18]，构建矩阵M。以一阶导数为例，通过下面的数值差分公式得到导数近似值。

对t0时刻的数据进行如下处理：

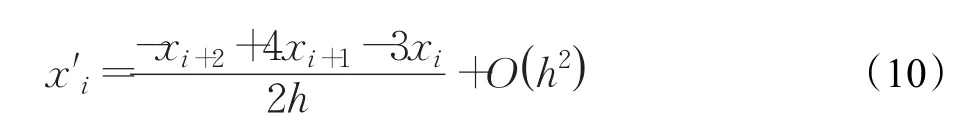
对t1～tn-3时刻的数据进行如下处理：

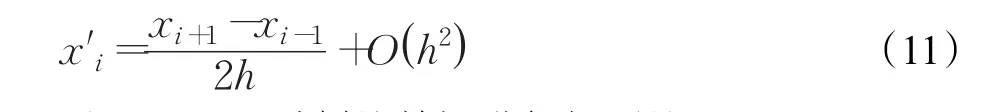
对tn-2～tn-1时刻的数据进行如下处理：

其中，h代表单位时间间隔，xi代表i时刻的数据。更高阶的计算以此类推，保证不同时刻的数据误差始终为O(h2)。

3.3 GEP-HODE算法

通过有限差分得到矩阵式（5），使用GEP对M 构建如式（6）所示函数关系 f，整体流程如图3所示。

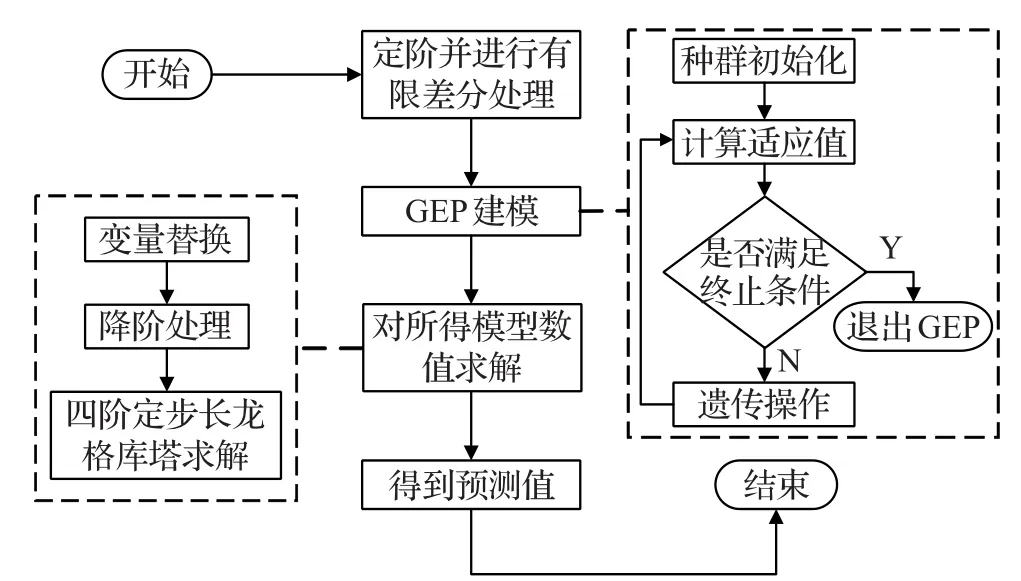
图3 GEP-HODE算法流程图

根据图3，对算法步骤进行归纳，具体流程如下：

输入：时序数据X，时间t。

输出：高阶常微分方程模型 f。

步骤1输入HODE模型阶数m。

步骤2计算m阶导数近似值，得到矩阵M。

步骤3确定迭代次数并对GEP进行参数设定。

步骤4进行种群初始化，并计算适应度。

步骤5对种群进行遗传操作，形成新种群。

步骤6根据迭代次数判断是否结束运算，是则结束，否则返回步骤2。

步骤7根据GEP建模得到模型 f。

步骤8利用数值方法对 f进行求解，得到最终预测值。

3.4 适应度函数选择和模型求解

3.4.1 适应度函数选择

模型的建立是通过GEP以适应度函数为目标演化进行的，因此适应度函数的选择对模型的构建有直接影响。GEP-HODE模型是以式（7）为评判标准的，即向模型拟合值与实际值误差最小的方向进化。标准绝对误差函数的作用与式（7）相同，故本文选择该函数作为适应度函数，如式（13）所示：

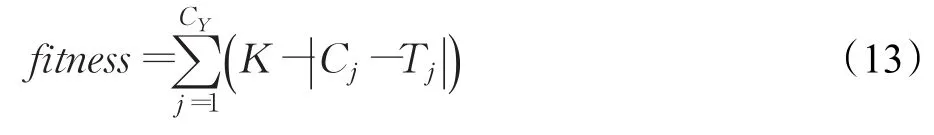
其中K为选择范围，一般情况下选择1 000。CY为样本数，Cj为模型所得，Tj为目标值。

3.4.2 模型求解

由GEP-HODE算法得到的高阶常微分方程模型是一类非线性模型，因此常采用数值解法进行求解。这种方法的思路是将高阶方程转换为多个一阶方程构成的方程组，利用数值方法对一阶方程逐个求解，利用所得结果进行递推，进而得到高阶方程的数值解。针对式（6）所示模型，首先进行如下变换：

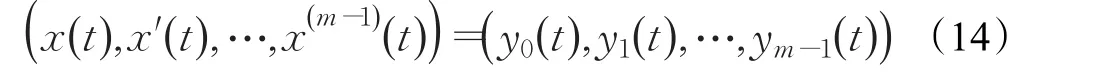
根据变量替换，将式（6）所示的高阶常微分方程转化为式（15）所示的常微分方程组：

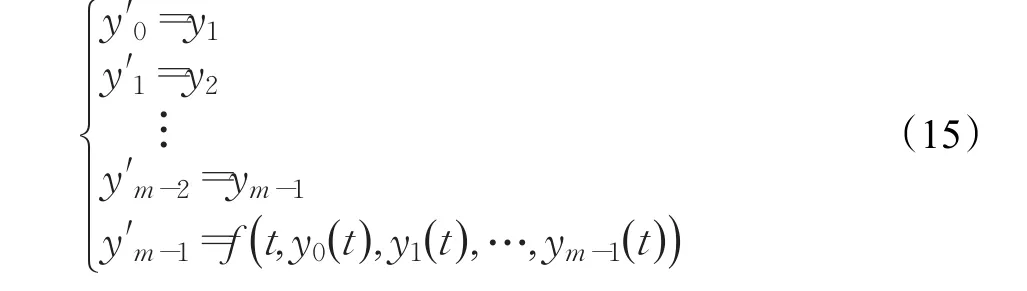
其中t表示t0～tn的所有时间节点。常微分方程组的初值为：

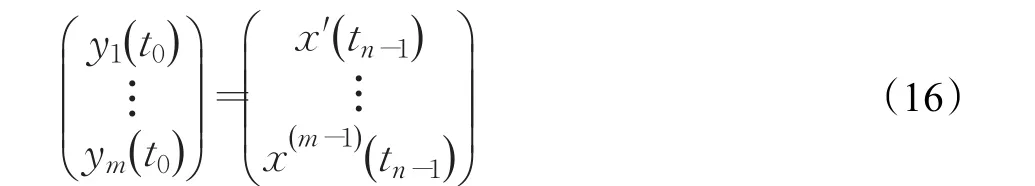
通过数值方法，对式（15）所示的方程组从下至上递归求解，最终得到预测值y0( )t+τ，其中τ为预测步长。

4 计算机建模与仿真

4.1 数据选择与参数设定

本文使用太阳黑子年平均数据[19]，设计实验进行对比分析。实验使用1749—1919年太阳黑子年平均数据，与文献[14]中所用数据一致。其中训练集为1749—1863年的数据，样本总数为115，测试集为1864—1919年的数据，样本总数为56。对1920—1924五年的太阳黑子年平均数进行预测，将GEP-HODE模型的预测结果与文献[14]中方法（下面称为GPGA方法）、SVM-ARIMA模型[20]、PSO-BP神经网络模型[21]和单因素GEP预测模型进行结果对比分析。数值解法采取步长为0.1的四阶龙格库塔算法，初值为最后一个数据点对应的值。参数设定表如表1所示。

4.2 误差评判标准

本文选取的误差评判标准为平均绝对误差MAE、平均绝对误差百分比MAPE和均方误差RMSE。平均绝对误差用来衡量预测值与实际值的直接差距；平均绝对误差百分比用来衡量预测值相对实际值的变化情况；均方误差用于判断预测值中是否有偏离实际值较大的点。它们的计算公式分别为：

表1 参数设定表

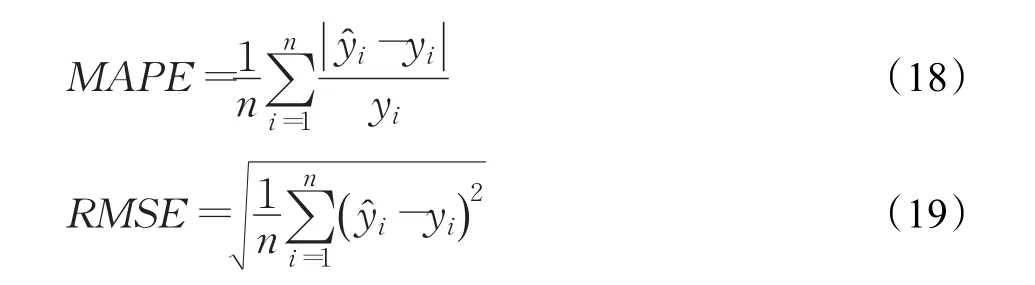
4.3 实验结果与对比分析

1749—1919年的太阳黑子年平均数量样本共171个，样本按年分布如图4所示。

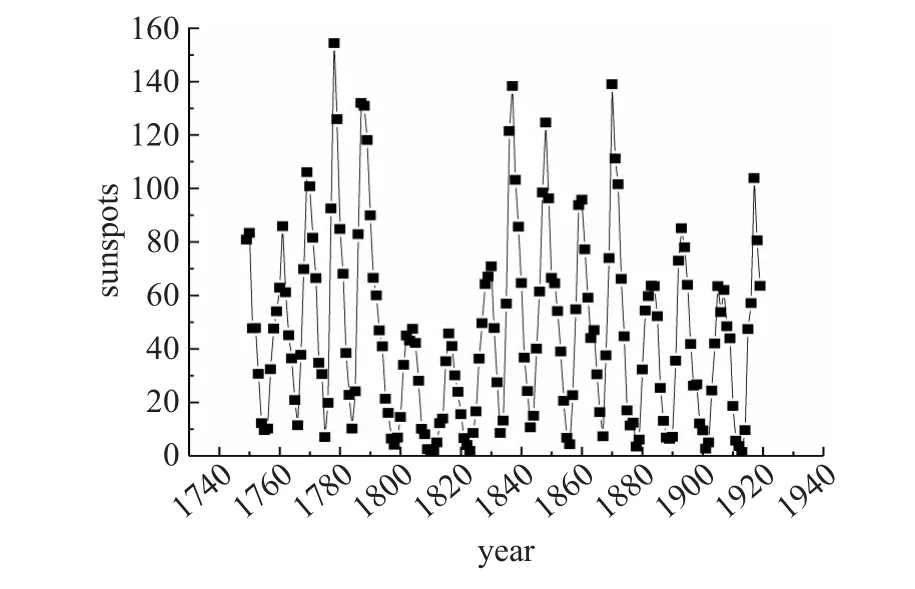
图4 1749—1919年太阳黑子年平均数目分布图

从图4中可以看出太阳黑子年平均数据是一组非线性、非平稳的时间序列数据，没有明显的变化规律。采取GEP-HODE方法进行常微分方程建模，得到1～4阶模型。每阶模型进行五次建模，取预测误差平均值进行分析，各阶模型预测误差对比如表2所示。

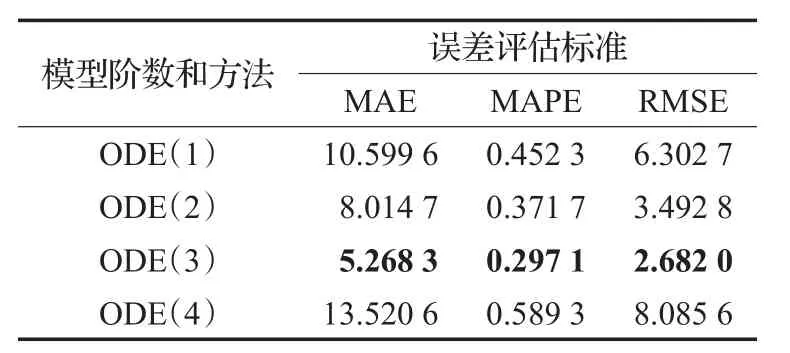
表2 各阶模型预测误差对比表

从表2可以看出在三种误差评判标准下，三阶常微分方程模型（ODE（3））在对太阳黑子年平均数据建模预测效果最好。效果最好的ODE（3）模型如下所示：

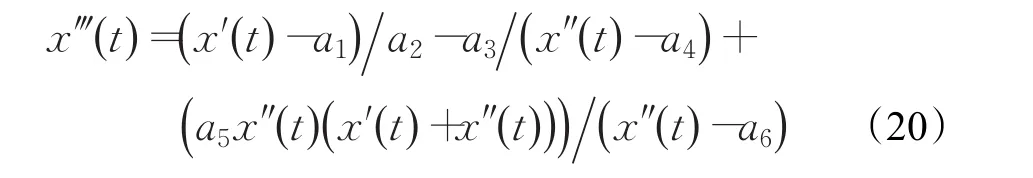
模型参数如下：

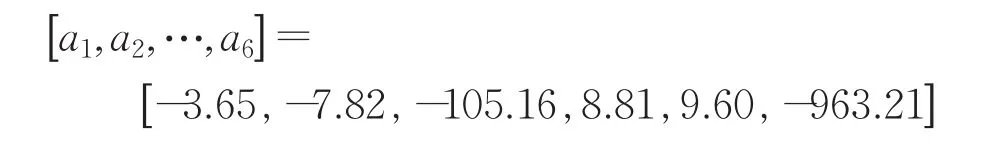
为了体现GEP在建模中的高效性和模型的精确性，下面将式（20）所示模型（下面称为GEP-HODE模型）与GPGA等四种方法进行对比。预测精度结果如表3所示。

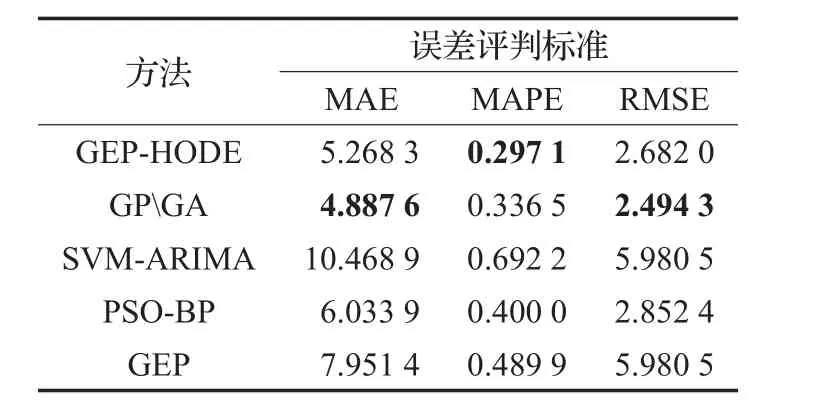
表3 预测结果误差对比表

从表3中能够看出GEP-HODE模型的预测误差在三种评判标准上均小于后三种预测模型，在MAE与RMSE上低于GPGA方法，在MAPE上高于GPGA，总体预测结果较为接近，下面对造成这种结果的原因进行分析。太阳黑子年平均数是一个随时间剧烈变化的非线性动态系统，ARIMA本质上是一个线性模型，即使通过SVM将数据映射到高维空间试图削弱非线性造成的影响，也无法获得更为准确的预测结果，同时SVM的参数设定以及径向基函数的选择也较为主观，因此SVMARIMA模型预测结果在五种方法中最差；单因素GEP预测模型的问题在于其本质上是一高阶复合函数拟合模型，由于数据维度为1，因此该模型对数据的规律总结能力与微分方程模型相比较弱，但与ARIMA相比，它的非线性能力更强，因此该模型的预测结果相较SVMARIMA模型更好；BP神经网络尽管通过PSO算法对各连接层的权值进行了优化，但数据量较少、隐藏层数人为设定等问题使得模型训练效果较差，导致预测精度较低，但是该模型出色的非线性能力使得它在常微分方程模型之外的三种对比方法中精度最高；GEP-HODE与GAGP预测误差相近是因为二者同属于对常微分方程的演化建模，因此它们本质上是一致的。由于使用的演化算法不同，导致了它们的结果虽然相近，但是仍然存在着一定的差异。因此需要对造成这种差异的原因进行进一步分析。

首先对两种方法的预测结果进行对比，如图5所示。

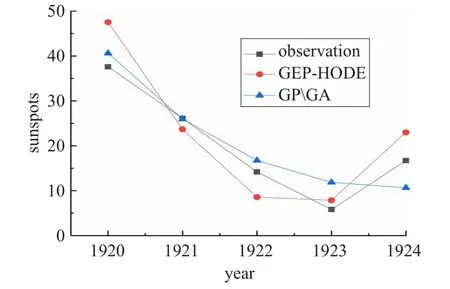
图5 两种方法预测结果对比图

从图5可以看出GPGA方法在整体数据点的数值预测上精度要略高于GEP-HODE方法，从表3中则可以发现二者在预测误差上相差不大。作为一种预测手段，对数据趋势的预测也属于模型预测能力的一部分，从图5中可以看出GPGA方法在1923—1924年这一段的预测与实际趋势完全相反，而GEP-HODE方法则准确地反映了这段时间的实际情况。因此，虽然二者在精度上是比较接近的，但从预测图像上来看，GEP-HODE方法相较GPGA方法表现更好。从理论上看，二者均属于遗传算法，在模型表达方面和遗传操作方面十分类似，因此得出的数值解精度也十分相近。导致预测趋势产生偏差的原因在于GPGA方法通过GP进行模型建立，利用GA进行参数优化，这种方法受制于GP的编码结构，导致模型结构存在一定的缺陷。详细的说，由于GP在进化过程中通过对树结构进行变换和修饰，实现遗传操作获得新解，这种操作方式会导致解的多样性不足，因此GP容易陷入局部最优。GEP算法改进了编码方式，将遗传操作应用在线性编码中，通过表达式树对遗传操作进行体现。这种“基因型-表现型”的操作方式丰富了解的多样性，相较GPGA方法跳出局部最优的能力更强，因此在模型的建立方面相较GPGA存在一定优势，使得预测趋势更为精确。

接下来对两种方法的建模效率进行对比。两种方法在函数集相同、连接函数相同、迭代次数相同以及同一环境下（intel core i5 4200h）重复进行五次，将两者用时进行对比。对比结果如表4所示。

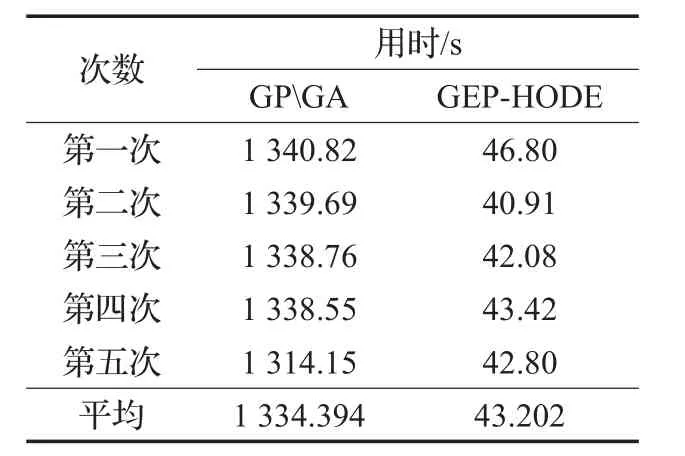
表4 建模用时对比表

从表4中可以看出五次实验GEP算法的效率远高于GPGA方法。一方面因为GEP通过改进编码方式，从本质上比GP的进化效率高；另一方面由于GPGA属于混合算法，在建模过程中首先需要通过GP进行模型建立，随后需要通过GA进行参数优化，“两步走”的建模过程导致了运算时间的增加。与之相比，GEP一方面将模型建立与参数优化同时进行，另一方面采取了更为高效的编码方式，因此用时更短，效率更高。

综上，GEP-HODE方法在具有代表性的太阳黑子年平均数据预测上取得了一定的成果，与改进人工神经网络模型和混合ARIMA模型相比具有更高的精度，能够在保证预测精度的同时能够获得显式模型的优势；与GPGA混合建模方法相比拥有更高的效率，具备更优秀的趋势预测能力。如何通过减小导数近似带来的误差以及对GEP算法进行改进，提高模型对历史数据的描述能力，从而进一步提升模型精度是接下来要研究的问题。

5 结语

本文针对动态系统预测建模问题中存在的建模效率低和无显式模型的缺陷，提出了一种基于GEP的高阶常微分方程建模方法。该方法兼容了高阶微分能够对短期波动数据变化具有较强描述能力，能够深入挖掘数据本征的特点和GEP算法的自组织、自适应特性。具备高效率、高精度和拥有显式模型的优点。以不同时间段的太阳黑子年平均数为例构建模型，通过与GAGP、SVM-ARIMA、PSO-BP等方法进行对比，分析说明GEPHODE方法的优势以及造成其他方法出现误差的原因，最终结果表明GEP-HODE方法在精度和效率上分别具有一定的优势，可以对动态时间系统进行建模并完成预测。