穿刺机器人运动安全性的形式化分析与建模
2018-09-18孙浩然施智平
孙浩然,施智平,3,关 永,王 瑞
1.首都师范大学 成像技术北京市高精尖创新中心,北京 100048
2.首都师范大学 信息工程学院 轻型工业机器人与安全验证北京市重点实验室,北京 100048
3.北京数学与信息交叉科学2011协同创新中心,北京 100048
1 引言
混成系统(hybrid system)[1-2]是一种嵌入在物理环境下的实时系统,一般由离散组件和连续组件连接组成,组件之间的行为由计算模型进行控制。其中,连续组件一般通过系统变量对时间的微分方程来描述系统的实际控制模型以及系统中参数的演变规律;离散组件则通过状态机、Petri网等高抽象层次的模型来描述系统的逻辑控制转换过程。在两个部分之间,通过一定的接口与规则将连续部分的信号与离散部分的控制模式进行关联与转换。
随着科技的发展,人们对控制系统行为的需求变得越来越复杂,使得混成系统在工业控制中大量出现。特别是在安全攸关的系统中,例如:医疗设施、航空航天、交通运输等领域。同时,混成系统的失控所带来的灾难也越来越沉重,例如飞机导航系统的失误导致机毁人亡,芯片的设计错误给公司带来几十亿美元的回收代价,医疗设备突然失控夺去病人的宝贵生命等等。因此,对混成系统的安全性验证已经成为一个亟待解决的问题。
近几十年来,形式化方法(formal method)[3-4]在很多领域中都取得了巨大进步,基础研究的进展加上技术进步的推动,使新方法和新工具不断出现并逐步完善成为一种成熟的高可靠验证技术。形式化方法是通过数学方法证明被验证系统满足系统规范。根据数学理论来证明设计的系统是否满足期望的性质,在不能证明期望的性质时,则可能发现设计错误。形式化验证正是通过这种方式增强了对系统的理解和增加了发现设计错误的机率。因此,本文将通过穿刺机器人的实例,使用形式化方法验证机器人运动控制系统的安全性。
形式化方法主要包括模型检验(model checking)[5]和定理证明(theorem proving)[6]两个方面。相较于模型检验通过遍历状态空间来证明性质的方法,定理证明主要采用逻辑和数学推理证明的方法验证关键性质。针对状态复杂的混成系统而言定理证明方法具有更良好的性能,并且已经取得了一系列的进展。
何积丰院士等人在CSP[7]基础上提出了混成CSP语言,可以用来描述组合混成系统。Sankaranarayana等人提出了生成混成系统不变式的方法[8],该方法利用约束求解的方法预先给出多项式模板,然后基于模板生成多项式不变式;詹乃军老师等人提出了一种通过李导数求解混成系统半代数不变式的方法[9]。此外,Barrier Certificate[10]是混成系统不变式生成方向上的又一个重要成果,Prajna提出了一种通过利用平方和(sum of square)与半定规划(semidefinite programming)技术来生成多项式不等式形式的混成自动机不变式的方法。
与以上方法相比,本文采用微分动态逻辑(differential dynamic logic)[11]的方法验证穿刺机器人的安全性,该方法被视为近期混成系统定理证明领域的重大突破。微分动态逻辑主要思想是:不求解微分方程,而是寻找这些微分方程的微分不变式(differential invariant)[12],从而避免了求解微分方程可能导致的不可控计算量问题。
2 案例分析
机器人辅助医疗技术[13]是现代外科医学的重要研究方向。研究机器人辅助穿刺技术的安全性不仅具有重要的理论价值,而且在临床上可以有效地提高穿刺的安全性和活性。
2.1 穿刺机器人控制系统
穿刺机器人[14]是现代外科手术中较为普遍的技术,特别是在微创外科领域。当前,穿刺术主要通过医生手工完成,其准确性和穿刺质量完全依赖医生的经验和能力。近十年来,机器人辅助技术在现代医学中的应用得到越来越广泛的认可。以da Vinci,ZUES为代表的外科手术机器人系统在临床上的成功案例吸引了医学界、科技界极大的兴趣。机器人辅助穿刺避免了医生直接暴露在射线下,同时克服了医生疲劳、手抖动和手眼协调问题等引起的操作误差,提高了穿刺的精准性和稳定性。同时,穿刺机器人在医疗环境中的安全性、可控性等问题也引起了人们的高度重视。
机器人辅助针穿刺系统主要有两类[15]:自主系统的安全性是本文讨论的重点,因为自主系统是机器人辅助穿刺的最终目标且面临的安全性问题更加严峻。穿刺针能否根据定位系统准确地自主运动到靶点位置,能否在提高穿刺效率的同时保证安全性等等都是将要验证的问题。本文不考虑机器人复杂的机构学设计,仅从末端执行器的运动学角度建模分析穿刺过程的安全性等问题。
穿刺是外科手术中常见的手术动作,可以根据操作环境和约束条件等因素将整体目标分为四个子目标,分别为加速运动(fast movement)、减速运动(slow movement)、垂直姿态(Perpendicular attitude)和穿刺(puncturing),如图1所示。
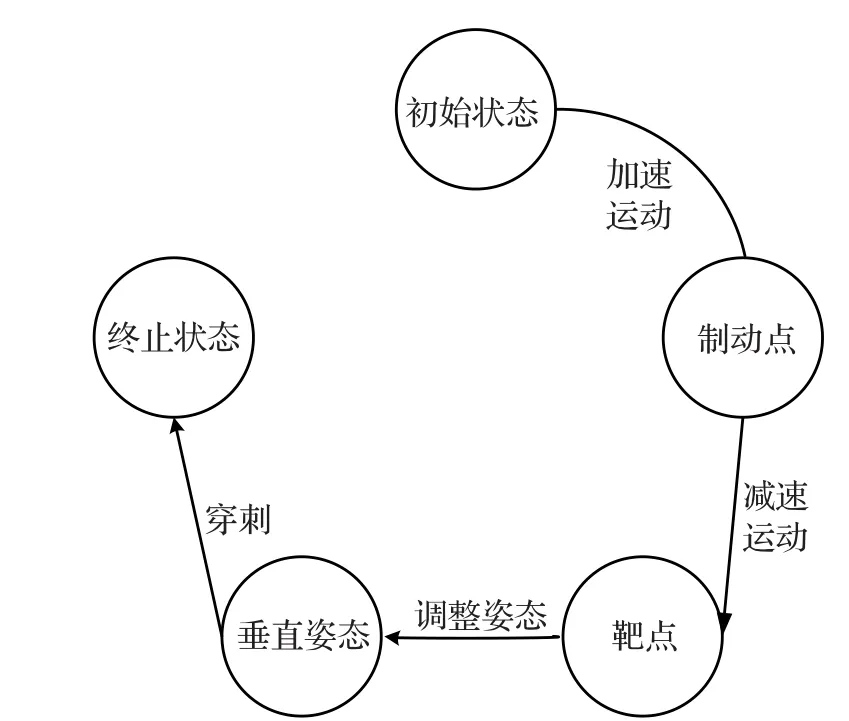
图1 穿刺运动过程
当末端执行器从初始状态出发后为了尽快到达靶点位置开始加速运动,在靶点附近到达某一制动点位置时开始减速运动,并最终在靶点位置处停止运动。之后调整穿刺针的姿态,当穿刺针姿态与靶点所在表面方向垂直时进行穿刺,到达终止状态时结束动作。
本文将着重讨论末端执行器在任意初始状态下以满足约束的任意加速度开始运动后,如何确定开始制动点的约束条件,保证末端执行器以满足约束的任意制动力开始减速并可以安全地停止在靶点位置。
2.2 微分动态逻辑
微分动态逻辑是建立在混成系统上的一阶逻辑,具有描述混成系统性质的能力,可以简洁地表达出混成系统的安全性等性质。微分动态系统的原理是在单个的形式化语言中将系统的操作及系统正确的状态声明结合在一起。允许系统操作α作为模态逻辑的动作,为动态逻辑提供形如[α]ϕ 和 <α>ϕ 的公式。[α]ϕ 表示系统α的所有运行状态均满足条件ϕ;<α>ϕ表示在系统α的所有运行状态中至少存在这样一个状态满足条件ϕ。在微分动态逻辑中,混成程序(hybrid programs)通常扮演α的角色。
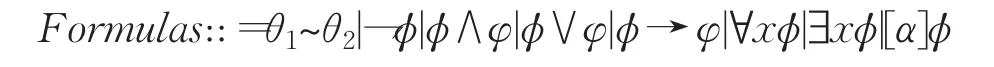
微分动态逻辑具有详细的推理证明演算法则,实质上是一种便于证明的标准逻辑公式。一般公式形如,前提条件为Γ,而结论为Δ。此公式的语义等同于证明演算是一种推理规则,可以推理出公式正确或错误的性质。微分动态逻辑规则是基于一阶逻辑规则的扩展,加入了针对量词消去、微分方程的替换规则,由于混合了的运算,需要消去这些运算从而转化为基本的一阶逻辑公式。例如公式(1)自底向上表述了离散过程中可以表示为在公式ϕ中将 xn替换成θn,从而消去了算子。
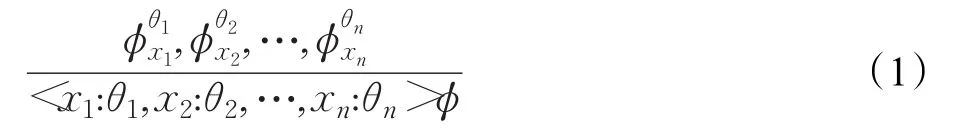
混成系统可以用混成程序(hybrid programs)来进行描述。混成程序是一种规范的应用于混成系统形式化的模型。混成程序可以将混成系统的离散跳转和连续演化相结合,实现既简洁又准确的形式化、结构化的控制。混成程序由三个部分组成:离散跳变集、微分方程系统和控制结构。离散跳变集包含了系统的离散变化,对状态变量(实质是微分方程中的变量)进行瞬时的赋值操作。微分方程系统表示了动态系统的连续性变化及其变化域。控制结构表示了离散和连续之间转移的关系,利用操作符可以连接不同的混成程序,实现了系统间的联系和交互。
下面是部分混成程序的表述形式以及对应的作用效果。
(1)x1:θ1,x2:θ2,…,xi:θi:离散的跳变集,同时将值θ1,θ2,…,θi分别赋值给 x1,x2,…,xi。
(2)x′1=θ1,x′2=θ2,…,x′i=θi& χ:连续演化过程。由项 θ1,θ2,…,θi组成的关于 x1,x2,…,xi的微分方程,并且带有一阶逻辑的限制条件x1,x2,…,xi。
(3)状态检测。检测当前状态的一阶逻辑范式χ的值是否为真。
(4)α;β:顺序组合。当α完成后再顺序执行β。
(6)α*:不确定性重复。重复执行n次α,n可以是任意自然数。
2.3 形式化分析与验证
穿刺机器人的安全性指运动过程中,末端执行器在满足约束条件(区域限制,速度限制等)的前提下完成指定任务。
本文的目的是证明机器人部分穿刺过程的安全性。即,末端执行器从安全区域出发,并在任何操作时间内是安全的,且穿刺针到达靶目标位置时速度满足安全性限制。
如图2所示,R1、R2分别表示机械臂可以执行自由运动和减速运动的空间。Q1表示机械臂自由运动的终止平面,随后机械臂进入减速运动空间。Q2表示减速运动的终止平面,在穿刺针末端到达Q2平面时,穿刺针的速度与加速度均要满足相应的安全性约束,随后调整穿刺针的穿刺姿态准备穿刺。
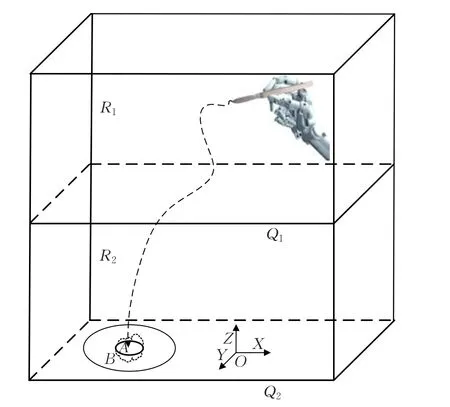
图2 穿刺运动空间模型
如果把穿刺过程的控制算法模型称为Ctrl,对于穿刺运动的整个控制过程,可以将其安全性质描述为:

公式(2)中,蕴含式前、后件中的safe表示安全区域,微分动态逻辑算子[Ctrl]表示控制过程。因此上述蕴含式表达了穿刺运动的末端执行器从安全区域safe出发,通过[Ctrl]的控制后运动过程中的所有状态依然保持在安全区域内。
假设机械臂的末端执行器用δ=(p,v,a)表示在当前位置δ.p时具有速度δ.v和加速度δ.a,显然有:

假设用五元组m=(pe,ve,vm,Max,Min)给出机械臂在运动过程中的某些约束概念。机械臂在运动过程中到达位于Q2平面上的终点m.pe(end point)时速度不大于m.ve,机械臂在运动过程中的速度不允许超过最大速度m.vm(max speed),m.Max与m.Min分别表示末端执行器的加速度在实际情况中的安全性限制,即-m.Min≤δ.a≤m.Max。
根据安全性描述,当穿刺针到达m.pe时,速度满足:

根据末端执行器在空间上的运动方式本文将其分解为在z轴方向上一维微分动态逻辑模型和在xoy平面上二维微分动态逻辑模型。
3 一维微分动态逻辑模型
末端执行器在z轴方向上的运动方式如图3所示。
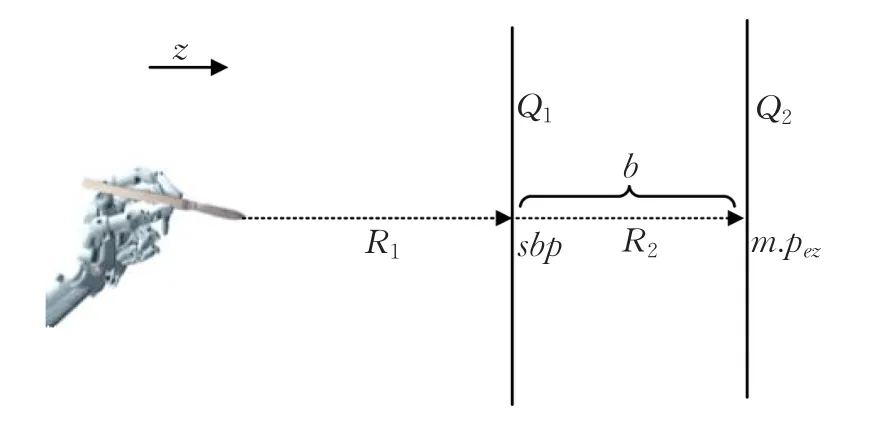
图3 Z轴方向上的运动学分析
图3 中,sbp为开始制动点(Start braking point),m.pez为末端执行器沿z轴运动的终点位置。空间R1和R2由边界Q1隔开。末端执行器沿z轴运动的位置不能超出边界Q2,即末端执行器的位置始终满足:

根据末端执行器在z轴方向上的运动方式建立微分动态逻辑子模型如下:
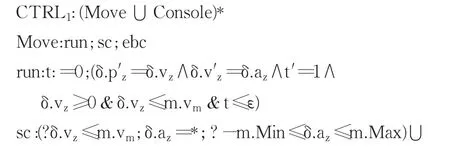

CTRL1表示末端执行器的运动控制由Move和Console两部分组成。Move由运动学微分方程run(kinematic differential equation)、速度控制 sc(speed control)和紧急制动控制 ebc(emergency braking control)三部分组成。δ.pz′给出了末端执行器的位置δ.pz的变化速率,即δ.vz,而δ.vz的变化率对应相应的加速度δ.az,当 0<δ.az≤m.Max 时末端执行器加速运动,当-m.Min<δ.az<0时末端执行器减速运动。
在实际情况中,由于在z轴方向上末端执行器的运动方向始终指向边界Q2,不存在相反方向的运动,所以用δ.vz≥0约束动力学微分方程。另外,末端执行器的速度不允许超过最大速度,即δ.vz≤m.vm。当该运动系统由离散跳转转到连续演化时,在连续演化开始之前将时间置零,即t:=0。因为该运动系统在实际中并非是理想的,所以会由硬件上的缺陷、通信的延迟等引入误差,导致连续演化并不能立即得到响应,因此假设在t≤ε(ε>0)内连续演化继续执行则认为控制策略生效。
速度控制sc由两个部分组成,符号⋃表示非确定性选择。若判断(符号?表示判断)末端执行器的速度δ.vz不大于最大速度m.vm为真,则加速度δ.az可以在[-m.Min,m.Max]中任意取值,即末端执行器自由运动;若判断δ.vz≥m.vm为真,则δ.az在[-m.Min,0]之间取值,使得末端执行器减速运动以保证运动速度不会超出控制。
紧急制动控制ebc的作用是在末端执行器的位置δ.pz超过制动点sbp或者控制台向末端执行器发出紧急制动指令command:=brake时以末端执行器允许达到的最大制动力开始制动。
控制台Console表示给出紧急制动指令command:=brake或者将末端执行器的约束值修改为任意值。例如:由于实际情况中靶点目标的移动从而将目标位置的取值m.pez修改为移动后的值。
3.1 归纳微分不变式
根据安全性要求,末端执行器在运动到终点位置m.pez时不会超过限制速度m.vez,用微分动态逻辑公式描述为:
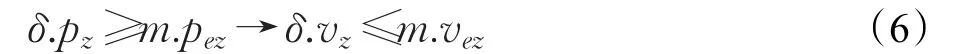
根据动力学系统要求,可以得到全局性的约束条件:
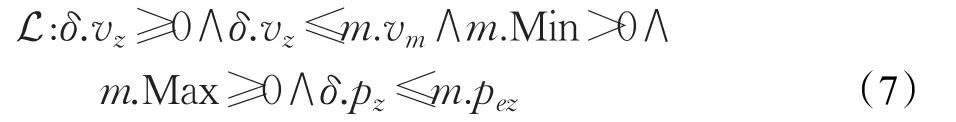
由于在z轴方向上,末端执行器到达终点位置m.pez(δ.pz≤m.pez)以前,其运动方向始终指向边界Q2,不存在反方向的运动过程,所以末端执行器的运动速度始终为非负值(δ.vz≥0)。末端执行器在z轴方向上的运动速度始终不会超过最大限速m.vm(δ.vz≤m.vm)。制动力m.Min>0确保末端执行器可以做减速运动,加速度m.Max≥0确保末端执行器可以做加速或匀速运动。
根据以上分析可以得到动力学系统可控性约束的微分动态逻辑方程,令:
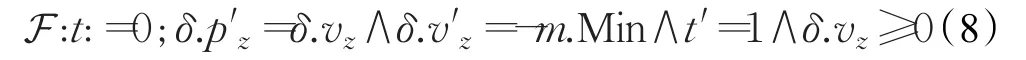
则
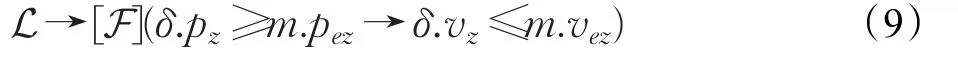
上述方程表示当末端执行器从满足全局性约束条件且没有通过终点m.pez的状态下出发,对于所有的连续演化过程,末端执行器以最大的制动力m.Min执行减速运动的状态都满足安全性约束δ.pz≥m.pez→δ.vz≤m.vez。
使用证明工具KeYmaera对上述公式推理证明得到,当初始状态满足δ.vz2-m.vez2≤2m.Min(m.pez-δ.pz)时,上述微分动态逻辑公式成立,即δ.vz2-m.vez2≤2m.Min(m.pez-δ.pz)表示在满足全局性约束条件下末端执行器以最大的制动力m.Min执行减速运动的状态都满足安全性约束,称该式为系统的一个微分不变式(differential invariant)。结合全局性约束条件可以得到系统的全局性初始约束条件Inv,该条件满足制动后的安全性约束,令:
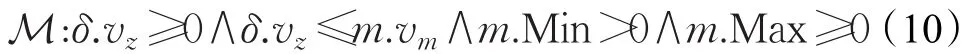
则
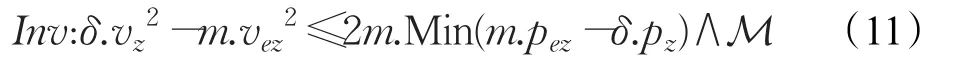
在实际操作情况中,需要考虑到特殊情况,例如末端执行器从一开始就以最大加速度加速运动,在到达制动点sbpz后开始减速运动并最终安全到达终点位置m.pez。用微分动态逻辑公式描述为:
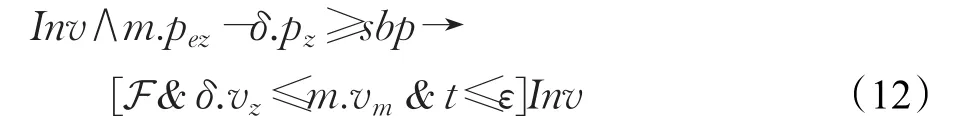
上述公式表示末端执行器从安全状态集出发并且以最大加速度δ.v′z=m.Max运行后仍在安全状态集中。又因为安全状态集Inv表示末端执行器无论以什么样的速度运动,之后以最大的制动力m.Min制动都可以满足终点位置的速度限制。使用证明工具KeYmaera对上述微分动态逻辑公式进行推理证明,得到:
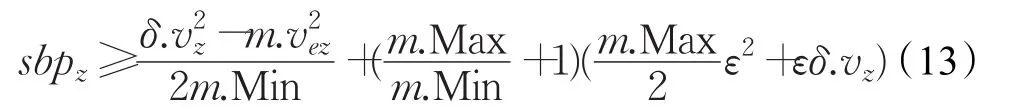
由上式得出了开始制动点sbpz位置的约束解。
3.2 参数可变的微分动态逻辑模型
由于在实际的医疗环境中存在诸多不可控因素,导致需要及时更改末端执行器的约束参数或靶点位置等信息,使得穿刺机器人仍然可以继续正确执行穿刺动作。例如:医生根据手术过程中的实际情况需要尽快完成穿刺动作而提高末端执行器的最大运动速度m.vm或最大加速度m.Max的取值;又或者,由于手术过程中靶点位置的移动需要及时更改靶点位置m.pe的取值等。对于上述情况控制台Console将及时更新m=(pe,ve,vm,Max,Min)的值为 m′。
由于不变式Inv是过程性约束,它更深层的含义是指当末端执行器目前的状态满足安全性约束则它之后的某个状态若满足不变式Inv的约束也必定满足安全性约束。因此,当目前的参数满足安全性约束,经Console更改后若仍然满足不变式Inv的约束,则更改后的参数也一定满足安全性约束,即
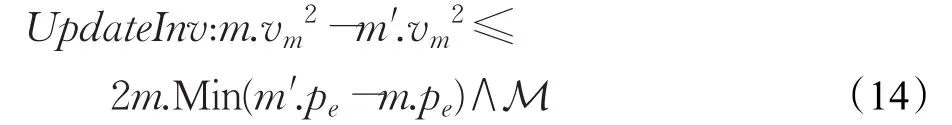
本文通过推理证明的方法分析说明在末端执行器的运动过程中更改约束参数的安全性,有以下微分动态逻辑公式:
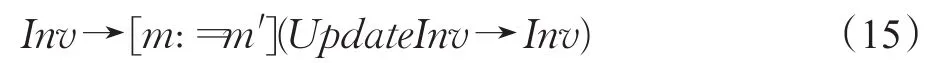
上述公式表示末端执行器从满足不变式Inv的状态下出发,对于所有的约束参数的更改[m:=m′],如果更改后的状态满足UpdateInv则所有的状态满足可控性约束。即
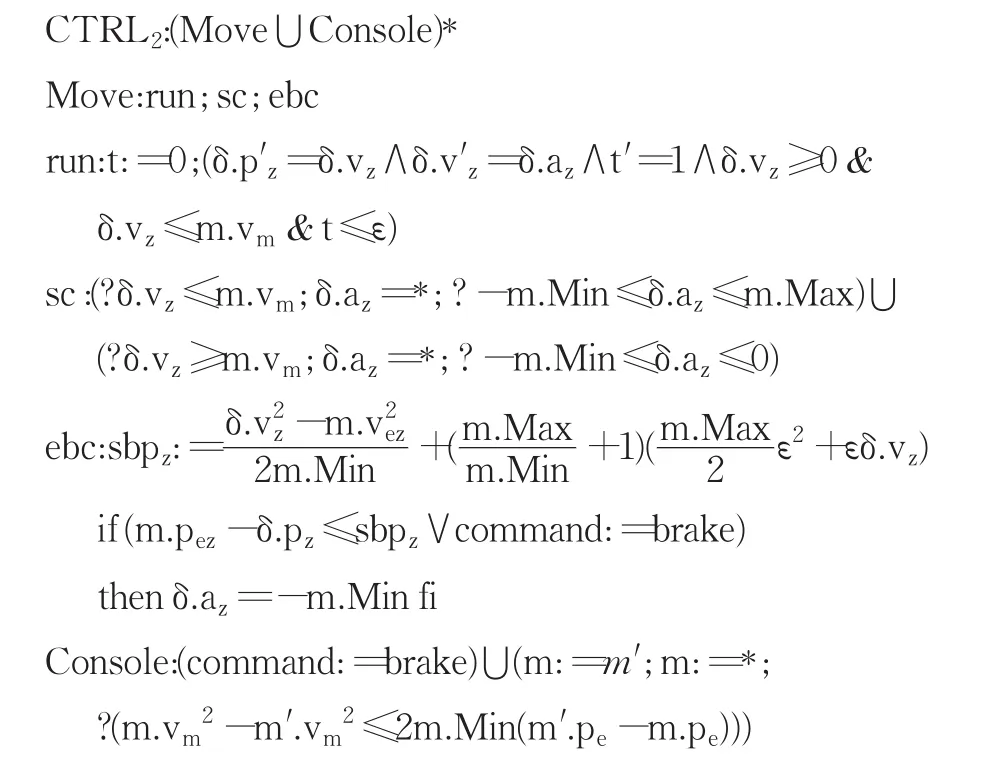
开始制动点sbp的取值是在最严格的条件下计算得到的,即在制动点前以最大的加速度m.Max加速运动,到达制动点以后以最大制动力m.Min做减速运动,且到达终点位置m.pez时满足最终的速度约束δ.vz≤m.vez。因此,当紧急制动控制ebc满足m.pez-δ.pz≤sbp时开始紧急制动,穿刺机器人的末端执行器在z轴方向上的运动一定满足安全性约束。
由于本文将末端执行器在空间上的运动方式分解为两部分,在以上一维空间运动控制模型的基础上,本文将进一步分析机器人在二维空间中的运动情况并建立二维微分动态逻辑模型。
4 二维微分动态逻辑模型
如图4所示,A和B为同心圆。区域A为执行穿刺的目标区域,区域B为末端执行器能够安全到达区域A的减速区域。区域A和B以外的区域为自由运动区域。A1和B1分别为A和B的边界;a、b分别为直线b1、b2与圆A的切点,且b1||b2。坐标系的原点O为末端执行器的启动位置。vx、vy表示末端执行器在x和y方向上的分速度。d和D分别为圆A和B的半径大小。
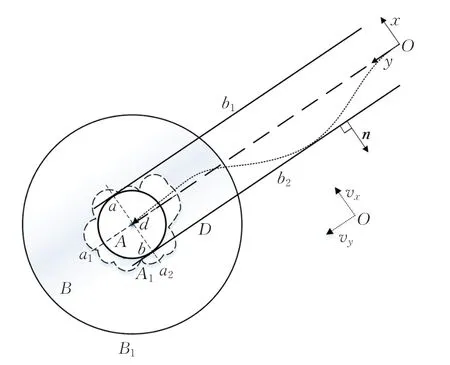
图4 xOy平面上的运动学分析
实际中,根据末端执行器的位置与靶点位置的关系可以分为以下两种情况:
(1)δ.pxy-Ao≥D,表示末端执行器处于可自由运动的区域。在该区域中,末端执行器可以以任意速度vx、vy运动,其中,0≤vx≤m.vm,0≤vy≤m.vm。当末端执行器到达边界B1时执行减速运动。
(2)d≤δ.pxy-Ao≤D,表示末端执行器处于边界A1与B1之间的减速区域之中。
经过圆心Ao(Ao即终点m.pe在xOy平面上的投影位置)的两条直线a1、a2为末端执行器终止运动的边界,即末端执行器在x和y方向上分别逼近a1、a2,但始终不会越过a1、a2。
由于末端执行器在xOy平面上的运动是自由的,分析可知spd=D,即假设Ao为最理想的靶点位置,D为满足约束性条件的最小的制动距离。在实际的医疗环境中医生不会允许穿刺针无终止地运动,为了保证执行动作的高效性,本文假设末端执行器必须在b1和b2之间的区域内运动,即牺牲运动的部分灵活性实现高效性。在这个区域内末端执行器可以在满足约束条件的情况下自由运动。
4.1 xOy平面上的运动学模型
根据末端执行器在xOy平面上的运动方式建立微分动态逻辑子模型如下:

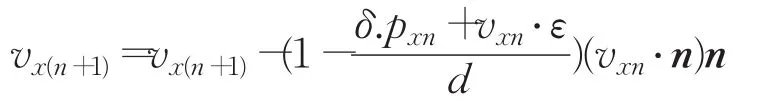
但由于在速度迭代似的反馈控制中存在延时,假设延时时间为ε。如图5所示,当传感器将末端执行器当前的位置pxn反馈给Console并由它更改末端执行器在x轴方向上的速度时,执行器的位置已到达δ.px(n+1)=δ.pxn+vxn⋅ε之后执行更改后的速度vx(n+1),此时可以保证末端执行器在速度迭代控制过程中存在延时ε的情况下依然不会超出约束边界。
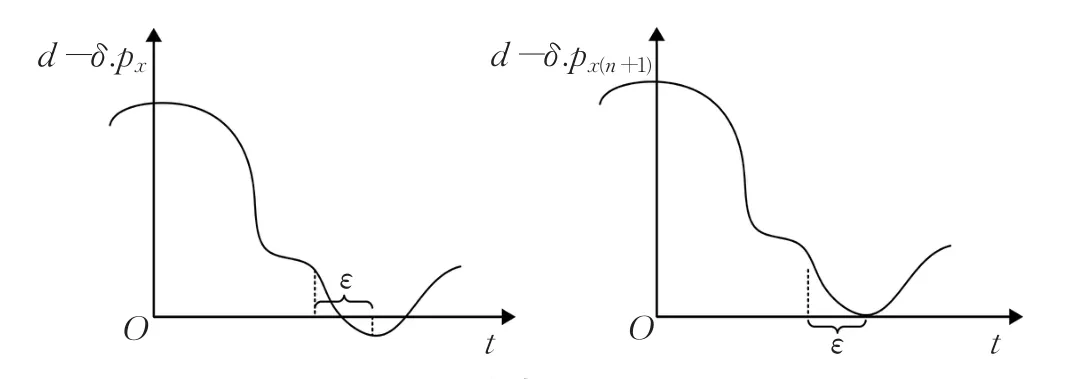
图5 迭代延时分析
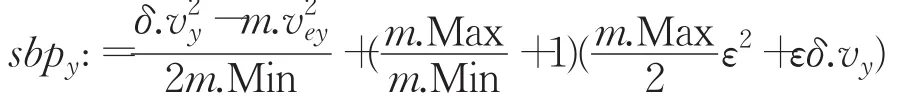
4.2 运动学问题的一般性验证模型
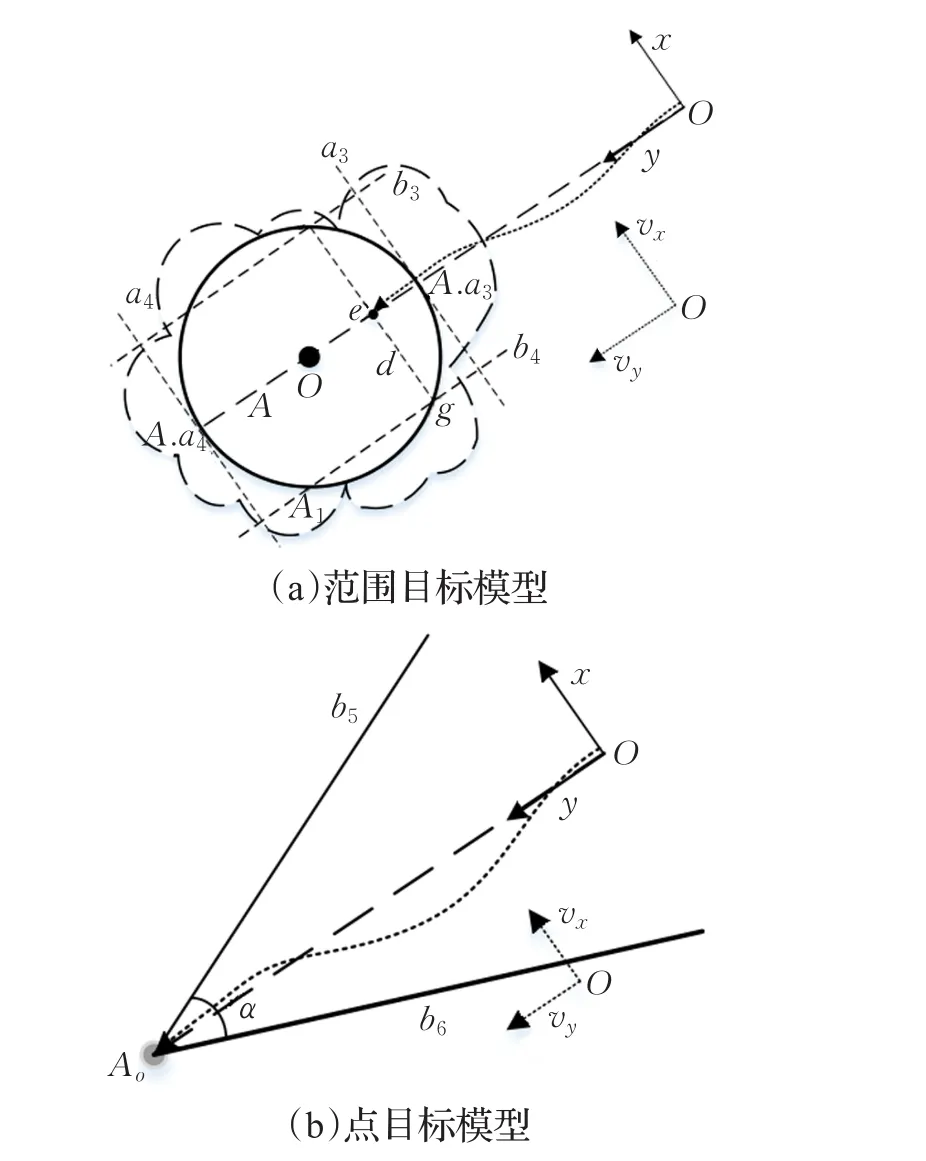
图6 安全运动的一般性形式化模型
因此当末端执行器在y轴方向上运动的终点位置由Ao变为近端终止点A.a3时,m.pey:=Ao-d。同理,终点位置变为远端终止点A.a4时,m.pey:=Ao+d,所以sbpy:=(Ao±d)-δ.py。因此,在 y轴方向上若要满足末端执行器最终停在圆A内y轴方向上的任意位置时,开始制动点的取值范围为:
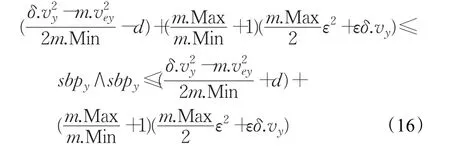
假设末端执行器停止在圆A内e点处,则在x轴方向上的约束边界由b1、b2变为b3、b4。开始制动点到边界b3、b4的垂直距离为为末端执行器在y轴上的停止位置。因此:
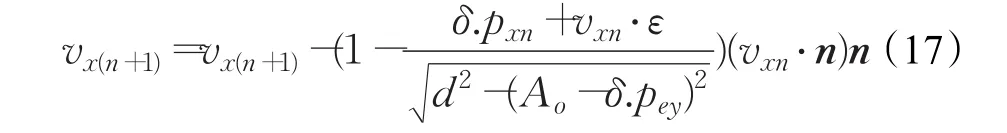
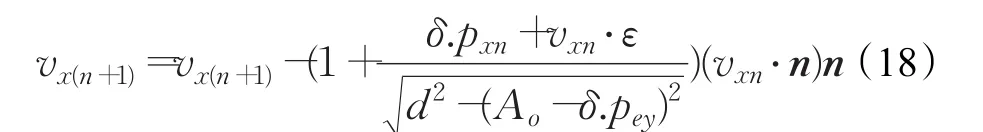
综上所述,得到末端执行器在xOy轴方向上的运动方式建立微分动态逻辑子模型如下:

从运动学角度分析,以上微分动态逻辑模型对于机器人到达某一指定区域的安全性问题具有普适性约束,可以作为空间运动学安全性问题的一般性验证模型。若末端执行器要求准确到达某一点,则可牺牲部分灵活性,保证运动的安全性。如图6(b)所示,可以以靶点为顶点做锥形空间,则末端执行器在x轴方向上约束条件为:
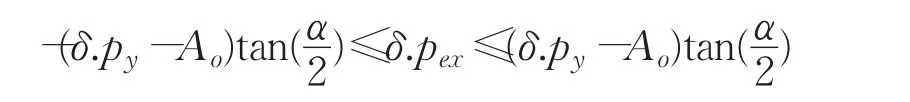
为了证明用微分动态逻辑描述的混成系统的安全性,本文结合机器人控制系统的安全性描述,将以上微分动态逻辑模型Ctrl4写入后缀名为key的文件后,导入KeYmaera中进行自动推理证明。在KeYmaera自动证明的过程中,为了加快验证进度,人为地加入了一些验证过程中必要的逻辑法则。最终KeYmaera弹出“property proved”,证明了模型的安全性。
5 结束语
本文通过微分动态逻辑的方法对穿刺机器人自主系统部分安全性问题进行了验证。从运动描述中提取出形式化模型,通过推理规则精化出满足系统安全性要求的微分不变式及系统约束参数可变的安全性证明。此外,本文从穿刺机器人的实例出发提出了一种可以证明空间运动学安全性问题的一般性形式化模型,该模型能够适用于与本文工作相似的空间运动学设计问题。
