面向点云模型的交互式位姿调整系统

关日钊，陈新度，吴 磊

广东工业大学 机电工程学院，广州 510006

1 引言

STL文件格式最早是由美国3D System公司推出，是三维实体模型系统的一个接口标准，其接口格式规范，目前已被工业界认为是快速成型领域的标准描述文件格式，广泛应用于制造业、地理信息系统、医学影像等领域[1-2]。其采用以点云数据为基础，组成一系列无序三角面来表达三维实体模型的表面，在快速成型制造系统中已经成为了一种标准的数据输入，可以通过三维建模软件或三维扫描仪生成[3]。

目前，STL模型的位姿调整工作主要利用Solid-Works、UG等建模软件，通过建模时确定模型的建模坐标系和输出STL模型格式时改变模型的输出坐标系这两种方式来完成。由于建模软件不能直接操作只有点云数据的STL格式文件以及在修改模型建模坐标系上缺乏灵活性，本文开发出一套面向点云模型的交互式位姿调整系统，其直接的操作对象为STL模型文件，与普通的调整方式相比，其在操作上更加方便和灵活。

2 系统设计

系统软件由Qt与OpenGL作为开发平台，其中Qt是一个跨平台应用程序和UI开发框架。使用Qt只需一次性开发应用程序，无需重新编写源代码，便可跨不同桌面和嵌入式操作系统部署这些应用程序。而OpenGL是专业的图形程序接口，功能强大的底层图形库，因其硬件无关性、建模方便性、出色编程性等优点，在仿真领域有着广泛应用[4-5]。

在本系统中OpenGL只处理与3D图形的绘制，基本上不提供创建用户界面的功能，所以为OpenGL应用程序创建用户界面必须使用其他的图形工其包。而Qt的OpenGL模块很好地解决了这个问题，它提供了一个继承自QWidget的OpenGL部件类QGLWidget，使得该部件类能够像Qt其他部件那样使用，还可以在绘制窗口部件时直接使用OpenGL的API接口。在Qt中为OpenGL提供支持的类主要有以下几个：

（1）QGLWidget：用来渲染OpenGL场景的Qt部件。

（2）QGLContext：用来封装用于OpenGL场景渲染的部件。

（3）initializeGL（）：注册函数，在此设置GL的渲染绘制属性、定义显示列表、载入固定纹理等初始化工作。initializeGL（）在调用paintGL（）之前只被调用一次，之后不再调用。

（4）paintGL（）：绘制函数，在此使用OpenGL中的接口进行场景绘制，QGLWidget的paintEvent（）将会自动调用paintGL（）进行部件的显示绘制。

2.1 系统功能模块设计

系统框架主要分为6个模块，分别为GL模块、UI模块、IO模块、图元模块、变换模块和约束模块。如图1所示。

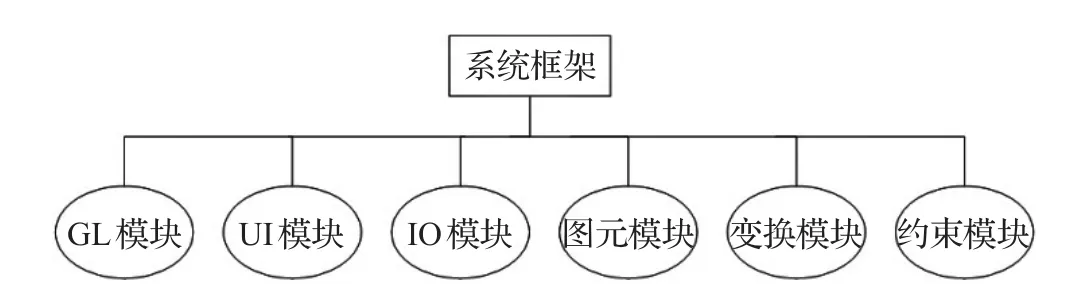
图1 系统框架图

其中GL模块负责管理OpenGL各种场景和模型渲染等操作；UI模块主要负责窗口、菜单等UI界面元素的管理以及鼠标工具的管理；IO模块负责STL模型文件的输入与输出管理；图元模块主要负责基本图元的构建和管理；变换模块负责模型位姿的变换；约束模块负责检测模型变换是否引起冲突。

2.2 系统流程设计

系统基本操作流程如图2所示。

下面将对关键的步骤进行简单的描述，具体的实现过程和原理将在第3章论述。

（1）“打开STL文件”操作包含模型载入和显示两个过程。在模型载入的过程中，由于STL存在较多的冗余点，因此在载入的过程中需要对冗余点进行滤除。在显示的过程中，主要利用了OpenGL中的显示列表对模型进行渲染。

（2）“构建图元”操作是利用鼠标通过选择点云来构建直线和平面两种基本图元。其中包含了图元拾取和图元构建这个两个方面的内容。

（3）“选择配合方式”操作是利用直线和平面这两种基本图元进行轴配合或平面配合。系统提供5种配合关系选择，分别是轴平行配合、轴重合配合、平面平行配合、平面重合配合和原点配合。

3 关键技术研究

3.1 STL冗余点滤除

STL文件的最大特点是由一系列以顶点为基础的三角形面片以无序排列方式组合在一起，每条边只能被两个三角面片共用，而且每一个小三角形面片必须与相邻的三角形面片共用两个顶点，每个顶点通常被重用6次左右，造成了巨大的数据冗余。一般情况下，冗余顶点数约为面片数的5/6倍[6-7]。

冗余点的滤除主要在载入文件时进行，若省略这个过程，会给后面构建图元操作带来不便。目前对于冗余点滤除的方法主要有平衡二叉树法[8]、三轴分块排序法[9]、哈希表法[10-11]等。卫炜[12]等人实验表明，在三角片数量在5万以上时，哈希表法在上述三种方法中效率最高的，因此本文选择哈希表法进行冗余点滤除。

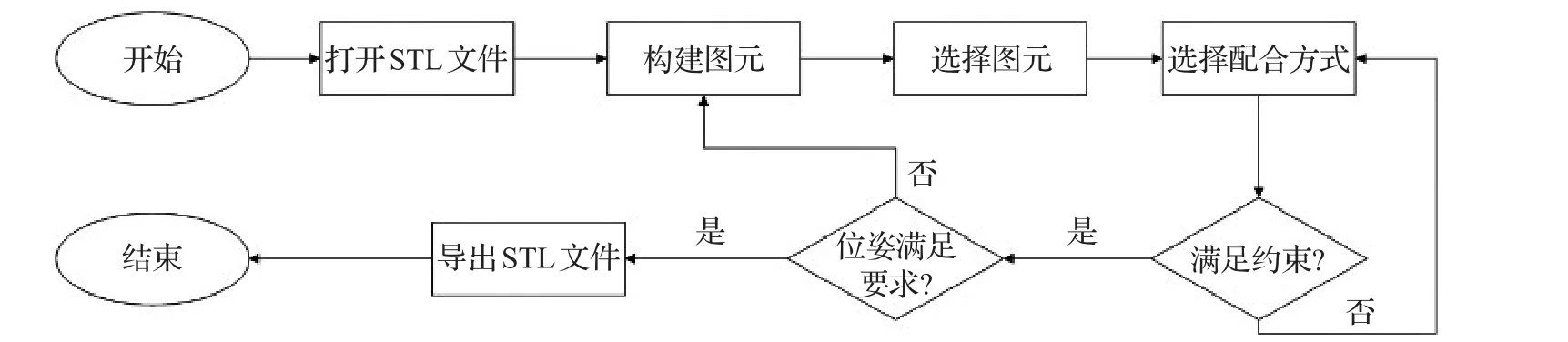
图2 系统操作流程图

哈希表是将一组关键字映射到一个有限的连续的地址集上，并以关键字在地址集中的“像”作为记录在表中的存储位置的一种表。本算法中使用链地址法处理冲突的哈希表[13]，如图3所示，Array是一个链表数组，每一个元素代表链表的头指针，其大小是随STL顶点数变化而变化的。Node是链表中的节点存储结构，如图4所示，每一个节点包含了一个点的X、Y、Z坐标和一个指向下一个节点的指针。

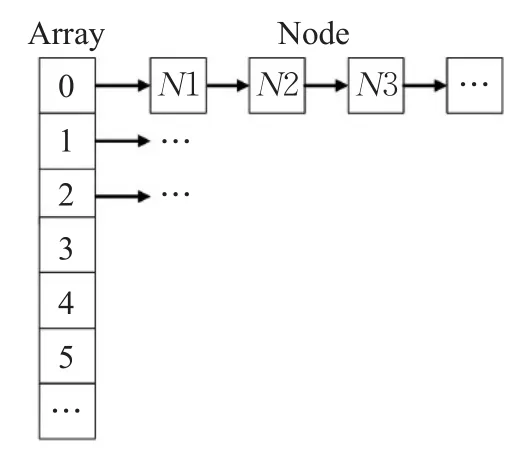
图3 哈希表结构图

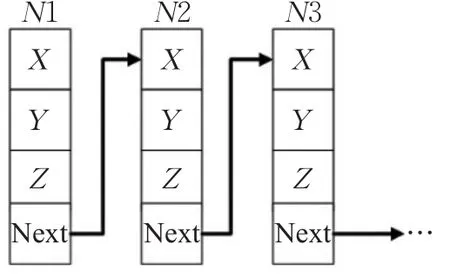
图4 节点结构图

哈希函数的“好坏”直接影响出现出图的频繁程度，也即直接影响哈希表的查询效率。STL冗余节点滤除的依据是顶点坐标，即哈希表的关键字为顶点坐标(X,Y,Z)。本算法根据关键字可以计算出哈希表键值，取值为：

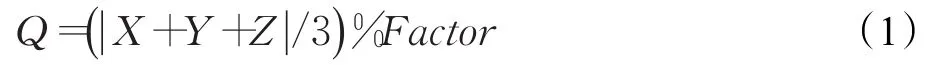
其中

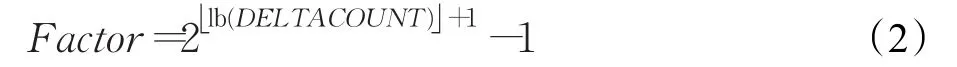
由上述可知，Q代表记录在哈希表的位置，通过每一个顶点坐标计算出来的键值可以马上定位到该点所属的链表，然后在所属链表中通过与每个节点数据进行比较去筛选出相同或者相近的点出来，本文是通过筛选相近的点来进一步减少冗余点数量。表1为算法针对4个不同的STL三维模型筛选后的结果。

表1 哈希表冗余点滤除算法结果

3.2 图元拾取

图元拾取过程是利用鼠标拾取OpenGL渲染环境下的各种图元，是图元构建和图元配合两个步骤的实现基础。

3.2.1图元拾取原理

OpenGL为了解决拾取问题，提供了一种基于名字堆栈和命终记录的选择机制。在OpenGL中，拾取物体是利用拾取矩阵和投影变换，将拾取的范围限制在鼠标热点的有效区中，一旦触发鼠标事件就进入选择模式并将有效区初始化，最后利用拾取矩阵拾取有效区内的物体。有效区的定义由glPickMatrix（）函数来完成。一旦拾取成功，就以记录的形式返回与拾取物体相关的信息，并生成一个记录表示一个物体被命中。

3.2.2 图元拾取步骤

（1）调用void glSelectBuffer（）函数指定用于返回点击记录的数组，其中size决定了拾取一次最多可以返回多少个被选取对象。

（2）调用 Glint glRenderMode（）函数并传入 GL_SELECT作为参数进入选择模式。

（3）使用void glInitNames（）和glPushName（）对名字栈进行初始化，其中name是一个无符号整型参数，代表了每一个物体的ID，选取操作就是利用这个ID来获取被选中的物体对象。

（4）定义用于选择的视景体并且通过gluPickMatrix（）函数构造出一个挑选矩阵，并协同投影矩阵，把绘图限制在视口的一个小区域内，一般是靠近光标的位置。在确立了选择模式并使用了特殊的挑选矩阵之后，在靠近光标位置处绘制物体就会导致选择点击[5]。

（5）交替调用绘制图元的函数和操纵名字栈的函数，为每一个相关的图元分配一个适当的名称。

（6）退出选择模式，并处理返回的选择数据。

3.3 图元构建

图元的构建需要通过STL模型的点云数据进行构建，如图5所示。图中浅蓝色的点云为工业机器人底座的STL模型数据。本系统提供直线图元和平面图元构建功能。

图5 底座模型点云渲染图

3.3.1 直线图元构建

直线图元的构建需要通过选择两个顶点来进行构建，如图6所示。红色直线是利用鼠标在点云中选择两个点构建出来的。

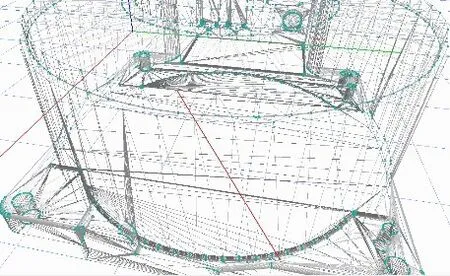
图6 直线图元构建图

3.3.2 圆形平面图元构建

圆形平面图元的构建是根据“三点一面”原理。如图7所示。图中红色平面是利用鼠标在点云中选择三个点构建出来的。

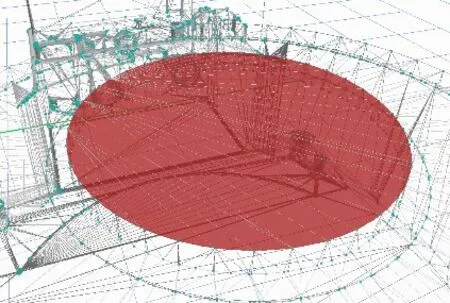
图7 平面图元构建图

3.3.3 对称平面图元构建

对称面的构建必须构造两个面，并且两个面之间的夹角不为0°或180°，如图8所示。

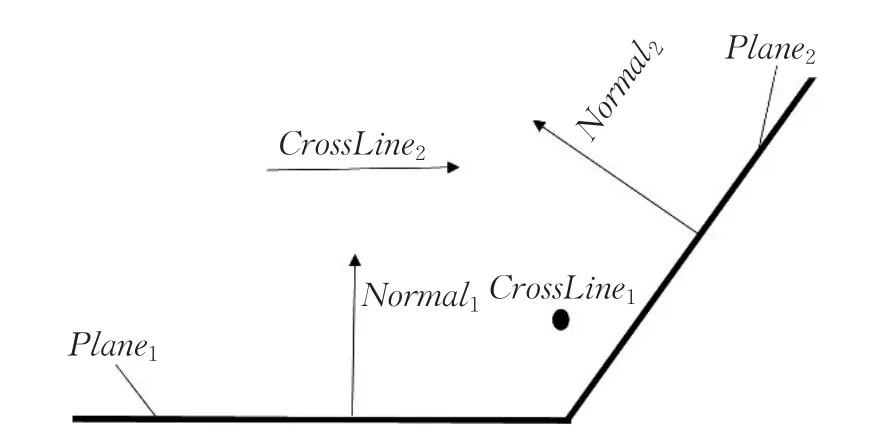
图8 对称面构造示意图

构建步骤主要为：

（1）将Normal2和Normal1进行叉乘得：

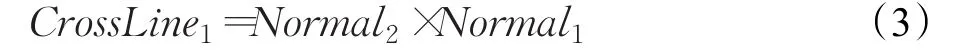
（2）将Normal1和CrossLine1进行叉乘得：

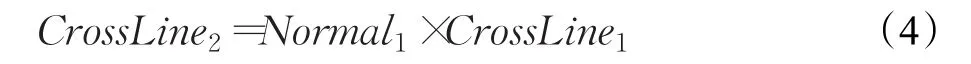
（3）将模型上所有的点同时投影到CrossLine2上，投影过程中通过比较获得在CrossLine2上投影距离最长的两个点P1和P2。

（4）过P1点沿Normal1的方向上确定一个点P3，过P1、P2、P3三点作一圆面，该圆面便是模型的对称面，如图9所示，红色平面为对称面。

图9 对称平面图元构建图

3.4 图元配合

3.4.1 配合关系

整个配合过程是利用新构建的直线或者平面图元对已知的坐标系进行轴配合、平面配合或点配合，此坐标系是一个自定义的右手坐标系，可以当作新的建模坐标系，如图10所示，红线、绿线和蓝线分别代表X轴、Y轴和Z轴。图中模型为机器人底座的STL模型渲染图。

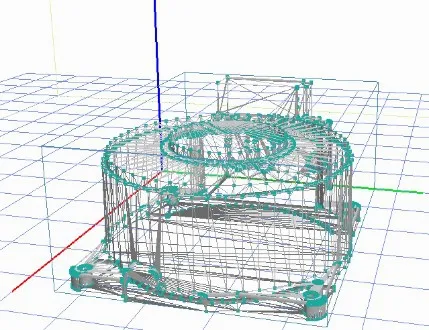
图10 建模坐标系与STL模型图

轴配合中的“轴”指的此坐标系的X轴、Y轴和Z轴，平面配合中的“平面”指的是此坐标系X-Y平面、Y-Z平面和Z-X平面，点配合中的“点”指的是此坐标系的原点。

（1）当选择直线图元进行轴配合的时候，可分为两种情况，一种是轴平行配合，如图11所示。另一种是轴重合配合，如图12所示。图中黑线为选中的直线图元，与X轴进行轴配合。

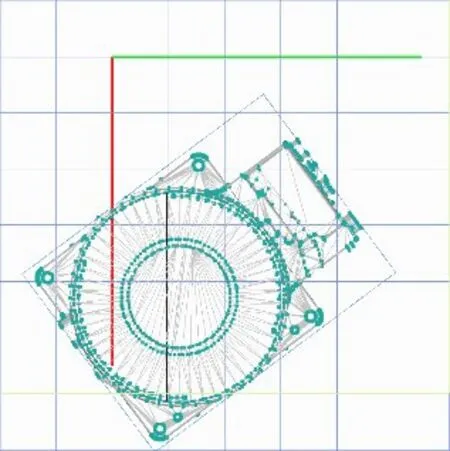
图11 轴平行配合

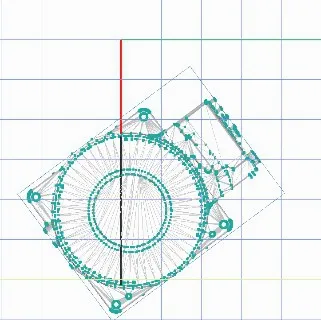
图12 轴重合配合

（2）当选择平面图元进行面配合的时候，也可以分为两种情况，一种是面平行配合，如图13所示。另外一种是面重合配合，如图14所示。图中黑线为选中平面图元的法线，平面图元与平面Z-X进行面配合。

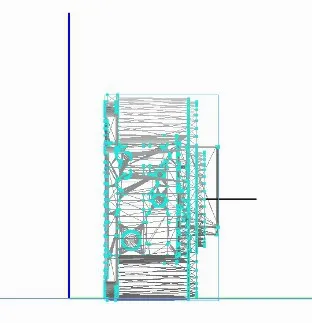
图13 面平行配合

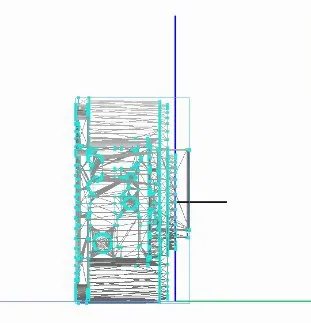
图14 面重合配合

当选择原点配合的时候，此时配合的图元可以是直线图元的首点或者平面图元的圆心。图15为直线原点配合，图中黑线为所选直线图元。图16为面原点配合，图中黑色透明平面为所选平面图元。

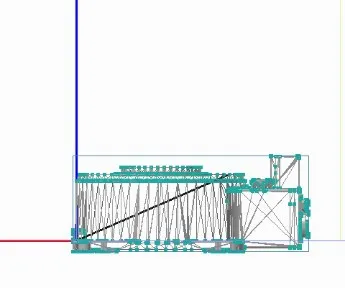
图15 直线原点配合

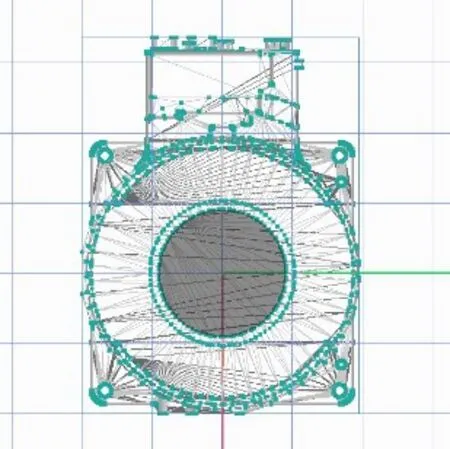
图16 平面原点配合

3.4.2配合原理

整个配合的结果是通过进行直线或平面配合而得出一个旋转平移矩阵，然后利用这个矩阵对模型进行相对于新的建模坐标系的一次位姿变换，从而实现了改变模型建模坐标系位姿的效果。

上面提到在配合过程中需要计算一个旋转平移矩阵。其中旋转矩阵是一个可以绕任意轴的旋转矩阵，计算此矩阵需要用到旋转四元数法。四元数是一种高级的数学工具，被应用于各种工程领域，如导航、机器人和计算机图形学[14]，它是一种高阶复数，可以表示为式（5）[15]：

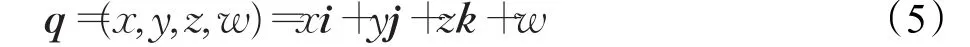
其中，i,j,k满足式（6）和式（7）：

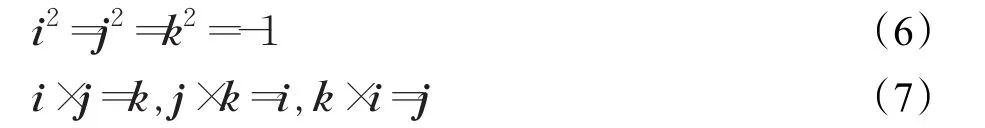
由于i,j,k的性质和笛卡尔坐标系三个轴叉乘的性质很像，所以可以将四元数写成一个向量和一个实数组合的形式，如式（8）所示：

假设向量V绕任意轴N(nx,ny,nz)旋转α角度得到向量V1，定义此变换过程的四元数表示为Q(x,y,z)，那么 Q(x,y,z)可以表示为式（9）[16]：

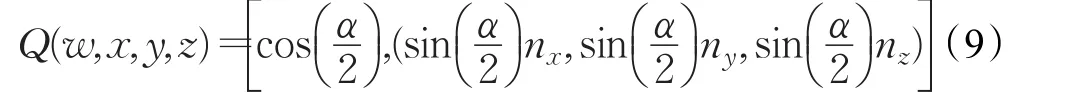
在实际OpenGL编程中要实现模型的旋转操作需要利用到旋转矩阵去实现，所以就需要把四元数公式转化成矩阵形式来表示，如式（10）所示：

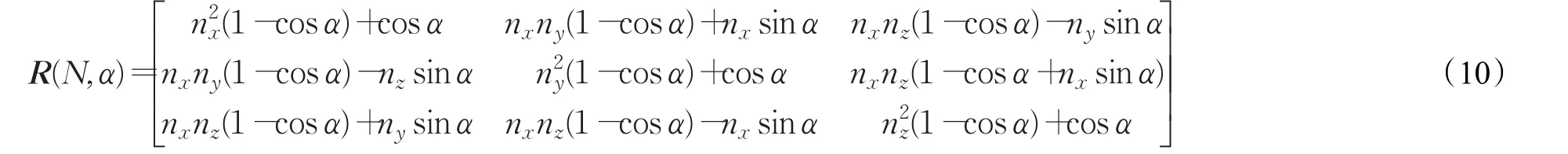
其中nx,ny,nz为任意旋转轴，α为旋转角度。

结合式（9）和式（10）可推导出式（11）为：

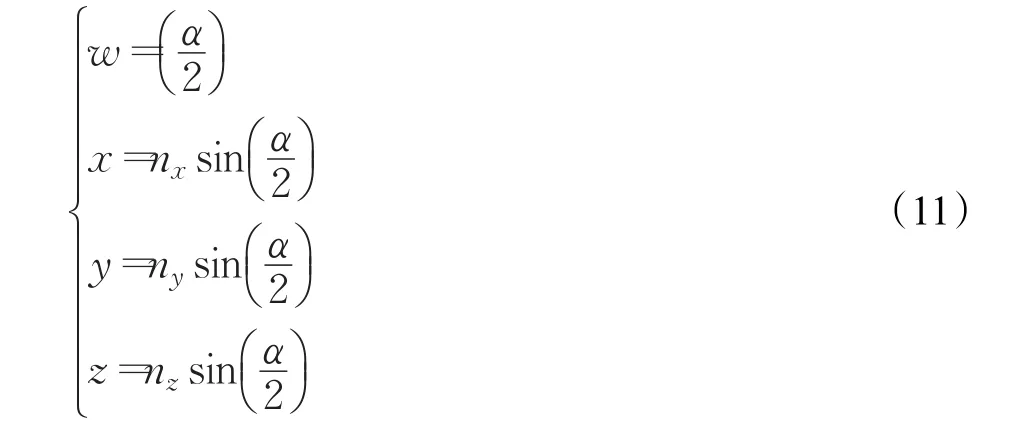
把式（11）代进旋转矩阵可以得出四元数的矩阵表现形式，如式（12）所示：

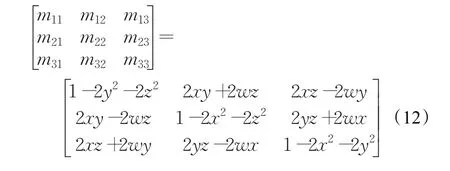
当对直线进行X轴平行配合时，假设所选择的直线图元由a和b两点组成，可以表示成一个向量Vab，设向量Vx=(1,0,0)，则根据式（13）计算出Vab与Vx之间的夹角θ1：

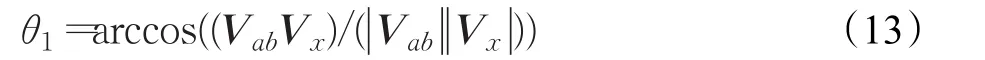
在求出夹角后，对Vab与Vx进行叉乘得到旋转轴Vr。最后把θ1和Vr代入式（12）便可求出旋转矩阵。

当对平面进行X-Y面平行配合时，求出所选择平面的法向量Vn，已知X-Y面的法向量为Vxoy=(0,0,1)，利用Vn和Vxoy两个向量则可以根据上述直线配合中求夹角和旋转轴的方法算出最后的旋转矩阵。

4 系统验证

4.1 非扫描型STL模型调姿

非扫描型STL模型指的是利用三维建模软件建模导出的STL文件。图17为一个待调姿机器人底座的STL模型。

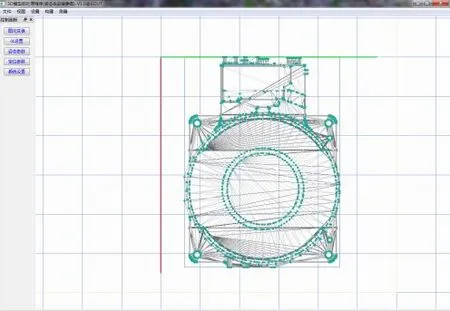
图17 待调姿机器人底座模型

通过构建底座平面作为变换对象，再进行“原点配合”变换操作来完成调姿工作。图18为最终的调整效果。

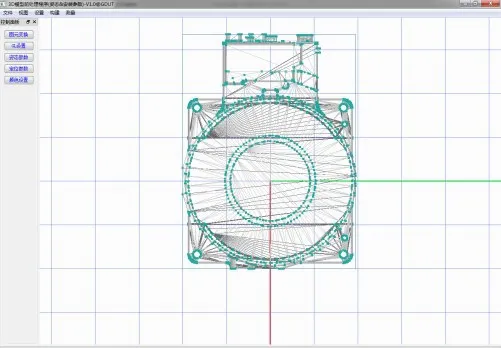
图18 调姿后机器人底座模型

4.2 扫描型STL模型调姿

扫描型STL模型指的是利用三维扫描仪扫描导出的STL文件，图19为一个待调姿的马桶STL模型。

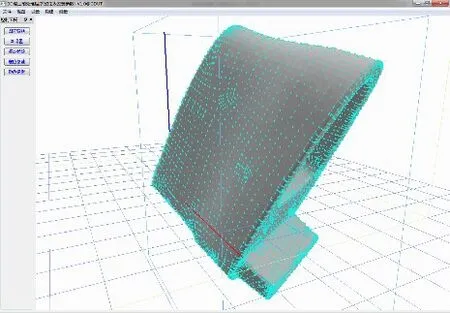
图19 待调姿马桶模型

由于马桶模型不是通过一般的软件来建模，而是通过三维扫描仪进行三维重建建模的，所以通过简单的构建平面去进行调整是比较困难的，因此需要通过构建模型的对称面作为变换对象，当对称面与Z-X平面重合便达到所需要的效果，如图20所示。

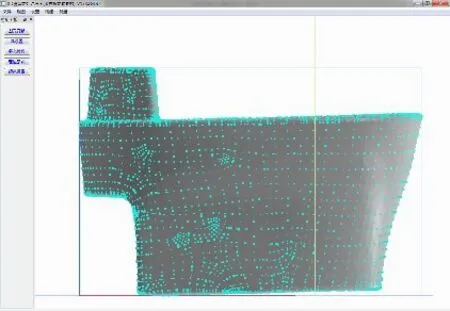
图20 调姿后马桶模型

5 结束语

本文结合Qt+OpenGL平台开发出一套面向STL点云模型的交互式位姿调整系统可以改变STL模型建模坐标系的位置姿态。通过交互式的手段构建出辅助图元，利用这些辅助图元来实现模型建模坐标系的位姿调整。适用于通过建模软件导出的STL模型和通过三维扫描仪生成的STL模型。此外，在机器人离线编程领域中经常需要用到STL模型建立仿真环境，无可避免需要对导入的STL模型进行位置姿态调整。因此，本系统在离线编程软件的开发中具有辅助性的作用。