Hellmann-广义Morse势Schrödinger方程的散射态解

陈文利，樊亚云, 殷娟娟

(西安培华学院智能科学与信息工程学院，陕西 西安 710125)

基于在散射态的研究中肯定了原子核的存在，系统的散射态解析解及相对应的本征值包含着有效的量子信息，散射理论的研究越来越引起大家的注意，然而除了氢原子和核谐振子之外大部分量子体系都不能解析求解。为了求解散射态解析解及散射相移，近似表达非线性离心项是求解不同量子系统的可行手段，逐步形成了指数形式[1-2]、Pekeris形式[3-4]等近似办法，利用这些近似办法将径向薛定谔方程化简为可解的微分方程。为了获得更广泛的应用，我们注意到两个或更多势的组合给不同的应用提供了一个重要的结果[5-6]。例如，Onate等求解了包括了由Hallmann 势场、Yukawa势场、库仑势场组成的组合势场的薛定谔方程[7]。由Rosen-Morse、Pöschl-Teller 和 Scarf 势组合而成的广义反双曲势场的薛定谔方程的束缚态被解析求解[8]。最近我们注意到Hellmann-广义Morse势，其表达式为[9]

(1)

其中：De为离解能；re平衡键长度；a,b为势长；α势屏参数。当取定不同参数时，势场可退化为Hellmann势场、广义 Morse势场、Yukawa 势。然而，由于其薛定谔方程中非线性中心项的存在，散射态的解析求解一直没有被涉及。本文利用恰当的近似办法处理离心项，推导其薛定谔方程的散射态解析解，得到相对应的散射态相移公式，数值求解特征值方程并和MATHEMATICA程序包所得数据进行对比，最后讨论了简化为屏蔽库仑势的特例。

1 散射态的近似解析解

球坐标体系下薛定谔方程的表达式为

(2)

E为系统的能量本征值， 取势函数为Hellmann-广义Morse势， 设波函数Ψnlm(r,θ,φ)=r-1unl(r)·Ylm(θ,φ)，并代入方程(2)得径向方程为

(3)

由于离心项l(l+1)/r2的存在，方程(3)不能被解析求解，和我们先前处理离心项的办法一样[10-13]，本文利用近似公式

(4)

为了说明近似公式的有效性，取公式(4)中参数α不同时的近似公式曲线图(见图1)，不难发现，当参数α越小时，近似效果越好，取α=0.01时势包处近似曲线几乎重合于1/r2曲线，同时，绘制量子数n=1时径向概率密度，势包处束缚离子的几率也是取到峰值。

图1 势函数、径向概率密度、近似表达式关于r曲线

把近似公式(4)代入方程(3)中，径向方程(3)可化简为

(5)

引进无量纲变量

z=1-e-αr，

(6)

定义c=(eαre-1),方程(5)化简为

(7)

考虑边界条件z→1(r→∞)，设径向波函数的表达式为

(8)

其中，参数

(9)

将方程(8)代入方程(7)，化简得

(10)

观察微分方程(10)的结构，其解恰为超几何函数的表达形成

(11)

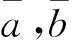
(12)

结合方程(8)和方程(11)，Hellmann-广义Morse势薛定谔方程的波函数解析表达式为

(13)

其中，N为归一化常数。

为了研究散射态的解析性质，方程(12)中的参数满足关系

(14)

借助超几何函数变换公式[14]

(15)

(16)

同时，利用

(17)

把方程(17)代入方程(16)中,波函数的渐进行为可表示为

(18)

与散射态边界条件u(r)→2sin(kr-(1/2)lπ+δl)(r→∞)[15]比较可知，相移δl和归一化常数N可解析表示为：

(19)

(20)

进一步讨论散射振幅及其解析性，散射振幅可表示为[16]

(21)

(22)

结合方程(9)、(14)，解析求解方程(22)，特征值满足的方程为

(23)

本文所推导出的特征值方程(23)和文献[9]中所获得束缚态能级公式(16)本质是相同的。

2 讨论

当De=0时,势函数化简为屏蔽库仑势

(24)

相对应的特征值方程(23)化简为

(25)

对于得到的束缚态能级方程(25)，可以对a和b进行赋值，让屏蔽参数α作为能量方程的自变量，对束缚态能级-E进行讨论(见图2)，随着量子数增加，会导致粒子变得弱有界甚至是变成无界的，粒子在这些边界是很容易被释放的。

为了进一步验证推导的正确性, 取参数a=0,b=-1，势函数简化为一般屏蔽库仑势[17-18]，特征值方程(23)化简为

(26)

数值求解特征值方程并和文献[17]计算的结果进行对比，从数值表2可以得到，本文求解得到的特征值数值解较先前数据更加接近MATHEMATICA程序包所得数据。

3 数值结果

取势参数De=5，r=1.6,a=1,b=1，数值求解特征值方程(23)，并与MATHEMATICA程序包所得数据进行对比，数值结果(见表1)验证了当势参数α越来越小，近似效果越好，和图1中的分析是一致的。表2为退化为屏蔽库仑势本征值方程(26)数值解，本文所得数据较先期所得数据更好地逼近真实值。

表1 特征值数值解

表2 屏蔽库仑势特征值数值解

4 结论

对含有Hellmann-广义Morse势薛定谔方程，利用恰当的近似公式近似表示离心项，求解了任意l波薛定谔方程散射态解析解，得到了复杂的相移公式及按超几何函数表示的径向波函数，利用波函数的渐近行为解析求解了能级方程。 数值计算了特征值的数值结果并和MATHEMATICA计算所得特征值进行比较，验证本文所求解的特征值更好地逼近真实值，同时讨论了势参数De=0的特例，并和我们先前计算一般屏蔽库仑势所得数据进行比较。