涡流发生器对不同弦长风力机翼型气动性能的影响

2018-09-18龚玉祥周晓亮程明哲

西华大学学报（自然科学版） 2018年5期

龚玉祥，周晓亮，程明哲

(浙江运达风电股份有限公司，风力发电系统国家重点实验室，浙江杭州 310012)

风力机叶片的大型化趋势使得叶片长度越来越长，为了保证叶片根部的强度，叶片的结构设计上大多选用大厚度的翼型，这就导致了在大攻角下，大厚度的翼型更加容易发生气动分离现象，导致叶片吸收风能的能力降低，从而降低了风轮效率[1]；因此，控制流动分离和减小叶片阻力成为风力机气动研究领域的热门问题之一。

1947年，美国联合飞机公司的Bmynes和Taylor首次提出了将涡流发生器(VGs)应用于推迟飞机机翼的边界层分离[2]。VGs 安装在叶片上表面边界层内，并与当地来流保持一定的侧向夹角。VGs产生的尾涡扰动分离区内的气流，使边界层上部高能气流与近壁低能气流混合，增加近壁流体的动量和能量，延缓分离，同时VGs 技术安装工艺简单，经济性高；因此，被应用于大型风力机上[3-4]。Lin通过风洞试验和数值模拟，得到了涡流发生器安装位置应该离分离点较近的结论[5]。Johansen等在数值计算中将涡流发生器两侧的边界层条件设为对称边界及周期性边界，研究了VGs 对风力机叶片气动性能的影响规律[6]。张磊等采用CFD方法分析了VGs对风力机专用翼型DU 91-W2-250气动性能的影响规律，对比了14°攻角下光滑翼型和VGs 翼型的流动特性，揭示了VGs对翼型的流动控制机制[7]。赵振宙等考虑了转捩效应的影响，采用SST全湍流模型和Gamma-Theta转捩模型对翼型DU 91-W2-250进行了数值模拟，研究结果表明转捩模型计算结果较试验值更加吻合[8-9]。

在翼型上安装涡流发生器的研究中使用的翼型弦长大都为0.6 m，而实际风力机叶片的厚翼型截面对应的弦长可达4 m[10]；因此，本文在不改变涡流发生器尺寸和安装位置的情况下，研究了弦长变化对翼型气动特性的影响规律。

1 计算模型

1.1 几何模型和网格划分

翼型选用DU系列风力机专用翼型DU97-W2-300为研究对象，此翼型试验模型弦长为0.6 m，装有VGs的试验数据由荷兰Delft大学通过风洞实验得到[11]，可验证数值计算方法的可靠性，模型如图1所示。

图1 几何模型

计算段翼型的展向长度与试验模型保持一致，长度为0.175 m，计算弦长分别为0.6 、1和1.5 m，在翼型弦长20%处共安装5组VGs，具体几何尺寸如图2所示。VGs的形状为三角形，其弦向有效长度为17 mm，高度5 mm，攻角为16.4°，每组内的两个三角形叶尖距离为10 mm，相邻的两组VGs的排列周期为35 mm。

采用ANSYS ICEM划分结构化网格，对VGs处进行网格加密处理，第1层网格高度为0.01 mm，网格增长率为1.1，保证y+≤1.5，网格如图3所示。

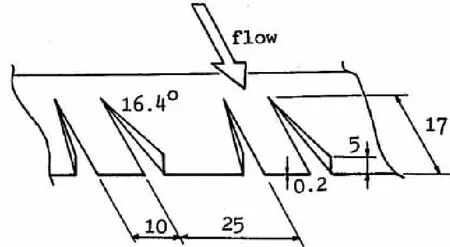
图2 涡流发生器尺寸参数

图3 网格划分

1.2 数值模拟方法

3种不同弦长的翼型计算雷诺数相同，计算雷诺数为Re=2.0×106，攻角范围为0°到20°，所采用的数值计算方法与文献[8]相同，即使用转捩模型进行数值模拟计算，定义三维翼型两侧的断面为周期性边界条件。

2 计算结果分析

2.1 模型验证

图4为转捩模型计算的升力系数曲线与试验数据的对比图。从试验数据可以看出，VGs使翼型失速现象明显延迟，从无VGs翼型的临界攻角12.37°延迟到有VGs 翼型的16.51°，将最大升力系数由1.55提升到了1.97。从计算结果可以看出，转捩模型计算结果与试验结果吻合良好。在攻角范围为0°≤α≤18°时，转捩模型计算误差仅为5.28%，在α>18°时转捩模型计算误差仅为6.51%。由此可见，转捩模型对于涡流发生器的数值计算精度高，其模拟结果能真实地反映VGs翼型的气动特性。

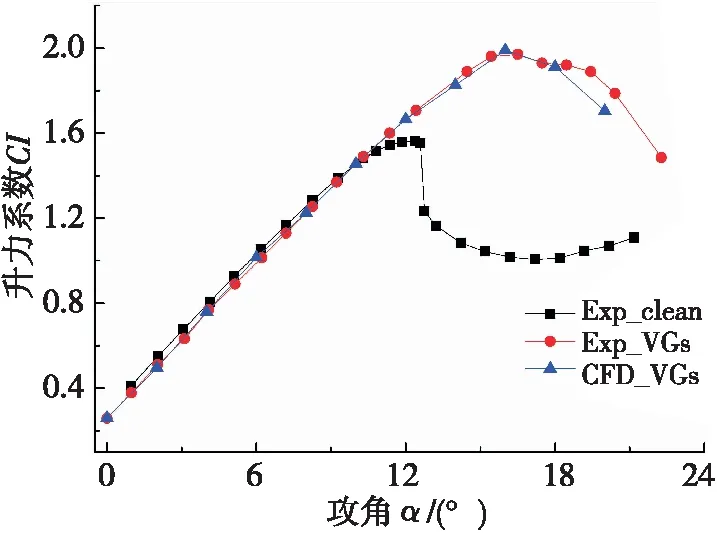
图4 升力系数曲线

2.2 VGs对流场和表面压力分布的影响

从升力系数的变化趋势可以看出，α=18°位于VGs翼型的升力系数曲线的临界攻角附近，此时翼型表面可能会出现气流分离现象，截取如图5所示的位置1和位置2对应的截面，截面1为每组VGs的中心线，截面2为相邻2组VGs的中心线。

图5 位置1和位置2

图6为截面1和截面2的流线图。从两个截面的流线图可以发现两个截面的流场是不同的，截面1尾缘处未出现明显分离区域，截面2尾缘处出现明显的分离区域，这表明翼型段上VGs的下游气流在沿展向分布上是不均匀的。

图7为截面1和截面2与翼型交线的压力分布图。可以看出两个截面的压力分布只在安装VGs附近是不同的，交线1上压力分布出现负压峰值，而交线2上出现负压谷值。流线图和压力分布揭示了流动产生涡流的根本原因，对于单个涡流发生器而言，当气流经过时，其两侧变成了压力面和吸力面，造成两侧压力的不平衡，形成高能量的涡流，注入到近壁低能量气流后，增加了近壁流体的动量和能量，从而抑制边界层的分离，推迟翼型失速。

图6 攻角为18°下不同截面的流线图

图7 攻角为18°下不同截面压力分布图

2.3 翼型弦长变化对流场的影响

图8为安装相同VGs，翼型不同弦长的升力系数变化规律图。可以看出，安装了相同的涡流发生器，3种不同弦长翼型的升力系数较光滑翼型均得到了提升，对翼型弦长为0.6 m的升力系数的提升最为有效。在攻角范围为0°≤α≤14°时，3种不同弦长翼型的升阻力系数变化趋势基本相同，在α>14°时，相同攻角下，随着翼型弦长增大，翼型升力系数减小。当攻角为16°时，弦长1 m的翼型升力系数较0.6 m时减小了4.35%，弦长1.5 m的翼型升力系数较0.6 m时减小了10.82%。

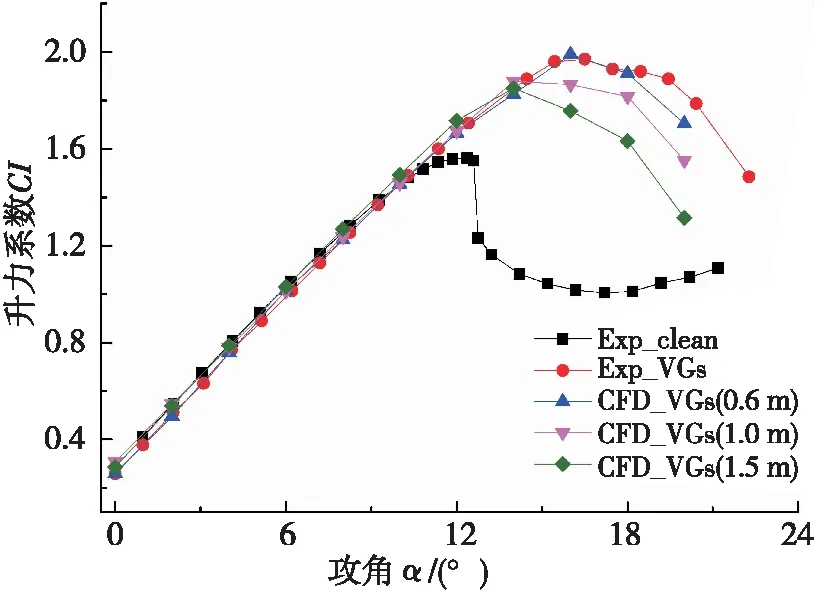
图8 弦长对升力系数的影响

基于以上分析，截取得到3种弦长下攻角分别为14°、16°和18°时截面2的流线图，如图9所示。可以看出：当攻角为14°时，3种弦长的翼型尾缘处均未有明显的分离区域；当攻角为16°和18°时，随着翼型弦长的增大，翼型尾缘的分离区域均逐渐变大。这是因为在雷诺数相同的情况下，翼型弦长的增大意味着来流速度的减小，当流体沿着翼型表面流动并掠过VGs时，形成的涡流的动量和能量减小，与近壁低能流体混合后的流体能量将会减小，同时混合后的流体所经过的距离增大，这就导致了翼型尾缘分离区域的增大。基于此，预测当翼型的弦长增大到4 m时，安装本文中的涡流发生器于弦长20%处，其性能将进一步降低甚至可能失去推迟翼型失速的作用；因此，在设计适合于风场中运行的风力机叶片的涡流发生器时，应当考虑叶片截面的实际弦长。