挠性航天器智能模糊控制算法

2018-09-18，，，，

中国空间科学技术 2018年4期

，，，，

中国运载火箭技术研究院研究发展中心，北京100076

为了解决挠性航天器模型不确定性和外部干扰带来的问题，现阶段国内外一般采用鲁棒性和抗干扰能力强的滑模变结构控制器实现航天器姿态机动控制[1-3]。但是滑模变结构控制器中的符号函数会带来控制力矩高频抖振问题[4-6]。智能模糊控制算法能够根据接近滑模面的程度来确定参数的变化方向，从而确保控制力矩的平滑变化，有效消除控制力矩的高频抖振。

现阶段国内外一般使用滑模变结构姿态控制器实现对航天器的姿态机动控制[7-8]。对于非线性系统，滑模变结构姿态控制器通常采用等效控制方法保证滑动模态在滑模面上运动，从而实现对航天器姿态机动控制。但是等效控制主要针对确定系统，并假设控制是在理想情况下进行。在实际工作中，由于航天器结构不会处于特定的稳定状态条件下，同时再受到外界干扰等因素的影响[9]，航天器控制系统的状态变量到达滑模面后，不能在滑模面上保持稳定的滑动运动，而是在滑模面上下进行来回穿越滑模面的运动[10]，进而引起控制系统发生极限环振荡的干扰现象[11]，这种现象称为抖振现象。抖振现象会引起控制系统的高频振荡，进而对系统造成伤害。

本文针对挠性航天器滑模变结构姿态控制器控制力矩引起的高频抖振问题，设计一种挠性航天器智能模糊控制算法，对航天器自身的控制参数进行模糊化智能处理，在保证控制器鲁棒性和抗干扰能力的同时消除控制力矩的高频抖振。算法首先将模糊控制与滑模控制结合，对姿态控制器的参数进行自适应模糊处理，根据切换面的变化将趋近律的系数进行模糊化处理，重新解算模糊数据；然后应用连续饱和函数代替符号函数设计姿态控制器；最后通过算法达到滑模面的程度调整边界厚度层，使算法结果能够最终到达滑模面。仿真计算结果满足工程应用要求。

1 算法设计

智能模糊控制是一种非线性智能控制算法[12-15]。智能模糊控制是主要结合专家的知识和思维，进行学习与推理、联想和决策的过程[16-18]，适用于非线性、时变及纯滞后系统的控制。

本文提出了对挠性航天器进行智能控制的智能模糊控制算法。该算法首先将基于指数趋近律的滑模控制算法和模糊控制算法结合使用，使用切换函数和其导数作为模糊控制器输入，根据模糊规则实时将趋近律的系数进行模糊化处理，从而便于调整趋近律参数。然后使用连续饱和函数替代符号函数设计准滑模变结构控制器，通过模糊控制算法调整控制整个滑模面的边界层厚度，确保滑动模态变量能够在控制系统作用下平稳到达滑模面。算法在提高对航天器大角度姿态机动控制能力的同时，可以有效抑制控制力矩的高频抖振现象。

1.1 趋近律设计

挠性航天器的滑模变结构控制器使用指数趋近律设计。由于指数趋近律中有符号函数存在，会引起控制力矩的高频抖振，有可能造成执行机构的损坏，同时挠性附件也会由于姿态角速度的变化而引起振动，导致航天器姿态失稳。智能模糊控制算法在趋近律中引入切换函数，并通过其导数的变化规律对趋近律参数进行智能处理。利用模糊控制器来模糊化处理滑模变结构控制的趋近律参数，对变结构控制算法进行实时控制。

设计的智能模糊控制算法趋近律要求控制系统加快系统到达滑动模态的速度，同时还要抑制在控制信号中存在的高频抖振问题，算法首先在滑模变结构控制时引入切换函数，利用切换函数的正负值变化来实时修正航天器进行姿态控制时使用的指数趋近律。当切换函数和指数趋近律无法通过确切函数关系进行表述时，需要根据获得的切换函数实际计算值，通过智能模糊控制算法对指数趋近律系数进行修正，消除高频抖振，实现控制力矩的平滑过渡。

挠性航天器智能模糊控制算法使用二维模糊控制，其基本原理如图1所示，输入量为清晰变量e和de/dt，输出精确的控制变量u。

在图1中，知识库中的变量μ、R和fd都是通过离线计算独立得到。其中变量μ表示隶属函数，其作用是在模糊化转换计算中将数字量转换为对应的模糊量的函数进行归类并存储。R表示控制规则库，主要集中管理能够实现近似推理计算的算法和F条件语句。fd表示清晰化方法库，主要归纳存储能够将模糊量实现清晰化计算处理的算法。参数ke和kec是模糊控制算法具有比例缩放功能的量化因子模块。航天器控制系统的输入、输出清晰值信息可以通过这两个量化因子模块进行相应比例的缩放。同时量化因子模块还承担着连接模糊控制输入和输出接口并将其与相邻模块匹配的功能，在匹配模糊控制过程中对模糊控制器某些性能也进行相应改善。D/F表示的是模糊化模块，主要功能是实现将清晰量进行计算并转化为模糊量；A*R是模糊推理运算模块，经过A*R模块计算得出模糊量U；F/D表示的清晰化模块将模糊量转化成清晰量，这3个模块构成模糊逻辑控制器的核心。在模糊推理过程中，为了使数值更容易辨析，需要将量化因子模块设置到模糊化模块前匹配模糊控制过程，并将比例因子模块设置到清晰化模块后得到精确计算的数据信息。

为了将变量进行适当放大和缩小，以便与相邻的模块更好匹配，同时便于对清晰值进行比例变换，智能模糊控制算法中，重新设计量化因子和比例因子，并进行相应的匹配。

(1)量化因子设计

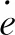
由于外部环境的多变性，物理论域X和模糊论域N在多数情况下不同，相同情况仅停留在理论情况上。因此量化因子起到一个变换系数的作用，从物理论域中将清晰值映射到模糊论域中。量化因子的变换作用在模糊控制算法中的实质是将输入的实时信号获取范围进行相应的放大或者缩小，从而适应特定的模糊论域映射要求。设已知输入变量x1的一个分量xj的物理论域：

(1)

xj的模糊论域：

(2)

量化因子：

(3)

当输入变量所在的物理论域X发生变化时，将设置好的量化因子进行及时更改，使新的输入量发生变化后还能映射到原有的模糊论域中。量化因子的具体用法如下：用量化因子将输入变量的分量变换为模糊算子时，由于模糊论域Nj的限制，为了保证无论输入变量是否在正常范围内，都能使变换出的n∈Nj，限制如下：

(4)

如果模糊论域N的值为离散值，取nj为3～7之间的某个正整数，设模糊论域的计算如下：

Nj= [-nj-nj+1 … -1 0 1

…nj-1nj]，nj>0

(5)

若由n=kjx算出的n恰为正整数，则取模糊论域中的值；如果算出的n不是正整数，按靠近原则取成整数，具体计算如下：

(6)

式中：sgn为符号函数；int为取整函数。

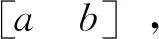
(7)

(2)比例因子设计

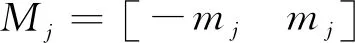
(8)

如果某时刻得到的模糊控制算法出量为n1∈M，则经过比例变换之后得到的控制量：

u1=n1ku∈U

(9)

量化因子和比例因子是智能模糊控制算法与外界连接起来的接口，其功能是对实际测量得到的信号进行比例变化控制，而实际测量信号的有效控制会直接影响采样信号对航天器系统的调节。在实际工程的控制中，仅仅增大量化因子会使控制系统上升速率变快，可能导致超调量过大，调节时间过长，情况严重时甚至会发生强振荡，无法稳定控制系统。仅增大比例因子会使系统的调节时间变小，增强系统的稳定性。因此可以根据挠性航天器的表现调节量化因子和比例因子的大小使其趋于稳定控制。

设挠性航天器的滑模变结构控制律函数：

u=K1sgn(s)+D1s+ω×(Jω)-

(10)

式中：ω为航天器本体在惯性空间中的角速度；J为航天器在本体坐标系下的转动惯量，航天器为耦合组合体，由刚性本体和挠性附件组成；Jmb为航天器在本体坐标系下的转动惯量；q为航天器在惯性空间下的姿态角四元数；q0为航天器在惯性空间下的姿态角单位四元数；s为滑模控制面；K1和D1为趋近律系数；k1为比例因子。

指数趋近律函数：

(11)

式中：r为控制面半径系数；ε为增益参数。

当s>0时式(11)变为：

(12)

求解式(12)，得到：

(13)

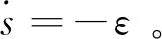
由于K1=Jmbε，D1=Jmbr，Jmb>0。所以在控制过程中，随着s趋近于0，需要减小K1的同时再减小D1。但是无法建立s与K1、D1的确切函数关系。智能模糊控制算法根据确切的数学模型实现这一步的智能控制策略，趋近律模糊推理原理如图2所示。

模糊规则进行推理运算，从而得到对应的模糊量s″，然后引入反模糊化模块，同时使用重心法解算，从而完成模糊量向清晰量的运算。

Ku1和Ku2分别是输出K1和D1的比例因子，是由模糊论域到物理论域的变换系数，从而得到实时的K1和D1值。

1.2 修正饱和函数边界层厚度

式(10)设计的控制律切换函数工作时会对控制力矩产生干扰，进而引起高频抖振，干扰严重时甚至会使挠性附件产生谐振，进而快速发散，对航天器结构安全产生极大的安全隐患。为防止这种抖振对结构产生破坏性影响，控制算法采用连续饱和函数代替符号函数，设计挠性航天器准滑模变结构控制，引入的饱和函数：

(14)

式中：k为滑模控制面的边界层厚度，滑动模态的到达时间可以通过对控制面边界层的厚度调节进行有效控制。

采用饱和函数改进的指数趋近律：

(15)

指数趋近律引入饱和函数进行设计，由于饱和函数中控制面的边界层厚度固定，设其厚度值为k。因此无论k取值如何趋近零，控制系统的滑动模态都无法完全到达滑模面。航天器通过滑模变结构进行有效控制时必须依赖切换函数数值对2个清晰输入量的系数进行实时修正，这样才能确保控制系统的滑动模态到达指定的滑模面。由于切换函数和指数趋近律之间的关系无法用显性函数表示，此时需要引入模糊控制算法，通过智能推理模糊算法，引入实时计算的切换函数值修正指数趋近律的系数。因此指数趋近律的微分方程：

s(t)=

(16)

从式(16)可知，在靠近滑模面的过程中，对切换函数动态过渡影响最大的参数是r。控制系统的滑动模态向滑模面接近的速度随着r的增加而变快；同时主要的干扰——挠性模态振动幅值也会随之变大。控制系统的滑动模态到达边界层后，参数ε和r的值越大，说明模态越接近滑模面。但是控制系统无法精确解算出参数ε和r的具体数值，因此也就无法建立这2个参数与滑模面s的确切函数关系。

为解决上述问题，需要引入自适应模糊逻辑算法控制参数ε和r，不依靠显性函数关系，而是根据实际计算进行模糊推理，输入s及其导数，同时输出变量变为ε和r，通过这一模糊推理计算实现智能控制。

2 仿真验证

为验证算法有效性，以挠性航天器滑模变结构控制的物理参数为输入条件，引入智能模糊控制算法进行仿真验证。仿真过程中的航天器模型以携带太阳翼板的卫星为研究对象，考虑轨道摄动的连续变化影响，航天器动力学模型：

(17)

式中：X为航天器状态矢量；F(X,t)为动力学模型主要摄动项；ΔR(t)为动力学模型次要摄动项拟合函数；w(t)为随机误差。

在挠性航天器本体坐标系OXYZ下，原点O在航天器质心上，X轴方向航天器头部方向为正，Y轴为航天器纵向对称面内垂直于X轴方向，指向航天器上方为正，根据右手定则确定Z轴。航天器的其他相关参数如表1所示。

挠性航天器主体的惯量矩阵：

(18)

挠性附件与航天器主体的耦合矩阵：

δ=

(19)

根据工程应用背景，航天器工作时受到的干扰力矩：

(20)

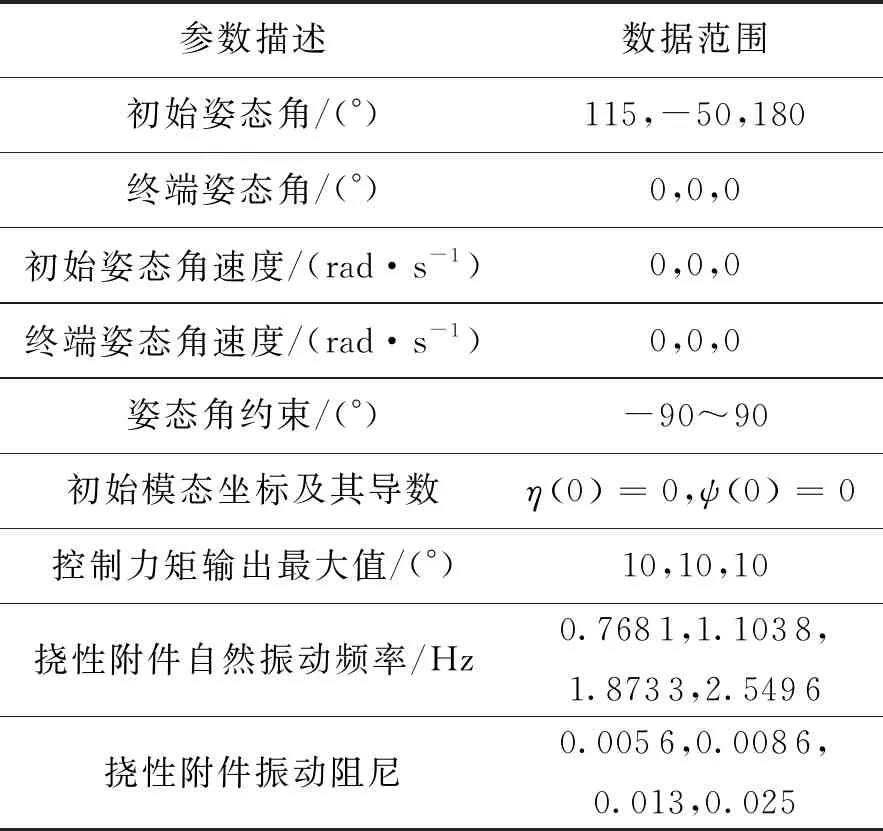
表1 挠性航天器参数表

本文提出的智能模糊控制算法将基于指数趋近律的传统滑模控制律参数进行模糊化处理，使用连续饱和函数替换符号函数，应用模糊逻辑对传统滑模控制进行自适应智能处理。从图4～图6的仿真结果可以看出，在挠性航天器大角度姿态机动控制中引入智能模糊控制算法，使航天器姿态角的稳定控制能力得到提高，有效抑制了由控制力矩引起的高频抖振问题，并且航天器稳定控制的收敛速度加快，使得该算法更具实际应用价值。