多机理下的卫星寿命预测方法与应用

，，

北京空间飞行器总体设计部，北京 100094

卫星是由专用有效载荷、姿态与轨道控制、结构与机构、热控、电源和测控等多个分系统组成的复杂系统，绝大多数卫星具有一次发射、长期使用的特点。卫星在轨服务过程中，其剩余寿命直接影响到卫星规定寿命要求满足的程度和寿命末期的处置策略，尤其对于卫星星座而言，卫星剩余寿命直接影响星座维持与补网计划，关系到星座可用性和连续稳定运行的能力。因此，预测卫星寿命并尽可能提高结果的可信度在工程中具有重要意义。

当前，有关卫星产品的寿命预测研究主要集中在部组件层次，一般是针对具有退化或渐变规律的产品，例如蓄电池、推力器、驱动机构等，提出某一产品的寿命预测方法[1-9]。而由于卫星系统的复杂性，整星的寿命预测研究非常少，现有方法主要是通过估算剩余推进剂来预测卫星剩余寿命[10-13]，这类方法没有考虑卫星突发故障和退化失效的情况，其应用有固有的局限性。

根据国内外卫星在轨故障统计[14-16]，卫星寿命终结不仅和燃料耗尽有关，也和随机失效、退化失效有关。因此，准确的寿命预测应完整考虑突发故障、退化和消耗多种因素，并反映这些因素尤其是突发故障导致的在轨寿命分布的动态变化。本文针对卫星寿命预测的现实需求和以往方法的不足，针对随机失效提出了随单星工作时间和系统结构变化的剩余寿命预测模型，并综合随机失效、退化、消耗及其在轨变化规律，给出了多机理下的整星寿命预测方法。这一方法既可用于单星剩余寿命预测，也可用于星座备份星替换策略的制定。

1 卫星寿命与失效的特征

1.1 星上产品的寿命特征及卫星到寿原因分析

按照失效机理不同，星上产品的寿命特征一般可分为以下3类：

1)随机寿命类，即产品寿命服从随机失效分布，可能很快发生在轨故障并永久失效，也可能长期正常运行并远远超过设计寿命。星上多数产品可归为这一类，例如通用电子产品。

2)退化寿命类，即产品特性服从特定的退化规律并在可预见的时间范围内必然达到寿命，例如蓄电池、太阳电池阵、行波管等。

3)消耗寿命类，一般是指推进剂等消耗性物质，当消耗到规定阈值时，产品到寿。

此外，某些产品的寿命可能具有多种特征，例如行波管放大器既有退化失效也有随机失效，铷钟既有消耗寿命也有随机失效等。这类产品在处理时需要分析多种机理。

根据星上产品的寿命特征和国内外卫星故障情况[14-16]，卫星长期在轨工作过程中，寿命终结的原因一般包括：

1)由于突发故障导致整星失效。这类故障的发生具有随机性，故障产品在失效前的长期工作中没有明显的性能变化，往往在某种诱因下突然失效。例如2003年2月，泰国通信卫星-3在发射5年10个月后，由于电源系统短路造成整星失效；2000年3月，ERS-1卫星发生姿态控制故障导致任务失败,服役结束。在没有其他类型故障和消耗性物质足够的前提下，卫星实际运行时间可能远超出其设计寿命。

2)由于消耗性物质用尽导致卫星到寿。例如星上剩余推进剂达到规定值，卫星不得不进行离轨操作或直接退役。这种情况下卫星并未发生故障，通常已经超过规定的工作寿命要求。

3)由于产品性能退化到不可接受的程度导致卫星到寿。典型情况例如太阳电池阵效率下降导致整星功率不足、行波管增益下降导致射频通道失效等。

1.2 卫星随机失效分布的特点

由于退化寿命和消耗寿命具有相对确定性，有关产品的设计寿命一般留有足够余量，因此在卫星系统可靠性分析中，通常仅分析随机失效。

卫星系统可靠度一般根据设备或分系统可靠性预计值利用系统可靠性模型计算得到。由于卫星大量采用冗余设计，典型的系统可靠性曲线如图1所示，这一曲线可以拟合为威布尔分布。

由于指数分布具有“无记忆性”，即产品的工作寿命和产品已工作多长时间无关，这在处理很多工程问题时具有极大的方便性。因此，也可假设卫星服从指数分布，此时卫星的失效率：

(1)

式中：λs为卫星失效率；Ts为卫星的规定寿命，R(Ts)为根据卫星系统可靠性模型计算得到的规定寿命的可靠度。卫星指数分布如图1所示。

由图1可见，在规定寿命期内，卫星采用指数分布是偏保守的。从国内外经验看，卫星随机失效通常取威布尔分布，并在很多情况下为了处理的方便，假设服从指数分布[17-18]。

2 随机、退化和消耗寿命的分析方法

2.1 基于随机失效的卫星剩余寿命

尽管星上设备种类很多，但如前文所述，根据系统可靠性模型最终可以近似得到一个整星随机寿命分布。利用这一分布，通过蒙特卡罗仿真可以得到基于随机失效的卫星剩余寿命。但这一过程中有两个关键问题：

1)卫星在轨时间是持续增加的，但仿真产生的随机失效时间可能小于卫星在轨时间。因此，需要剔除卫星已工作时间的影响。

2)随机失效产品可能在任意时刻发生故障。常见的情况是某设备故障使系统冗余度降低，卫星系统可靠性模型和失效分布参数也相应变化。因此，需要考虑随机失效分布的动态特性。

针对第1个问题，不失一般性，假设卫星已工作时间为T0，仿真产生的随机失效时间为T1，则T1必须大于T0才是一次有效仿真。当T1>T0时，卫星一次仿真中随机寿命Tr的实际值为：

Tr=T1-T0

(2)

式中：Tr、T0、T1的时间单位均为h。

针对第2个问题，当卫星未发生常驻故障、系统可靠性模型不变时，T1可以根据卫星初始寿命分布仿真得到。若卫星服从指数分布且其失效率为λ0，则卫星随机失效时间的仿真值为：

(3)

式中：η为随机数，0<η<1。

若卫星服从威布尔分布且当前的概率密度函数为：

(4)

式中：b为特征寿命，c为形状参数。则卫星随机失效时间的仿真值为：

(5)

假设卫星于T1a时刻某单机主份故障，系统组成变化如图2、图3所示。

由图3可知，卫星系统冗余度降低，系统可靠性模型改变，分别考虑指数分布和威布尔分布两种情况如下。

(1)指数分布情况

当卫星发生故障后，可以根据新的可靠性模型计算得到新的可靠度R1(Ts)，根据式(1)可得到新的失效率λ1，基于指数分布的“无记忆性”，以λ1代入式(3)求得随机失效时间值即可。

(2)威布尔分布情况

根据新的可靠性模型可拟合得到新的威布尔分布参数，此时卫星寿命分布呈现两阶段分布特征：

(6)

式中：ba、ca为卫星在T1a时刻前的威布尔分布参数；bb、cb为卫星在T1a时刻后的威布尔分布参数，根据新的可靠性模型拟合得到；T0b为第二阶段威布尔分布的位置参数，基于卫星寿命分布的连续性：

(7)

逻辑上有T0>T1a，因此，卫星随机失效时间的有效仿真值应为：

(8)

当卫星于T1b时刻再次发生常驻故障、系统可靠性模型变化时，卫星寿命分布将呈现三阶段分布特征，其分布形式和有效仿真值在式(6)、式(8)基础上依次类推。

2.2 基于消耗性物资的卫星剩余寿命

大多数卫星的消耗寿命仅取决于推进剂。考虑更一般的情况，假设有m种影响卫星寿命的独立消耗因素，则卫星消耗寿命取决于消耗最快的因素，有:

Tc=min(T21,T22,…,T2m)

(9)

式中：T2i(i=1,2,…,m)是第i种消耗因素的预估寿命，根据每种消耗因素的寿命模型计算而得。

以推进剂消耗为例，假设利用现有技术[8]预估的卫星当前剩余推进剂为X，卫星年消耗推进剂为X1～X2，卫星不可使用的推进剂残留量、离轨再捕获推进剂消耗量和计算误差量之和为Xr。并假设推进剂年消耗量呈均匀分布，根据均匀分布的蒙特卡罗抽样公式，由推进剂决定的卫星消耗寿命为：

T2=[T2a+η(T2b-T2a)]×8 760

(10)

式中：T2a=(X-Xr)/X2；T2b=(X-Xr)/X1。

2.3 基于退化失效的卫星剩余寿命

假设有n种影响卫星寿命的独立退化失效因素，则在一次仿真中，卫星退化寿命取决于退化最快的因素，有：

Td=min(T31,T32,…,T3n)

(11)

式中：T3i(i=1,2,…,n)为第i种退化失效的预估寿命，根据每种退化模型计算而得。

以太阳电池阵功率衰减为例，假设当前功率为P，年衰减率为Y1～Y2，卫星正常功率需求为P0。并假设太阳电池阵衰减率可按均匀分布处理，则由太阳电池阵衰减决定的卫星剩余寿命为：

T3=[T3a+η(T3b-T3a)]×8760

(12)

式中：T3a=(P-P0)/PY2；T3b=(P-P0)/

PY1。

3 卫星剩余寿命的仿真分析

3.1 分析约定

(1)整星寿命预测覆盖的产品范围

如前所述，卫星由退化、消耗和随机失效三类寿命特征产品组成，仅考虑其中任何一类产品都是不完整的，因此整星寿命预测不仅应考虑推进剂等消耗性物资，以及太阳电池阵、蓄电池组等产品的退化，还应考虑卫星任务相关的所有分系统和设备，包括有效载荷和平台的电子产品、机电产品、活动部件等各类产品的突发故障。

(2)复杂失效机理产品的处理

某些产品同时存在多种失效机理，例如蓄电池组既有可能由于电路缺陷突发故障，也可能由于性能衰降而失效。当没有占主导地位的失效机理时，应同时考虑多种失效机理，例如蓄电池组需同时考虑随机失效和退化失效，在分析时引入指数分布和退化模型。

(3)随机失效分布的选择

卫星随机失效一般可用威布尔分布或指数分布描述，威布尔分布的分析结果一般更准确，适用于单星剩余寿命预测等对准确度要求较高的情况，指数分布的分析过程则更简单，可用于多星星座的备份星策略等对单星随机寿命敏感性不高的情况。

3.2 多机理下的卫星寿命模型

依据卫星组成与产品寿命特征，可全面梳理影响卫星寿命的因素，并按消耗、退化、随机失效分为三类，建立树图如图4所示。

由图4可见，在系统层面卫星寿命模型体现为“或门”形式的竞争模型。在底层单元建模中，每一种消耗或退化失效因素应作为独立单元列出。随机寿命模型可以系统级可靠性模型为基础，通过去除退化单元、仅保留随机失效单元建立，通常包括各类电子设备和以指数分布/威布尔分布表征的机电设备、推进组件等。

如第1.2节所述，在整星层面可以将随机失效拟合为威布尔分布模型或指数分布模型。由此，假设卫星随机失效决定的剩余寿命为Tr，m种消耗因素决定的剩余寿命为T2i(i=1,2,…,m)，n种退化失效决定的剩余寿命为T3i(i=1,2,…,n)，则卫星剩余寿命为

Tleft= min[Tr,min(T21,T22,…,T2m),

min(T31,T32,…,T3n)]

(13)

3.3 仿真分析流程

在已知随机失效各单元寿命模型、消耗和退化规律的前提下，可以利用蒙特卡罗仿真方法进行卫星寿命预测，其仿真流程如图5所示。具体流程说明如下。

(1)设置初始条件

初始条件包括各单元寿命模型的参数值、卫星预期运行时间、仿真次数等。

(2)预估随机失效决定的剩余寿命

依据卫星当前所服从的随机失效模型，利用蒙特卡罗仿真抽样公式，产生卫星随机失效时间T1，若T1大于卫星已工作时间T0，则根据式(2)

得到该次仿真中由随机失效决定的剩余寿命Tr；若T1≤T0，则本次仿真无效，直接进入下一次仿真，再次产生T1的值。

(3)预估消耗性物质决定的剩余寿命

根据消耗性物质的消耗规律，获取每一种消耗因素的剩余寿命T2i(i=1,2,…,m)，比较并取其最小值即得到一次仿真中的消耗剩余寿命Tc。

(4)预估退化失效决定的剩余寿命

根据各种退化因素的退化规律，获取每一种退化因素的剩余寿命T3i(i=1,2,…,n)，比较并取其最小值即得到一次仿真中的消耗剩余寿命Td。

(5)确定一次仿真中的卫星剩余寿命Tleft

根据基于竞争模型的卫星剩余寿命式(13)，比较并取Tr、Tc、Td中的最小值即得到卫星在一次仿真中的剩余寿命Tleft。

重复流程(2)～(5)，进行多次仿真后，可得到有效仿真次数Ne和Ne个卫星剩余寿命值，则卫星平均剩余寿命为:

(14)

(7)计算卫星剩余寿命分布

卫星随机失效、退化失效及消耗均存在一定的不确定性，因此卫星剩余寿命的预估结果存在置信度。为了描述这一不确定性，给定统计区间间隔，统计落在每一个区间内的卫星累积到寿次数，即可得到卫星剩余寿命分布。

首先设置统计区间间隔(例如30天)，根据当前时刻至给定日期的时间区间求出统计区间数量NΔ：

NΔ=Tab/TΔ

(15)

式中：TΔ为统计区间间隔；Tab为当前日历时间至给定日期的时间区间。

然后统计落在每一个统计区间内的卫星累积到寿次数Fi，则卫星剩余寿命服从：

PT=1-Fi/Ne,i=1,2,…,NΔ

(16)

式中：PT即卫星剩余寿命为T的概率。

4 应用示例

已知某星座由6颗卫星构成，卫星设计寿命7年，部分卫星已经接近更新换代。为尽早确定备份星计划，需要预测在轨卫星剩余寿命并评估其超期服役的可能性。假设卫星随机失效服从指数分布，消耗性因素为推进剂，推进剂年消耗量为3～5 kg，退化因素为电池阵功率衰减，卫星功率需求不低于500 W，其他信息如表1所示。

由表1可见，尽管卫星固有设计一致，但随着在轨工作时间增加，各颗卫星在系统有效配置、推进剂消耗和退化情况上均出现差异。根据表1数据和本文方法，经计算得到各星预估寿命如表2所示。卫星剩余寿命分布如图6所示。

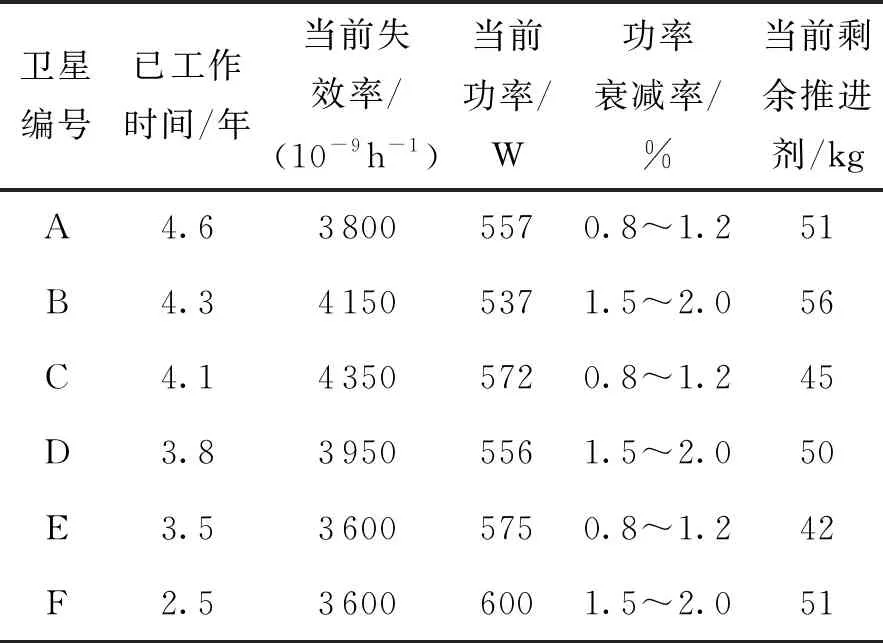
表1 卫星寿命模型有关数据

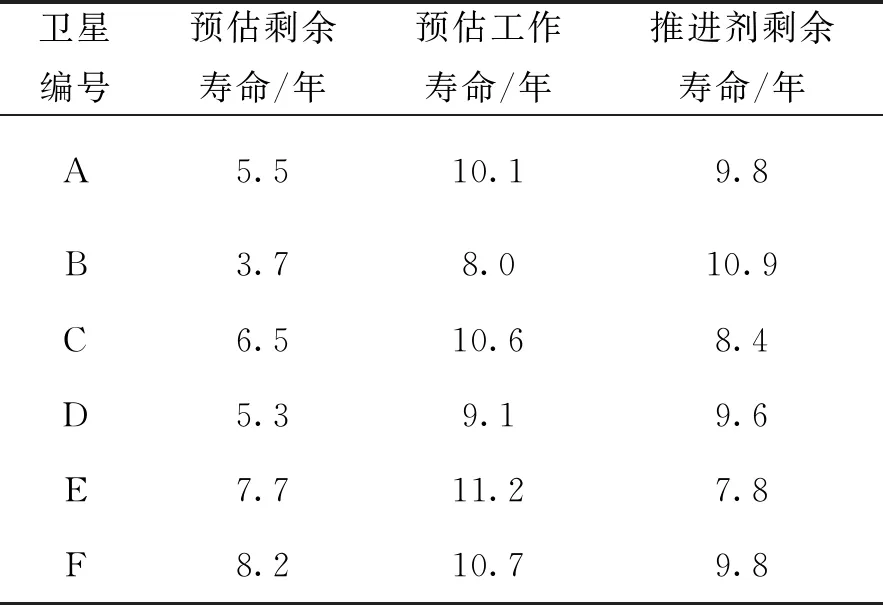
表2 预估的卫星剩余寿命(均值)

由表2、图6可见，尽管B星剩余推进剂较多、D星发射时间较晚，但这两颗卫星的剩余寿命最短，是维持星座平稳运行的薄弱环节，需提前制定替换计划；卫星剩余寿命和发射时间无必然联系，但和卫星在轨运行情况密切相关。

本文方法和基于推进剂估算方法的分析结果对比如图7所示。

由图7可见，基于剩余推进剂估算方法得到的结果均高于本文方法；个别卫星预估结果差异较大，尤其是B星，仅估算剩余推进剂时，其剩余寿命超过10年，但综合考虑星上系统工作状态、退化情况和燃料消耗，其剩余寿命均值不超过4年，显然，基于剩余推进剂估算的方法获得的结果过于乐观。

5 结束语

卫星在轨寿命终结是随机失效(突发故障)、退化失效和物资消耗三种机理作用的结果。分析卫星寿命特征，利用多机理下的寿命预测方法通过案例分析表明：

1)仅利用推进剂估算卫星剩余寿命可能得到过于乐观的结果。准确的寿命预测应覆盖随机失效、退化和消耗三类因素。

2)多机理下的寿命预测方法理论上具有更高的可信性，更适用于星座备份策略分析等工程应用。

通过多星组网运行提供连续服务是通信、导航、遥感等业务的重要实现途径。与单星任务不同，星座通常具有补网需求，准确预估卫星寿命对于星座维持和补网策略的制定具有重要意义。为获得更精确的分析结果，在各类设备的寿命变化规律和整星寿命模型等方面，仍需要开展大量研究工作。