微小卫星轨道保持的混合切换控制方法
2018-09-18,,,
,,,
1.北京航空航天大学 宇航学院,北京100191 2.北京控制工程研究所,北京100190
微小卫星具有体积小、质量小、成本低、研制周期较短等特点,而且可以进一步组成大规模卫星编队,使其在通信、对地观测等领域发挥的作用越来越大。但是在研制过程中,推进系统成为制约微小卫星技术发展的一个重要因素[1]。传统的化学推进装置以及电推进装置由于负载过重,已经不适用于微小卫星。
近年来,微机电集成技术(Micro Electro Mechanical Systems,MEMS)的出现,为研究微小卫星的新型动力装置提供了技术保障。MEMS固体微推力器阵列是一种新型推进装置,利用MEMS技术在一块芯片上集成多个可独立寻址的微推力器,与传统固、液、电推进器相比具有精度高、无燃料泄漏、冲量可调、没有其他传动部件等优点,因此受到广泛关注。国外从20世纪90年代开始展开MEMS微推进技术的研究,例如Honeywell公司和Princeton大学提出利用微推力器阵列进行微小卫星编队的相对位置保持并且已经做出兆单元推力器阵列样机[2],但是没有给出具体的控制算法;日本太空和航空科学研究所(Institute of Space and Astronautical Science,ISAS)提出将MEMS固体微推力器用于15 kg级别的月球探测器“LUNAR-A Penetrator”[3]。
国内对MEMS固体微推进研究起步较晚,目前清华大学和南京理工大学等少数高校以及北京控制工程研究所等机构已经做出样机,但是集成度较低,而且大部分研究都停留在微推力器的工艺研制阶段,对微推力器的应用研究还较少。文献[4]研究了利用MEMS微推力器阵列进行微纳卫星编队保持的控制算法,文献[5-6]研究了利用微推力器阵列抑制卫星太阳翼振动的控制算法,文献[7]研究了基于固体微推力器阵列的卫星控制一体化算法。随着微小卫星技术的飞速发展、卫星组网技术的日渐成熟,预计到2025年全球将发射微小卫星3000颗以上[8],这将会给MEMS固体微推力器阵列的应用带来广阔的应用前景[1]。
由于MEMS固体微推力器阵列是一种脉冲点火形式的推力器,在实际应用中推力持续时间短,卫星在其余时间内都是按照动力学模型自由运动,按照常规的连续推力模型建立的控制律不能准确反映脉冲推力的控制效果以及能量消耗。考虑到系统状态在有脉冲推力和无脉冲推力之间不停地切换变化,因此采用混合切换系统重新设计小卫星轨道控制律。混合切换系统可以避免直接处理复杂的非线性方程,而是将其替换为一组简单的线性方程,然后在这些简单方程之间进行切换[9]。混合切换系统的研究内容包括切换系统建模、稳定性分析和控制综合等[10-12],文献[13]研究了航天器自主交会过程的混合切换控制律,文献[14]研究了切换系统在直升机姿态控制中的应用,文献[15]提出了高超声速飞行器的混合切换控制律并进行了稳定性分析。
基于连续力轨道保持技术的缺陷以及MEMS固体微推力器体积小、质量小、单个冲量小、可以冲量组合的优点,提出一种基于混合切换系统的轨道保持模型,根据李雅普诺夫稳定性第二定理[13],建立线性矩阵不等式组,进而解得反馈控制律,并通过仿真验证了控制算法的有效性。
1 卫星动力学建模
设地球质量为M,卫星质量为m,二者距离矢量为r。则按照牛顿万有引力定律,它们之间相互吸引力的值为:
(1)
式中:G为万有引力常数。则在地心惯性系中,考虑除万有引力之外的合力为f,卫星运动方程为:
(2)
令地球引力常数μ=GM,则卫星轨道运动的基本方程写成:
(3)
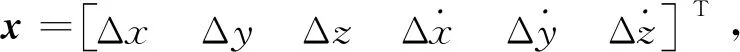
(4)
由于固体微推力器是一种间断点火的推力装置,推力器点火施加推力的时间远小于两次控制的间隔时间,且脉冲推力的量级远大于空间轨道摄动力的量级,因此,采用离散控制方法来设计卫星轨道运动模型。
如图1所示,采样间隔为τ,一个脉冲控制周期T为kτ。在脉冲推力作用之后,卫星进入自由运动阶段,直至下一次脉冲推力到来。整个过程可以视为脉冲推力阶段和自由运动阶段之间不停切换的过程。
将式(4)离散化,得到
x(n+1)=Adx(n)+Bdu(n)
(5)
式中:n=0,1,2,…为采样时刻;
(6)
根据图1可知,每次施加脉冲控制力的时刻为t0,tk,t2k,t3k,…,在每次施加脉冲后,卫星的状态量可由下式求得:
x(λk+1)=Adx(λk)+Bdu(λk),λ=0,1,2,…
(7)
在两次脉冲之间的自由运动阶段时,卫星的离散状态方程为:
x(λk+δ)=Adx(λk+δ-1),δ=2,3,…,k
(8)
式(7)和式(8)构成了卫星运动离散状态方程。整个卫星的运动过程就是由这两种状态方程之间的不停切换而构成的。
2 混合切换控制律设计
2.1 混合切换控制模型
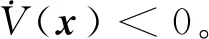
V(x(n))=xT(n)Px(n)
(9)
在每个子系统中,有
(10)
式中:P1和P2为正定对称矩阵。按照连续系统稳定判据,需要V1和V2同时满足递减。但是在自由运动阶段的子系统是一个纯开环系统,这一阶段不给航天器施加控制力,因此这个子系统的稳定性是无法保证的,V2递减的条件无法满足。所以只能通过设计V1来使得系统的李雅普诺夫函数广义递减。
按照如图2所示的能量变化,如果两个子系统的李雅普诺夫函数V1和V2能够满足:
1)V1在每个脉冲周期内都是递减的。即V1(x1) V1(x2k),V1(x3k+1) 2)每个脉冲周期内的V1的初值要比上一个周期的初值小。即V1(x0)>V1(xk)>V1(x2k)>V1(x3k)>… 3)V2在自由阶段是不可控的,但是必须在切换点处满足V1(xm) 则整个切换系统满足李雅普诺夫函数呈现全局递减趋势,即混合系统在广义条件下稳定。 对以上3个条件进一步抽象和计算: 边境包围战斗中应用伏击战法,应注意以下三点:首先,三面包围要绝对的严密,不能留有任何间隙,防止给犯罪分子留下逃跑之机,使设伏行动失去原有的效果。其次,要及时发现犯罪分子的逃跑企图,确保犯罪分子向我设伏地域逃窜,同时,包围地域到设伏地域之间的距离也不宜过长,避免距离过长从而途中出现意外,使我对犯罪分子失控,让犯罪分子有逃脱的机会;再次,确保设伏的兵力,绝对不能让犯罪分子跑出我伏击圈,要坚决将犯罪分子捕歼在我伏击地域内。 (1)ΔV1=xT(λk+1)·P1·x(λk+1)- xT(λk)·P1·x(λk)<0 对于脉冲子系统来说,有 ΔV1=[x(λk+1)]TP1x(λk+1)- [x(λk)]TP1x(λk)=[x(λk)]T· [(Ad+BdK)TP1(Ad+BdK)-P1]·x(λk) (11) 则ΔV1<0等价于 (Ad+BdK)T·P1·(Ad+BdK)-P1<0 (12) 对于V1(xλk)和V1(x(λ-1)k),有 V1(xλk)=[x(λk)]TP1x(λk) (13) V1(x(λ-1)k)=[x((λ-1)k)]TP1x[(λ-1)k] (14) 其中x(λk)可以由迭代计算来实现: (15) 则该条件可化为: (3)V1(xλk) P1-P2<0 (16) (17) (18) (19) 微小卫星在轨道保持的过程中,用于提供推力的MEMS固体微推力器总个数有限,而且如果单次脉冲推力过大的话,会直接导致轨道控制超调,造成不必要的误差和额外消耗。因此有必要针对每次施加的脉冲控制力设计限制条件。 (20) 应有|ui|≤umax,i=x,y,z。即 (21) 式中:Rx、Ry、Rz为推力矢量分割矩阵。式(21)可以等价为: (22) 引入状态反馈u=Kx,得 (23) 设存在数γ使得系统的初始能量满足V1(x0)<γ成立,即有xTP1x≤V1(x0)<γ。则式(23)成立的充分条件为: (24) 同样,根据Schur定理,式(24)可以等价为线性矩阵不等式: (25) 综上,以式(17)(18)(19)(25)共6个不等式为约束,建立LMI不等式组求得可行解X1、X2、Y1,则可解得反馈控制矩阵: (26) 仿真条件:选择立方体卫星尺寸为0.2 m×0.2 m×0.2 m。卫星质量为1 kg。采用的微推力器单位元冲量为10-4N·s。采样间隔为1 s。控制间隔为100 s。卫星运行轨道选为太阳同步轨道,轨道要素如表1所示。 表1 卫星轨道6要素 图3~图5显示了卫星三轴初始误差的控制效果和微推力器消耗情况。从仿真结果来看,本文设计的基于混合切换系统的轨道控制方法对于分米级甚至米级的初始误差都有很好的控制效果,位置误差和速度误差都是只振荡两次即可达到稳定,响应时间约为4 000 s。从推力器消耗情况来看,初始几次的消耗较多,但是均小于设定的单次最大消耗量nmax,符合预设条件。 从图6和图7可以看出,当初始误差被控制下来以后,卫星的在轨位置误差和速度误差均稳定在一个误差区间内,并且随卫星轨道周期呈现周期性变化。卫星三轴位置误差均保持在0.2 m以内,速度误差保持在0.5×10-3m/s以内。由图9可知,后期推力器消耗情况也随卫星轨道周期呈现周期性变化,而且y向推力器消耗明显低于其他两个方向。这是因为卫星摄动力主要作用在卫星的x轴和z轴方向,y向扰动很小,因此y向误差累计很慢。仿真结果显示平均每个轨道周期消耗推力器约为70个。对于集成度为每平方英寸(6.452 cm2)100×100个的微推力器阵列,在立方体卫星每个表面贴10片即可以保证小卫星在轨运行1年以上。 本文研究了基于MEMS微推力器阵列的微小卫星轨道保持问题,针对微推力器推力不连续的特点,根据李雅普诺夫稳定性定理,设计了卫星轨道保持的混合切换控制律。结果表明,所设计的控制方法对于卫星初始误差和在轨实时误差有很好的控制效果,验证了混合切换控制律的有效性,能够准确反映出MEMS固体微推力器阵列的推力特点。MEMS微推力器阵列满足微小卫星高精度轨道保持的要求,可以克服传统推进技术在微小卫星上无法应用的问题,为微推力器阵列在微小卫星轨道控制应用提供了仿真试验支持,证明这种新型推力装置具有广阔的应用前景。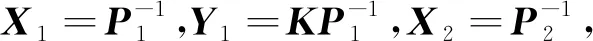
2.2 推力限制条件
3 仿真校验

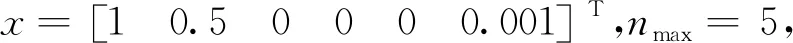
4 结束语
