区域机动目标普查监视小卫星组网设计与仿真

，，，

1.航天工程大学 研究生管理大队，北京 101416 2.航天工程大学 航天指挥系，北京 101416

海洋热点区域机动目标搜索监视在军事与民事中都有重要的应用价值[1]。相比静止点目标与区域目标，海洋机动目标由于其机动特性以及自身具有的电子静默技术等特点使得侦测任务更为困难，对航天侦察的体系和能力提出更高的要求[2]，目前针对机动目标搜索观测的研究主要通过在轨卫星任务规划完成，其中比较有代表性意义的是将海洋机动目标监视任务分为相互独立的3个阶段——搜索、定位和跟踪，并在空间监视任务共同求解框架GAMBIT的基础上对各个搜索阶段进行卫星调度规划，实现对海洋机动目标的跟踪监视[3]。文献[4-6]基于机动目标先验信息和目标运动预测技术，通过对卫星观测条带与过境窗口的选择调度，得到最优的机动目标侦察方案。文献[7]针对海洋机动目标监视问题，对匀速运动、航迹变更等多种目标运动预测模型进行了改进，针对短期监视与长期监视任务，以最大化目标发现概率作为期望收益，相比最大化区域覆盖率能够获得更好的观测效果。

从当前机动目标搜索研究现状可以看出，面向海洋机动目标的搜索主要存在两点不足：1)大多数研究都是假设已知机动目标某一时刻初始位置信息，而对于某一区域内机动目标，一般情况下很难获得其初始位置信息。2)由于目前在轨卫星在组网发射之初主要针对地面静止点目标与区域目标进行设计，若机动目标通过卫星轨道预测得知卫星过境时间窗口，便能够通过有效机动来规避卫星侦察，使得通过在轨卫星任务规划进行机动目标侦察任务非常困难。针对此问题，本文研究的内容为：假设已知某一目标区域，通过设计侦察卫星星座，弥补现有航天侦察能力缺陷，有效对目标监视区域进行普查搜索，实现以一定周期间隔对目标区域进行普查监视，判断机动目标是否进入该目标区域，从根本上解决机动目标监视困难的问题。

1 基于条带拼接的机动目标普查搜索策略

在对机动目标的搜索观测中，若卫星前后相邻过境观测条带时间分辨率相差过大，由于机动目标的机动特性，则很容易造成观测资源无效[8-9]，针对此情况本文设计了一种考虑机动目标机动特性的成像卫星普查搜索策略，在未知机动目标先验信息的情况下，通过对用户感兴趣区域进行普查观测以获取机动目标的位置信息。

已知条件：可用卫星资源集S，仿真周期内星下点经纬度集合I、目标区域R的顶点坐标、卫星星载遥感器视场角β、遥感器侧摆角范围[-λ,λ]。

步骤1) 遍历虚拟卫星资源集S每颗卫星的星下点轨迹，由目标区域R的顶点坐标{(lon1,lat1),(lon2,lat2)…(lonn,latn)}依次向sati的星下线作垂线，得到垂点集合P，由于sati的星下点经纬度集合I都包含其对应时刻，因此采用插值法求解出垂点集合P对应的时间集合T，T={t1,t2,…,tNPi}，则sati的过境时间窗口为[minT,maxT]，按照初始过境时间minT大小对过境窗口进行升序排序，筛选出首次过境卫星时间窗口Begin[minT,maxT]。对目标区域顶点经度大小进行降序排列，筛选出目标区域最东侧顶点East[lon,lat]。

步骤2) 根据首次过境时间窗口Begin[minT,maxT]，以及卫星星载遥感器视场角β、遥感器侧摆角范围[-λ,λ]，计算出首次卫星过境成像可达到观测范围，判断目标区域顶点East[lon,lat]是否能被覆盖观测，若能，跳至下一步，若不能，转到步骤6)终止算法。

步骤3) 根据目标区域顶点East[lon,lat]所对应的垂点East[Plon,Plat]，由文献[10]侧摆角度计算模型计算出首次过境卫星观测条带Strip1对应的侧摆角度θ1，计算条带Strip1对应的西侧两个顶点坐标(B1lon,B1lat)、(B2lon,B2lat)，根据B1lon、B2lon大小筛选东侧顶点East{B1,B2}，作为下一次卫星过境成像的观测目标点。

步骤4) 由第二次卫星过境窗口Second[minT,

maxT]采用步骤2)的方法判断East{B1,B2}是否在本次卫星覆盖观测范围内，若能，采用步骤3)方法计算本次观测条带对应的侧摆角度θ2，并计算出两次过境窗口时间差Δt1，Δt1=BeginminT-SecondminT，此时如果考虑卫星过境时间内目标机动，还需要计算单次过境窗口时间差Δt2，Δt2=SecondmaxT-SecondminT。由此得到时间差Δt=Δt1+Δt2。区别于静止区域普查条带拼接，观测目标为机动目标进行条带拼接时，设第i+1次卫星过境时间与第i次卫星过境时间差为Δti，机动目标最大机动速度为vmax，则第i+1次卫星过境时需要保证条带重叠宽度为vmaxΔti，以此来保证条带观测的有效性。由此更新i+1次卫星观测角度：

(1)

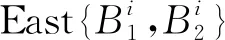
步骤5) 由于地球自西向东的自转特性，重复步骤2)至步骤4)的方法对目标区域从右向左依次进行条带扫描地毯式搜索观测，直至完成对目标区域最左侧顶点的覆盖观测，如图1所示。

步骤6) 终止算法。

机动目标普查搜索策略对虚拟卫星资源集S的时空特性有着严格要求。在时间分辨率上，要求相邻两颗过境卫星观测时间不能大于侦察目标机动一个成像幅宽距离的时间，否则前一个观测条带便失去其观测意义。在卫星空间位置分布上，要求卫星在过

境观测时，成像条带之间要平行或相对平行，方便条带之间拼接组合。由于卫星在进行区域目标成像时一般采取推扫模式，成像条带平行于卫星星下点轨迹，因此对卫星空间位置分布要求可转换为对虚拟卫星资源集S的星下点轨迹要求[11]。当虚拟卫星资源集S中每颗卫星过顶目标区域时星下点轨迹能够以一定间隔平行分布，则能够实现本文机动目标动态搜索策略。同时，该动态区域目标观测方法采用立体几何在球面进行解析求解，避免了传统区域目标分解方法频繁的坐标、投影转换对计算精度以及计算效率的影响，对任意目标区域形状都有较好的适应性。

2 面向移动目标普查监视的星座构型设计与优化

2.1 星座构型与目标函数的建立

由第1节模型分析可得知，面向区域机动目标普查监视的小卫星组网需要在过境观测时多星之间星下点轨迹平行或相对平行，并且相邻卫星过境窗口时间差不能太大，以便于在时空约束条件下对机动目标实现拼接搜索。针对此任务需求，考虑卫星组网发射成本问题(轨道面越少成本越低)，采用卫星同轨组网方法，设计了一种面向区域覆盖的高时间分辨率普查监视组网星座构型，以此满足机动目标普查监视搜索策略。

如图2所示，组网卫星采用一定相位角分布在同一轨道上，并且星下点轨迹在经过目标区域时相对平行，能够有效满足任务的高时间分辨率及星下线约束要求。通过对该组网星座构型分析可知，当星座中各颗卫星相邻较近时(星与星之间相位较小)，组网卫星星下线轨迹相对“密集”，此时进行机动目标普查监视搜索则需要组网各颗卫星进行大幅度的姿态角度调节才能完成拼接策略。当组网卫星相位分布较大时，此时星与星之间星下线相对“分散”，卫星只需进行小范围姿态调节就能够完成普查任务，但同时也增加了卫星任务执行时间，降低了卫星资源使用效率。因此本文将根据此星座构型，采用太阳同步圆轨道进行仿真设计优化，卫星组网优化变量为卫星轨道要素(a,e,i,Ω,w,u)。根据任务的重复侦察特性，增加回归轨道特性约束条件，利用回归轨道回归系数k，及回归天数D,可求解出卫星轨道半长轴a，由太阳同步轨道特性可确定轨道倾角i，由此确定组网优化设计决策变量为Ω,u1,u2,…,un。

组网设计优化目标函数有3个：最大任务观测覆盖率、最小侧摆角度总和及最小任务执行时间。对于普查成像，任务观测覆盖率通常要求达到100%，因此将任务观测覆盖率作为约束筛选条件；侧摆角度总和决定了成像质量、卫星星上能量消耗、机械损耗寿命，并且当目标区域变动时，组网卫星仍能够通过侧摆姿态调节完成任务，具有较强的鲁棒性[12]；总任务观测时长影响条带拼接余量，决定了资源利用效率[13]。综上，为评估每次组网任务的适应度[14]，定义目标收益函数F,F主要有两种决策偏好：1)面向成像分辨率、能量消耗约束要求的Fθ(观测目标中心点距星下线距离最小，即卫星所需要进行姿态调节的角度最小)；2)面向资源利用率约束要求的Ft(条带拼接余量最少，组网卫星的平均过境时间差最小)。

(1)观测分辨率偏好Fθ

观测分辨率偏好[15]Fθ可表示为:

(2)

式中：θi为卫星si的侧摆角度。当组网卫星侧摆角度全部为0时，此时卫星能量消耗、姿态调节幅度最小，成像分辨率质量最好。

(2)资源利用率偏好Ft

资源利用率偏好[16]Ft取决于多星进行成像条带推扫重叠拼接时的拼接余量，这个决策偏好希望通过减少成像条带之间的重叠拼接来提高卫星资源利用率。

(3)

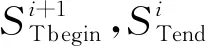
将两个决策偏好联立，得到任一组网模型的适应度评估函数maxF：

(4)

式中：a、b为决策偏好系数；n为组网观测小卫星数量。

2.2 基于遗传算法组网优化步骤

步骤1) 参数初始化。种群规模Np，交叉概率CR,进化代数Itermax，仿真周期以及监视目标场景信息。采用随机均匀分布样本生成方法在决策变量空间内生成Np个染色体xi(g)。

步骤2) 目标函数值计算。根据机动目标普查监视搜索策略计算当代个体目标函数值F，将个体携带信息值放入种群历史信息库HPOP,筛选记录最优个体xbest(g)。个体目标函数值F计算步骤为：

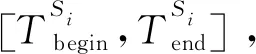
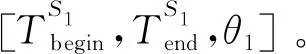
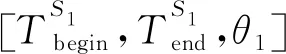
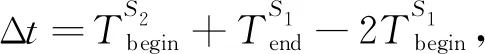
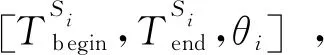
步骤4) 选择操作。根据最优保存策略执行选择操作，获得下一代种群。

步骤5) 判断是否达到最大迭代次数Itermax，如果达到，则输出。如果没有达到，则重复步骤2)～4)。

3 仿真示例分析

仿真场景从2020-01-01 00:00:00开始，待观测目标区域顶点经纬度坐标为(13.73，112.81)(13.52，119.42)(21.09，119.41)(21.09，113.54)，任务需求观测频率为至少每天一次。根据文献[17]中范艾伦辐射带及大气阻力对近地轨道卫星的影响，将卫星转移轨道高度限制在[200 km,1 500 km]，由回归轨道约束条件确定符合要求的轨道半长轴为916.1 km，根据太阳同步轨道约束条件确定轨道倾角为99.10°，为增加卫星过境观测频率，将卫星轨道设计为晨昏轨道。限制首次成像窗口范围为[06:00,07:00]。针对海洋机动目标普查任务特点，参与组网观测的小卫星分辨率可适当放低，而增大卫星成像观测条带的幅宽，本文中卫星载荷基本参数参考德国快眼AG公司RapidEye普查监视卫星[18]，组网卫星基本参数设置如表1所示。

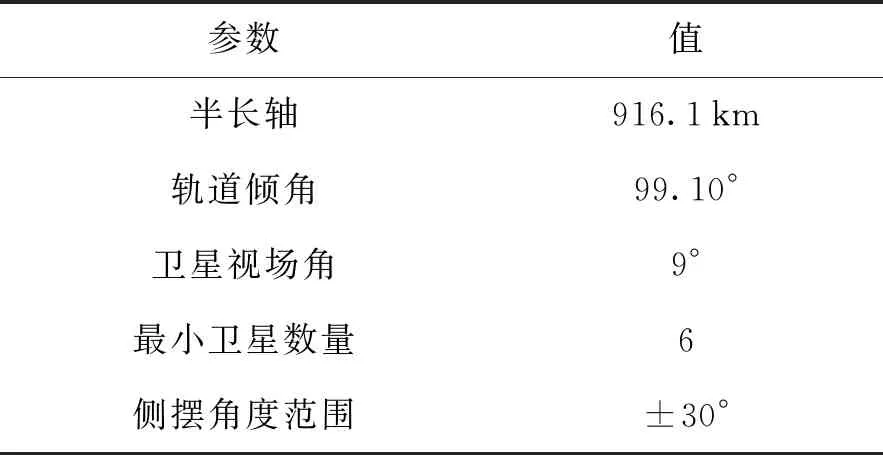
表1 组网卫星基本参数设置

机动目标最大机动速度设为60 km/h，相邻卫星最大相位差不超过35°，同时为避免相邻卫星相位接近造成卫星姿态调节过大，限制相邻卫星相位差大于5°，决策偏好系数a=0.8，b=0.2。考虑J2项摄动下利用Matlab仿真环境得到优化收敛结果如图4所示，可以看出优化模型在第43代收敛到最优解。表2与表3分别给出了图3中最优解对应的组网方案参数及相应调度信息。

参数值/(°)升交点赤经44.36真近地点角49.97/29.86/9.87/345.21/327.51/306.18

从表3中可以看出，本文设计的卫星组网方式能够在一天之内对目标区域观测两次，观测时间段分别为06:20:46—06:51:46、17:43:05—18:13:35，利用STK仿真工具可验证卫星在两个时间段内均能够100%对目标区域进行观测，并且卫星条带选择调度时考虑了侦察目标的机动特性，只要机动目标在目标区域内，无论目标采取怎样的规避方式，都无法逃避卫星监视。为验证本文组网方式有效性，将该组网方式与目前应用较广的Walker-δ星座(6/3/2)进行对比，卫星基本轨道参数与载荷性能均一致，对比结果如表4所示。可以看出，在平均访问间隔上，本文组网星座采用单轨道面，卫星访问间隔得到有效提升，并且能够做到一天之内两次100%覆盖目标区域，而Walker-δ星座累积覆盖率为136%，并且卫星过境观测时间在一天之内不规则分布，无法满足机动目标监视任务的高时间分辨率要求。Walker-δ星座在一天之内能够覆盖目标区域9次，且其中有4次观测是在夜间成像，不满足观测需求条件。综上分析可以看出，本文设计的星座能够有效解决区域机动目标监视问题，具有一定的应用价值意义。

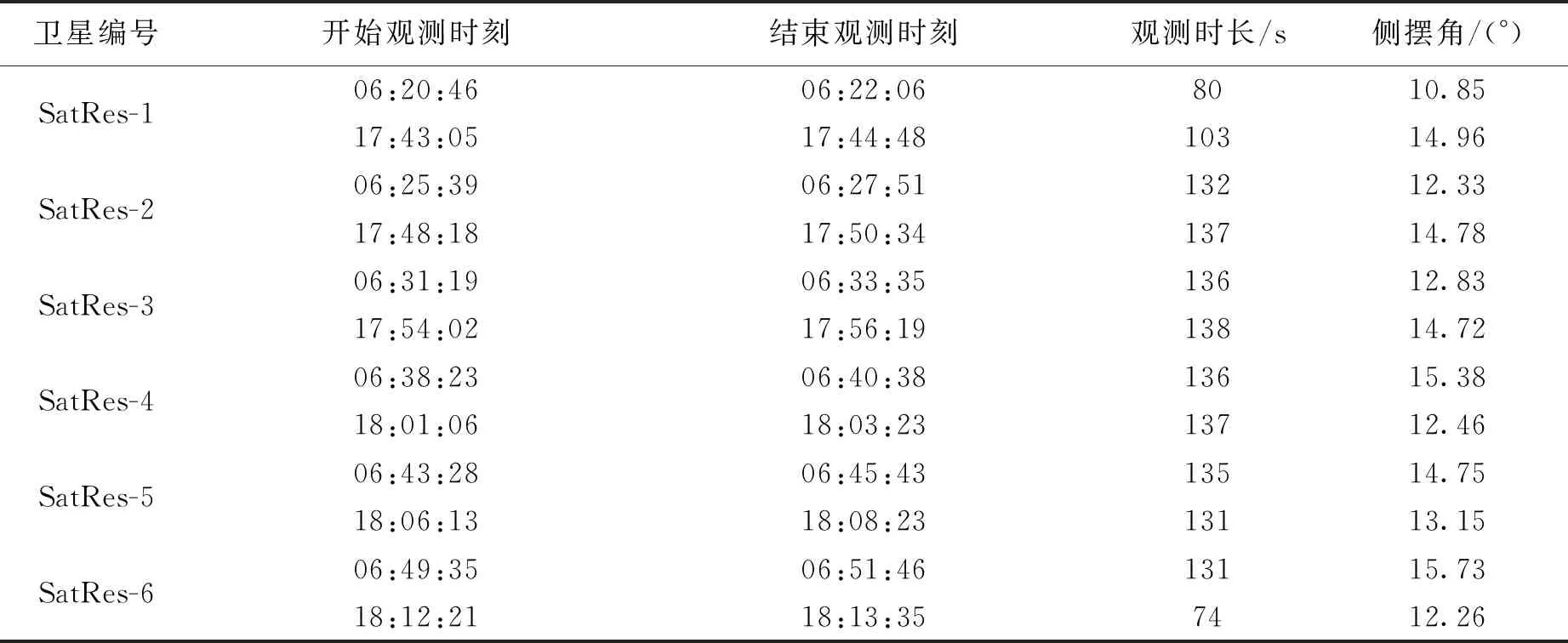
表3 组网方案对目标区域的调度信息

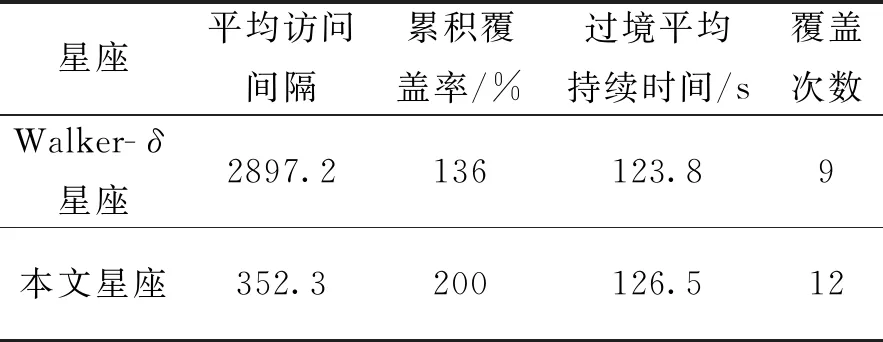
表4 组网方案覆盖性能对比

4 结束语

区域机动目标的搜索监视是侦察卫星面临的新任务，需要组网卫星具有高时间分辨率同时保持特定空间构型来对其进行观测，本文通过对机动目标搜索问题进行分析建模，建立了一种基于卫星观测条带拼接的机动目标普查搜索策略，并在此基础上设计了相应的组网卫星星座构型，通过将卫星调度与星座设计结合构造目标函数，并采用遗传算法求解得到组网卫星轨道最优部署方案。相比Walker-δ星座，该组网方案在针对区域机动目标监视问题上更加有效，可为海洋机动目标监视问题和实际工程应用提供一定参考。