加工误差对2维叶型损失系数影响的数值分析

李超东，朱家友

（中国民用航空飞行学院航空工程学院，四川广汉618307）

0 引言

压气机叶片是现代喷气发动机性能好坏的关键，经过多年的研究和设计，压气机叶片已经具有很精细的气动几何形状。尽管加工技术方面的巨大进步使得叶片的加工精度越来越高，然而由于加工公差和误差的存在，实际加工出来的叶片往往会偏离原始的设计形状和尺寸，导致压气机气动性能下降。但是由于受加工工艺的限制，减小加工公差和误差的措施需要较大的投入。如果在发动机叶片的设计阶段，能够考虑到加工误差对叶型和气动性能带来的影响，将会有效提高设计能力，缩短设计、试验、制造的周期。因此，设计人员总是在向着可以设计出对于加工公差和误差更不敏感的叶型这一方向努力。Garzon等[1]发展了1套概率论的方法去量化几何加工误差对于压气机叶片气动性能的影响；Garzon[2-3]还提出了1种从设计叶型到实际叶型的转化方法；文献[4-5]通过数值模拟研究了如何提高压气机叶片对加工误差的鲁棒性；在国内，高丽敏[6]采用单因素法数值研究了叶片扭转、轮廓度加工误差对叶栅气动性能的影响，表明不同位置、不同大小的误差对性能影响不一；文献[7-9]深入研究了叶型前缘对压气机性能的影响。

本文结合行业标准中对叶型公差的规定，在满足公差要求的基础上，发展了1套简便可行的误差函数，用以获得考虑加工误差后的压气机叶片的实际叶型，并且对考虑加工误差后的实际叶型的性能开展研究。

1 实际叶型的生成方法

《中华人民共和国航空工业标准-叶片叶型的标注、公差与叶身表面粗糙度》（HB5647）[10]对叶片的公差等进行了详细规定。假设符合设计公差和粗糙度要求的叶片就是实际中使用的叶片，也作为本文数值模型的对象。

HB 5647对平面叶栅的公差要求有2个：轮廓度公差和轮廓度变化率公差。轮廓度公差主要控制叶型增厚和减薄的程度，轮廓度变化率公差主要控制叶型的波纹度和局部的轮廓度。

轮廓度公差是指实际叶型偏离设计叶型的尺寸，如图1所示；任意2个相同方向的局部轮廓度误差的差值（取绝对值）或任意2个不同方向的局部叶型轮廓误差与其对应的理想叶型上2点间的型线长度之比，成为轮廓度误差的变化率，简称叶型轮廓度变化率。

图1 轮廓度公差的定义

轮廓度公差δy（见表1）根据叶型的弦长给出，叶型的弦长为16.86 mm，对应不同精度等级的δy分别取 0.12、0.10、0.08、0.06 mm。HB 5647 中规定轮廓度变化率分别取为2.0δy/b，b为叶型弦长。

由于缺乏实际叶型偏离设计叶型的数据，并且在下文的研究中将主要进行统计分析，所以每种实际叶型偏离设计叶型的具体形式并不重要。在这种情况下，可采用1个简单的函数来模拟实际叶型偏离设计叶型的情况

表1 叶型轮廓度公差

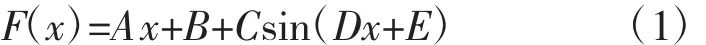
A、B、C、D、E都由随机数给出。由于在前尾缘位置处需要满足一定条件，所以5个参数并不完全独立。只要F（x）、F'（x）分别满足轮廓度公差和轮廓度变化率公差的要求，就认为该种实际叶型偏离设计叶型的情况在实际工程中是可能出现的。选择其中满足公差要求的结果作为后续输入。典型的F（x）的分布如图2所示。

图2 典型的F（x）分布

将F（x）叠加到设计叶型中，可以得到实际叶型（如图3所示），用于下一步计算和分析。

图3 典型的实际叶型轮廓（黑色为设计叶型）和前、尾缘放大

2 实际叶型的气动性能

在轮廓度公差为0.12 mm的情况下生成100种实际叶型，采用2维CFD程序MAP计算每种实际叶型的气动性能和流场，该程序在压气机流场的数值模拟中具有优秀的准确性，得到广泛应用[11-12]。

计算的一部分实际叶型以及设计叶型的攻角特性如图4所示。从图中可见，实际叶型中性能提高和降低的叶型各占50%，下文的分析也能进一步证明。

图4 部分实际叶型的攻角特性曲线

3 实际叶型的设计参数

从以上分析可知，实际叶型的气动性能发生了明显变化，而前尾缘半径、进出口金属角、最大厚度及其位置、最大挠度及其位置都会对叶型的气动性能产生影响。下文将对实际叶型的设计参数开展研究，对比加工误差对叶型的设计参数带来的变化。文献[13-15]对叶片的Bezier曲线拟合进行了研究。

对1个轴流叶型的中弧线和最大厚度采用4阶Bezier曲线拟合（如图5所示）。

图5 Bezier曲线拟合方法

确定中弧线的参数和最大厚度的参数分别有11个，所以，用于拟合叶型的可变参数有22个，另外还有5个不变参数。

具体拟合过程如下：

（1）读入原始离散叶型，确定离散叶型的前尾缘中心点位置，如果原始离散叶型有前尾缘则将前尾缘去掉，重新分布叶型上的离散点；

（2）计算或估计叶型的各参数化参量的值，将叶型以弦长无量纲化，旋转叶型到零安装角；

（3）采用DFP寻优方法确定参数化叶型22个可变参数的值；

（4）通过22个可变参数和5个固定参数给出叶型的设计参数。

采用该方法分别计算100种实际叶型的设计参数。

4 结果分析

4.1 统计分析

通过前面的计算，得到了100种实际叶型的气动性能和设计参数。对每种叶型的最小损失系数进行分析，考虑其分布形式。最小损失系数的分布如图6所示。从图中可见，最小损失系数的分布近似呈正态分布。最小损失系数的正态P-P如图7所示。从图中可见，空心坐标点与直线越吻合表明最小损失系数的分布越接近正态分布。

图6 最小损失系数的分布

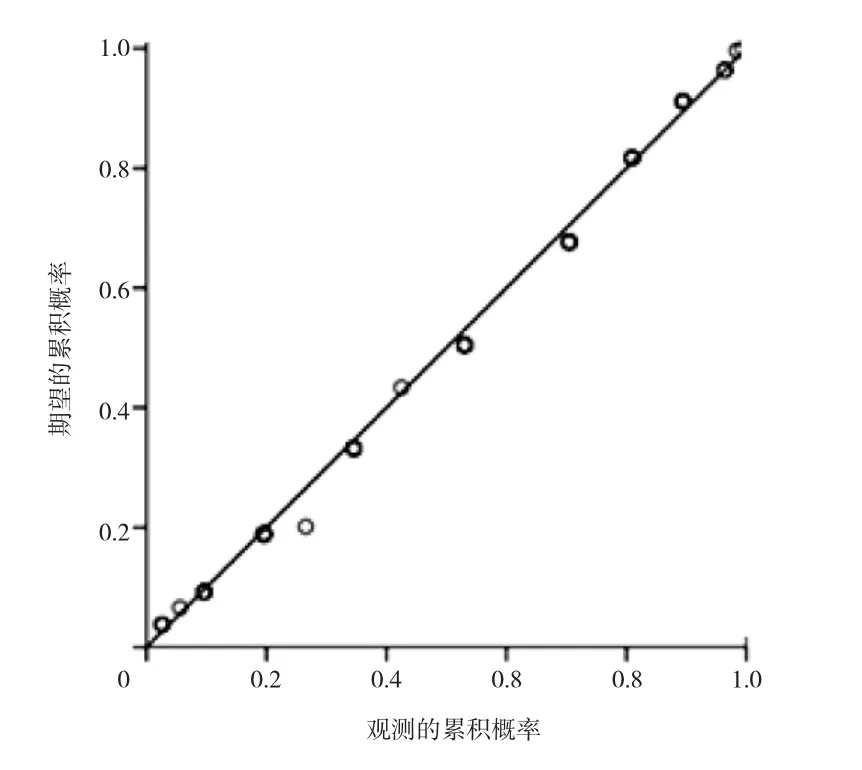
图7 最小损失系数的正态P-P

实际叶型的最小损失系数和各设计参数的统计量的均值和标准差见表2，并与原始叶型进行比较。

表2 最小损失系数和部分设计参数的均值以及标准差

从表中可见，实际叶型最小损失系数的均值比设计叶型的降低了0.67%，与采用的设计叶型有关，该叶型是从某4级压气机的第4级静子叶中部分取出的，可能叶型在设计时更多考虑的是多级匹配的问题，而不是把损失系数设计为最小。

整体上来看，各统计量的均值偏离原始叶型的程度都不是很大，可以认为二者近似相等。

采用正态分布的“3σ原则”对最小损失系数进行分析得到以下结论：

（1）最小损失系数落在（1.37%，1.82%）内的概率为68.3%，此时最小损失系数变化最大为11.8%；

（2）最小损失系数落在（1.15%，2.04%）内的概率为95.4%，此时最小损失系数变化最大为23.6%；

（3）最小损失系数落在（0.93%，2.27%）内的概率为99.7%，此时最小损失系数变化最大为35.4%。

也就是说，对于该设计叶型来说，考虑到加工误差后，实际叶型的气动性能并没有很大恶化，可以满足实际压气机的工作需要，从另一方面表明前文给出的获得实际叶型的方法是可行、符合实际的。

4.2 相关性分析

实际叶型的气动性能虽没有很大恶化，但还是产生了一些变化，而很多设计参数都会对气动性能产生影响，因此需要知道导致气动性能变化的最主要原因。所以，在上文基础上开展了相关性分析。

相关系数是用以反映变量之间相关关系密切程度的统计指标

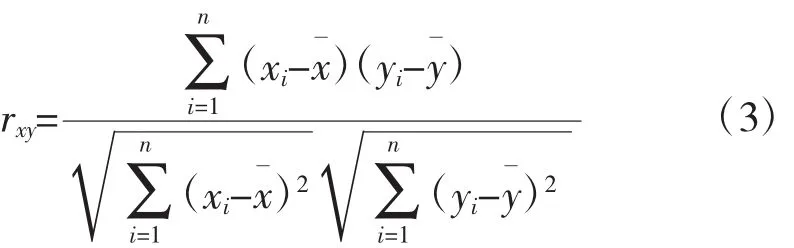
通过计算可以得到最小损失系数与设计参数之间相关系数的值，见表3。在统计学上认为，当相关系数超过0.75时，认为2个变量有很强的相关关系。而最小损失系数和最大厚度以及前缘半径的相关系数都超过了0.82。

表3 最小损失系数和部分设计参数的相关性分析

最小损失系数与最大厚度、前缘半径之间关系分别如图8、9所示。从图中可见，最小损失系数与最大厚度、前缘半径之间呈现比较明显的线性关系，以此为基础进行下一步分析。

图8 最小损失系数与最大厚度相关性分析

4.3 公差大小对设计参数和气动性能变化的影响

图9 最小损失系数与前缘半径相关性分析

上文所有的研究和分析都是在轮廓度公差为0.12 mm的情况下进行，接下来把公差分别设定为0.06、0.08、0.10 mm，重复上文的研究。只是此时不再进行气动性能的2维CFD计算，根据上文的研究结论，同样可以给出每种公差下实际叶型气动性能的正态分布曲线，也就是求出每种情况下的均值和标准差。

由于不需要进行2维CFD计算，可以把样本数取得更多，在每种公差下均生成400种实际叶型用于设计参数计算和分析。

采用上文4阶Bezier曲线拟合方法的实际叶型的设计参数进行计算，可找到最大厚度的变化。不同公差下最大厚度的分布和直方图分别如图10、11所示。从图中可见，当公差变小时，最大厚度的变化仍然符合正态分布，并且均值不变，但是最大厚度的离散程度明显变小，也就是标准差变小。

图10 不同公差下最大厚度的分布

由于最大厚度的均值不变，可以认为公差变小时，最小损失系数分布的均值保持不变。

上述研究表明最小损失系数与最大厚度之间有很强的线性关系。统计学上的分析可以证明：当2个统计量x和y呈线性关系y=kx+b时，二者之间的标准差满足 σy∶σx=k2。

图11 不同公差下最大厚度分布

但是考虑到最小损失系数与最大厚度之间并不是完全的线性关系，加上修正之后可以认为在每种公差下最小损失系数分布的标准差与最大厚度分布的标准差之比等于某定值，据此可以计算出轮廓度公差为0.06、0.08、0.10 mm时最小损失系数分布标准差，见表4。

表4 不同公差下的最大厚度和最小损失系数的标准差

其中，轮廓度公差为0.12 mm下，最小损失系数的标准差由2维CFD计算后经过统计学分析得出，在此处作为基准，其他3种公差下的最小损失系数是未经2维CFD计算预估出的。

此时可以做出每种轮廓度公差下最小损失系数的概率密度函数（如图12所示），对于叶型的设计和评估具有重要意义。

图12 不同公差下最小损失系数的概率密度函数f（x）

概率密度函数f（x）具有如下性质

进而通过概率密度函数f（x）可以很容易地求出最小损失系数在每个区间内出现的概率。根据对叶型气动性能的要求，在设计叶型以及进行加工工艺设计时可以在气动性能和加工成本之间找到平衡，确定最合适的轮廓度公差，从而确定最具性价比的设计和加工工艺。

5 结论

（1）给出了1种简单可行的从设计叶型到实际叶型转化的方法，研究表明该方法简单可行且符合实际；

（2）对于该设计叶型来说，最大厚度与前缘半径的变化是导致实际叶型气动性能变化的最重要原因；

（3）给出了1种在较小工作量所有轮廓度公差下气动性能变化的概率密度函数的方法，对于叶型设计和评估具有重要意义。