3自由度等刚度永磁弹簧的尺寸参数特性研究

孙 凤，张 明，孙兴伟，金嘉琦

（沈阳工业大学，辽宁 沈阳 110870）

1 引言

永磁弹簧是利用永磁体间的磁力实现金属弹簧性能的磁弹簧。永磁弹簧具有设计安装简单、耐老化、耐高温等特点。与常见的金属弹簧，液体或气体为介质的弹簧相比，它解决了弹簧断裂、弹簧松弛、油封漏油等诸多问题，特别适合于真空、高速、核电和超洁净等特殊的应用场合[1-3]。例如某学者将磁弹簧减震器应用于行星轮式月球车的减震系统中，没有严格的密封要求，很好的适应了高度真空的月球表面环境，克服了现有以液体或气体为工作介质的减震器的工作局限性[4]。某学者在液压元件方面，充分利用永磁弹簧的特点进行了积极的探索，利用永磁体间的吸引力对永磁式单向阀、永磁式卸荷阀进行了相关研究，研究发现，永磁弹簧式单向阀和永磁弹簧式溢流阀具备响应快、压力损失小、体积小等优点[5]。

在分析了环形永磁体和柱形永磁体及气隙磁导的基础上，提出了一种径向为工作方向的3自由度等刚度永磁弹簧，该永磁弹簧的性能主要是由相互作用的永磁体决定的。为明晰该永磁弹簧的尺寸参数特性，运用大型有限元软件ANSOFT对稀土永磁弹簧的力学特性进行数值模拟分析。影响永磁体间相互作用的因素归纳起来主要有以下几点：环形永磁体的平均半径和轴向长度、柱形永磁体的半径和轴向长度、环形永磁体和柱形永磁体竖直方向气隙的长度。这些因素对磁弹簧力学性能都有不同程度影响。为此就稀土永磁弹簧的径向回复力与位移的关系和永磁弹簧的尺寸参数的关系进行了有限元模拟分析和实验分析，并将有限元模拟结果与实验测量值进行比较，通过对比发现：有限元数值模拟能较准确地反映稀土永磁弹簧在实际工作时的力学特性。

2 结构及工作原理

设计了由下底，环形永磁体，平面球轴承，柱形永磁体和上盖组成的3自由度等刚度磁弹簧装置，如图1所示。柱形永磁体和环形永磁体同级，同心相对，每个柱形永磁体和环形永磁体为一组，设置多组，且多组永磁体沿上盖和下底的中心均匀对称安装于下底和上盖的凹槽上。将去掉一个轴承端盖的平面球轴承沿下底和上盖的中心均匀对称安装在下底的凹槽上，永磁体和平面球轴承穿插设置。永磁体设置3组，3组是达到稳定支撑和3自由度等刚度的最小组数。平面球轴承支撑上顶和下盖使柱形永磁体和环形永磁体在轴向方向上形成一定气隙，如图1（b）所示。每组永磁体间在水平方向上表现为斥力，在竖直方向上表现为吸引力，这样永磁弹簧的上盖和下底间在轴向方向上形成一定刚度，上盖在轴向方向上不会发生窜动，此种布置的永磁弹簧，在平动平面内，可以沿着x方向，y方向移动和c向转动。沿x方向，y方向移动和c向转动的位移量相等则受到的回复斥力相等，即沿x方向y方向移动和c向回转的刚度系数相等。当上盖与下底沿中心水平方向平动或转动时环形永磁体和柱形永磁体在水平面内的磁力随着位移增大而增大。最大位移量为环形永磁体内半径与柱形永磁体半径的差[6]。

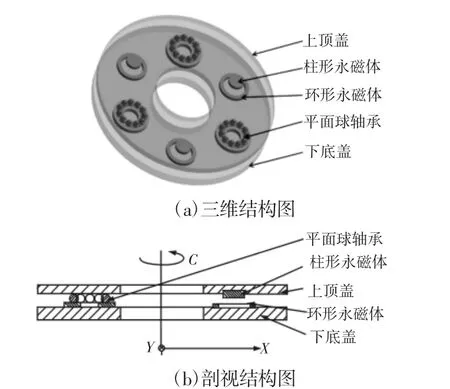
图1 3自由度等刚度磁弹簧结构Fig.1 Structure of 3 Degrees of Freedom Same-Stiffness Permanent Magnetic Spring

3 尺寸参数特性分析

稀土永磁弹簧在实际工作中，由于漏磁和尺寸参数等各种因素的影响。其工作特性与计算模型之间的误差较大，虽然文献[8]中给出了计算修正方法，但得出修正系数需要消耗大量的财力与人力资源，这些因素制约了理论研究的深入及产品推广。而有限元数值模拟具有节省费用、缩短研发产品周期、不受外部环境因素影响等特点，为此，首先采用有限元元件ANSOFT对稀土永磁弹簧的力学尺寸参数特性进行数值模拟。首先建立该系统的结构模型。由于该系统由3组结构完全相同的柱状永磁体和环形永磁体构成。首先建立一组永磁体的模型，如图2所示。阐明各参数变量的意义。

3.1 有限元分析

由于有限元数值模拟能比较直观、准确地反映出稀土永磁体之间的作用力，同时能直观地描述出永磁体在工作过程中的磁力线分布图、磁通密度矢量图等，故利用ANSOFT的三维建模环境Maxwell 3D建立有限元模型，具体建模过程如下：（1）根据永磁弹簧一组永磁体的结构参数，如图2、表1所示。参数建立的有限元仿真物理模型，如图3所示。（2）确定单组永磁体的材料属性3、确定有限元计算的边界条件和外源参数4、网格剖分5、设置求解参数，进行计算[7-10]。

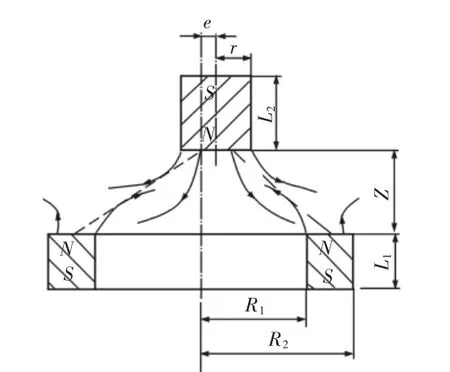
图2 一组永磁体的结构参数Fig.2 Structural Parameters of the Permanent Magnet

表1 单组永磁体参数Tab.1 Parameters of a Group of Permanent Magnet

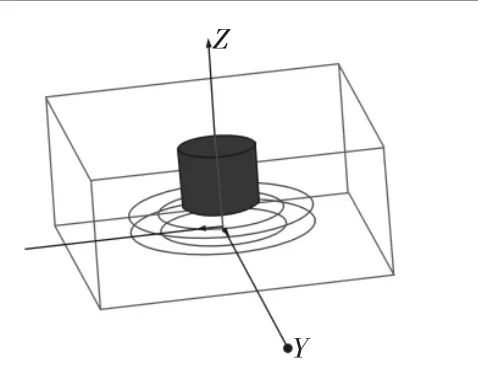
图3 单组永磁体仿真结构图Fig.3 Structural Parameters of the Permanent Magnet

将表1中的参数作为仿真计算的公用值，分别改变径向位移、轴向气隙长度、柱形永磁体半径和轴向长度，环形永磁体平均半径和轴向长度，代入事先建立好的ANSOFT参数化有限元仿真模型，进行仿真计算，分析径向磁力与上述参数之间的关系。

3.1.1 径向磁力与轴向位移z和径向位移e的关系

钕铁硼永磁材料为N30，结构参数，如表1所示。柱形永磁体和环形永磁体结构参数不变，柱形永磁体和环形永磁体间的径向位移e从（0～5）mm，柱形永磁体和环形永磁体轴向气隙z从0.5mm变化到5mm。代入有限元分析软件得到计算结果。径向磁力与径向位移和轴向位移的关系，如图4所示。径向磁力随着径向位移e的增大而增大，径向磁力随着轴向位移z的增加近似呈抛物线趋势变化先缓慢增加然后减小。

3.1.2 径向磁力与柱形永磁体半径r和轴向长度L2的关系

钕铁硼永磁材料为N30，结构参数，如表1所示。环形永磁体结构参数不变，柱形永磁体和环形永磁体间的轴向气隙z=0.5mm，柱形永磁体和环形永磁体间的径向偏移量e=2mm，柱形永磁体长度L2从8mm变化到15mm。将柱形永磁体半径r从7mm变化到12mm，代入有限元分析软件进行有限元分析。径向磁力与柱形永磁体的长度和柱形永磁体的半径的关系，如图5所示。可见，径向磁力随着柱形永磁体轴向长度的增加近似呈线性关系增加，径向磁力随着柱形永磁体半径的增加近似呈幂指数关系增加。可见在其它参数不变的情况下，柱形永磁体的半径对径向磁力的影响比柱形永磁体的轴向长度对径向磁力的影响要明显的多。

3.1.3 径向磁力与环形永磁体平均半径R和轴向长度L1的关系

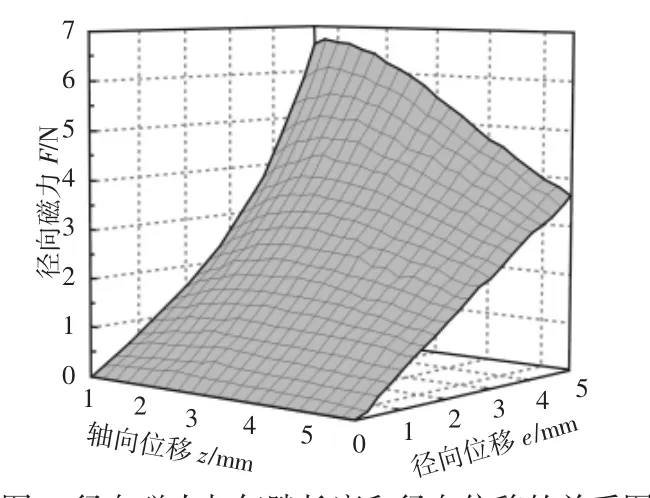
图4 径向磁力与气隙长度和径向位移的关系图Fig.4 Relationship Between Radial Magnetic Force and Axial Displacement and Radial Displacement

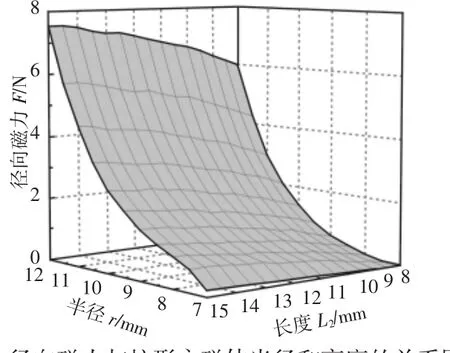
图5 径向磁力与柱形永磁体半径和高度的关系图Fig.5 Relationship Between Radial Magnetic Force and the Radius and Height of Cylindrical Permanent Magnet

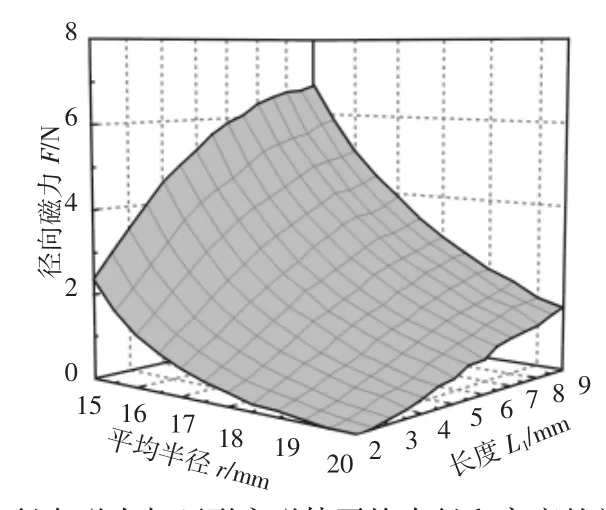
图6 径向磁力与环形永磁体平均半径和高度的关系图Fig.6 Relationship Between Radial Magnetic Force and the Height and Mean Radius of Annular Permanent Magnet

钕铁硼永磁材料为N30，结构参数，如表1所示。柱形永磁体结构参数不变，柱形永磁体和环形永磁体间的轴向气隙z=0.5mm，柱形永磁体和环形永磁体间的径向偏移量e=2mm，保持环形永磁体的外径和内径差R2-R1=6mm不变，设置环形永磁体平均半径R=0.5（R2+R1），环形永磁体平均半径R从15mm变化到20.5mm，环形永磁体轴向长度L1从2mm变化到9mm。代入有限元分析软件进行有限元分析。径向磁力与环形永磁体的平均半径和轴向长度的关系，如图6所示。可见，径向磁力随着环形永磁体轴向长度的增加近似呈幂指数关系增加，径向磁力随着环形永磁体平均半径的增加逐渐减小。可见在其它参数不变的情况下，环形永磁体的轴向长度对径向磁力的影响比平均半径对径向磁力的影响要明显的多。

3.2 实验研究

3.2.1 实验平台

试验台照片，如图7所示。图中，1为z向一自由度微动平台，量程为13mm，精度为0.01mm；2为铝合金型材搭建的龙门框架；3 为力传感器，型号为 Load Cell CXZ-114，量程为（0～300）N，精度为0.01N；4为柱形永磁体；5为环形永磁体；6为xy方向两自由度微动平台，量程为13mm，精度为0.01mm；7为力值显示控制仪，型号为XSB-I。xyz3个方向的微动平台可以实现柱形永磁体和环形永磁体的对中，可以从微动平台上读出径向相对位移量，从力值显示控制仪上读出径向磁力。

图7 径向磁力测量实验台Fig.7 Measurement Experiment System of the Radial Magnetic Force

3.2.2 径向偏移量的对比分析

实验中，永磁体材料NdFeB N30，永磁体剩磁Br为1.08T，永磁体矫顽力Hc为-796000 A/m，空气磁导率μ0为4π×10-7H/m，（BH）max取223kJ/m3，环形永磁体内径R1为14.5mm，环形永磁体外径R2为20.5mm，柱形永磁铁长度L2为14mm，环形永磁铁长度L1为4mm，柱形永磁体半径r为9mm，柱形永磁体和环形永磁体间的轴向气隙z=0.5mm、将径向偏移量e从（0～4）mm每次增加0.25mm。得到径向磁力的实验值。如上条件的实验结果与相同条件下的仿真结果对比呈现，如图8所示。由图8可以看出，在上述实验条件下，永磁弹簧的径向磁力随径向位移增加近似呈线性关系关系增加。大径向偏移时误差偏大，这主要是由环形永磁体和柱形永磁体间实际漏磁随径向位移增大而也越来越大。

3.2.3 永磁体长度参数的对比分析

实验中，永磁体材料NdFeB N30，永磁体剩磁Br为1.08T，永磁体矫顽力Hc为-796000A/m，空气磁导率μ0为4π×10-7H/m，（BH）max取223kJ/m3，环形永磁体内径R1为14.5mm，环形永磁体外径R2为20.5mm，环形永磁铁长度L1为4mm，柱形永磁体半径r为9mm，柱形永磁体和环形永磁体间的轴向气隙z=0.5mm、取长度 L2为 8mm、10mm、12mm、14mm、16mm 的柱形永磁铁进行实验，测量径向偏移量为e=2mm时的径向磁力值。如上条件的实验结果与相同条件下的仿真结果对比呈现，如图9所示。由图9可以看出，在上述实验条件下，永磁弹簧的径向磁力随柱形永磁体长度的增加而增加，实验测量与仿真结果的平均误差为0.0989N以内，最大误差0.154N。基本能够满足工程要求。

3.2.4 永磁体直径参数的对比分析

实验中，永磁体材料NdFeB N30，永磁体剩磁Br为1.08T，永磁体矫顽力 Hc为（-796000）A/m，空气磁导率 μ0为 4π×10-7H/m，（BH）max取223kJ/m3，环形永磁体内径R1为14.5mm，环形永磁体外径R2为20.5mm，环形永磁铁长度L1为4mm，柱形永磁铁长度L2为10mm，柱形永磁体和环形永磁体间的轴向气隙z=0.5mm、取半径r为6mm、7mm、8mm、9mm、10mm的柱形永磁铁进行实验，测量径向偏移量为e=2mm时的径向磁力值。如上条件的实验结果与相同条件下的仿真结果对比，如图10所示。由图10可以看出，在上述实验条件下，永磁弹簧的径向磁力随柱形永磁体半径的增加而增加，当环形永磁体与柱形永磁体半径偏差较大，径向位移不大的情况下，径向回复斥力并不明显。

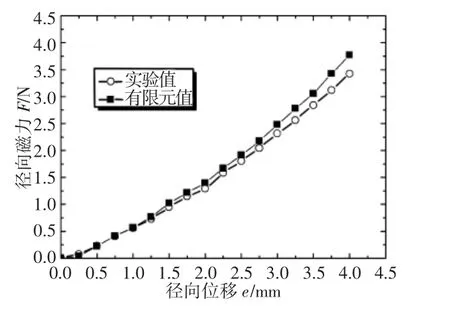
图8 变径向偏移量的实验与仿真对比图Fig.8 The Comparison of Changing Radial Displacement Between Experiment and Simulation

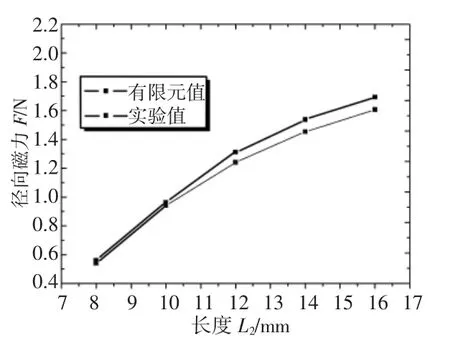
图9 变永磁体长度实验与仿真对比图Fig.9 The Comparison of Changing Permanent Length Between Experiment and Simulation

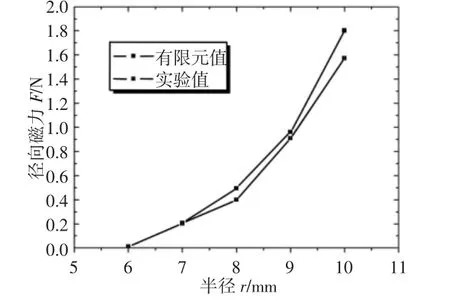
图10 变永磁体半径实验与仿真对比图Fig.10 The Comparison of Changing Permanent Radius Between Experiment and Simulation

4 结论

利用ANSOFT软件，对3自由度等刚度永磁弹簧的尺寸参数特性进行了有限元分析，分析了不同尺寸参数对永磁弹簧径向力学特性的影响。并将有限元分析结果与实验测量结果进行了比较，结果表明采用的有限元分析能够满足工程要求。在此基础上，总结出随着环形永磁体平均半径的增加，弹簧径向磁力减小。随着柱形永磁体的半径和轴向长度、环形永磁体的轴向长度的增加，弹簧径向磁力增加。随着环形永磁体和柱形永磁体间的竖直方向气隙长度的增加，弹簧径向磁力呈抛物线趋势变化的规律。但当环形永磁体与柱形永磁体半径偏差较大，径向位移不大的情况下，径向回复斥力并不明显。该研究结果对提高3自由度永磁弹簧的性能有一定的实际意义和应用价值。