减振器螺旋弹簧组串并联刚度计算与分析
2018-09-17冯治国李长虹余世捷
可 帅,冯治国,李长虹,余世捷
(贵州大学 机械工程学院,贵州 贵阳 550025)
1 引言
汽车行驶的过程中,减振器中的弹簧起着缓冲和减震的作用,由于路况不同,弹簧要不断承受高频往复的运动,因此弹簧减振能力和质量的好坏,直接影响着车辆的平稳性和安全性。在弹簧减振器中,把不同性能的弹簧按照一定的方式组成新的弹簧组系统,往往比单只弹簧的使用更加普遍。弹簧组的使用提高了传统的单只长弹簧的侧向稳定性。为改善货车小载荷下的运行品质,提高对扭曲线路的适应能力,货车转向架弹簧悬挂装置中两级刚度弹簧组早在上世纪50年代就在前苏联X-2型货车转向架上得到应用。在国外一些国家的货车转向架上,两级刚度弹簧组都程度不同地得到了应用。
在解决管道热力学膨胀的问题中,国外科研人员采用多级弹簧串联使用,由多个弹簧来共同分担热位移的影响。使用具有不同弹簧刚度的并联弹簧组,不仅能保证减振器具有高的支撑刚度和较低的运动刚度。同时很好解决了在传统隔振系统中存在的稳定与隔振问题[1]。弹簧组的使用在目前的减振设备中用的越来越普遍。弹簧组是指由几个弹簧按照新的组合方式重新形成的一个全新系统,它的组合方式主要有并联和串联[2]。串联弹簧组得出的刚度比期中任何一个弹簧刚度都小,并联弹簧组的使用往往是为了解决单只弹簧刚度不足的问题。根据实际的需要,有时候也会把串联弹簧组和并联弹簧组一起作为减振系统来使用。目前,弹簧刚度的计算公式是根据材料力学,和第四强度理论并通过实验不断修正的方法[3]。但是实验的设计阶段没有实验数据只能以其他的相近代替,如果没有生产的实际经验,很难设计和制造出来高精密的弹簧组,特别是随着生产力,产品要求的不断提高,一些传统的设计经验不再适用[4]。
因此很有必要用一种新的能快速准确计算不同弹簧组刚度的方法。用ANSYS软件分别对串联、并联弹簧组的刚度计算,并利用matlab矩阵强大的拟合画图能力得到弹簧组的刚度曲线,并与传统的理论计算作对比得到一种新的弹簧组计算方法。
2 弹簧组三维实体模型的建立
建立弹簧的三维模型,使用弹簧的常用材料铜合金作为来分析计算,铜合金材料的密度为8300kg/m3,剪切模量为4.1045E+10Pa。实际中弹簧连接处的结构比较复杂,为了简化设计中弹簧组连接处的不同情况,用方块立方体代替中间的接触件,同时为了减少其对弹簧整体刚度的影响采用剪切模量达到7.6923E+10Pa的结构钢,更高的剪切模量会在一定程度上减少误差,结构钢密度为7850kg/m3,方块立方体的长宽高为:25mm、25mm、5mm。
具体的几何参数:

表1 弹簧几何尺寸参数Tab.1 Spring Geometry Parameters
根据以上参数的设定,通过三维建模软件UG建立串联弹簧组的实体模型,并保存为X_T格式。
为了减小减振器的弹簧的刚度和侧向稳定性问题,串联弹簧组在减振器的使用中更加普遍,采用一种独立阻尼双弹簧串联减振调压装置中的串联弹簧组简化模型,本装置配合弹簧组的使用,提高了压力阀的动态稳定性,工作更加平稳,动态特性更好[5]。
为了提高弹簧的性能,常采用两个或多个直径不同的弹簧同心安装,形成组合弹簧,此并列式组合弹簧为高速车辆一系轴箱螺旋弹簧组简化模型。此类弹簧可承受较大载荷,为了避免支撑面的过大扭转和弹簧间相互干扰,弹簧的旋向分别有左旋和右旋,交替安装组合弹簧的等效刚度为两根弹簧刚度之和。这种旋向不同的并联弹簧组因具有优良的性能,广泛应用于各种弹簧减振器中[6]。
3 串、并联弹簧组的理论刚度
普通圆柱螺旋弹簧垂直刚度公式的推导可以利用能量方程来推导,使弹簧受到外力所的功全部等于弹簧弹性势能的增长量,经过一定的转换就可以得出来弹簧的刚度公式。设作用在弹簧上的作用力为F,同时弹簧的变形量为λ,则可以计算出来该外力做的功[7]:

弹簧的弹性势能为:
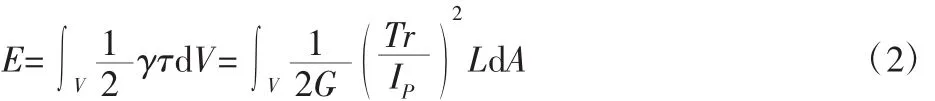
弹簧的圈数为n,所以弹簧的长度L=πDn,进一步对以上(2)式进行积分化简:

根据能量守恒定律,外力所做的功等于储存在弹簧内的弹性势能,因此可知:

化简可得螺旋弹簧的刚度:

式中:G—材料的剪切模量;d—弹簧丝的直径;n—有效的圈数;
D—弹簧的中径。
弹簧组往往是由几个特殊要求大小的弹簧重新串联或者并联组成的新系统,设串联系统的刚度为K串,并联系数的关系为K并。下面推导K串,K并与各个弹簧K1,K2的关系。串联时他们受力相等,设为F,设各自的伸长量分别为Δx1和Δx2,弹簧总的伸长量为Δx。则根据胡克定律F=KΔx表达式计算:

上式即为串联弹簧组的刚度计算公式。
当并联时,弹簧组受到的总拉力为两个弹簧拉力之和,根据关系可得:

整理可得:K并=K1+K1(10)
上式即为并联弹簧组的刚度计算公式。
将材料参数和弹簧的几何尺寸带入(5)分别计算出大弹簧和小弹簧的刚度:

带入到式(7)、式(10)分别得出:

4 有限元分析
4.1 弹簧组的有限元分析模型的建立
ANSYS有限元软件是一个多用途的有限元法计算机设计程序,可以用来求解结构、流体、电力、电磁场及碰撞等问题。用来求解外载荷引起的位移、应力和力。其中静力分析很适合求解惯性和阻尼对结构的影响并不显著的问题。ANSYS程序中的静力分析不仅可以进行线性分析,而且也可以进行非线性分析,如塑性、蠕变、膨胀、大变形、大应变及接触分析。
将T_X格式的UG三维实体模型导入到有限元分析的软件ANSYS中,有限元计算分析的最根本目的是还原实际的数学行为特征,把实体的物理模型最终还原为精确的数学模型。
通过ANSYS的自由网格划分可以快速的得到平面图形上的三角形四边形网格,和体上的四面体网格。其内部的智能控制技术(SMARTSIZE命令)不仅可以设置网格的大小(AESIZE、LESIZE、KESIZE、ESIZE等系列命令),而且还能控制网格的疏密程度。以及选择分网算法等(MOPT命令)。对于复杂几何模型而言,这种分网方法省时省力。考虑到弹簧组机构的复杂情况采用自由网格划分节[8]。
减振器中的串、并联弹簧组在汽车的行驶过程中,承受高频往复的运动,在受到载荷后产生较大的弹性形变,吸收并储存能量,起到缓冲和减振的作用。弹簧组在压缩变形的过程中,弹簧截面收到的载荷主要有剪应力,压应力、扭矩等。加上弹簧丝存在一定的曲率,实际变形及受力相当复杂。基于此文中对串、并联弹簧组进行垂直刚度的有限元分析是对弹簧组施加垂向力,而对扭转减振器弹簧组的扭转刚度的有限元分析通过添加力偶矩来实现。对弹簧组进行主要载荷的添加而忽略次要受力因素的影响。
串联弹簧组的节点数目为:49341单元总数为15336。并联弹簧组的节点数目为:34090单元总数为:12202。

图1 串联弹簧组网格划分结果Fig.1 Grid Series Spring Group

图2 并联弹簧组网格划分结果Fig.2 Parallel Meshing Spring Group
4.2 对串联弹簧组的压力与变形的分析
利用有限元的静力学分析模块,首先固定好大弹簧的受力点,然后对连接小弹簧的结构钢施加不同的法向力,来观察弹簧的位移改变大小,如图3所示。

图3 串联弹簧组的有限元分析变形图Fig.3 Series Spring Set of Finite Element Analysis of Deformation Figure
对弹簧组施加不同的法向力得到不同的法向位移,将这些数据经过一次拟合后得到一条,法向力与法向距离之间的线,根据胡克定律F=KΔx可知这条线的斜率就是该变形下弹簧组的总刚度[9]。

表2 所施加的压力与位移改变的数据Tab.2 Pressure and Displacement Change of Data
通过有限元分析得到法向力和法向位移的关系从而出串联弹簧组法向力和位移的图,用Matlab强大的作图功能,把仿真得出的数据点拟合出来一条直线[10],这条直线的斜率就是串联弹簧组的刚度(7.8108×103)n/m。

图4 串联弹簧组刚度有限元与理论结果曲线Fig.4 Series Spring Set Finite Element Stiffness Curve with Theoretical Results

4.3 对并联弹簧组的压力与变形的分析

图5 并联弹簧组有限元分析变形图Fig.5 Parallel Springs of Finite Element Analysis of the Deformation
对并联的弹簧组施加不同的法向力,并计算出不同法向力作用下法向位移的大小。得出并联弹簧组法向力和位移的图,可以看出来是一条直线,这条直线的斜率就是并联弹簧组的刚度(4.5301×104)n/m。

表3 所施加压力与位移改变数据Tab.3 The Pressure and Displacement Change the Data

图6 并联弹簧组刚度有限元与理论结果曲线Fig.6 Parallel Springs of the Finite Element Stiffness Curve with Theoretical Results
从上面也可以发现线性弹簧所组成的串并联弹簧组的刚度也具有线性的特征。
5 扭转减振器刚度分析
5.1 扭转减振器刚度的理论计算
扭转减振器具主要有线性和非线性特性两种。扭转减振器的组成主要是弹簧等弹性元件。弹性元件的主要作用是控制动力传动系总成怠速时离合器与变速器轴系的扭振,消减变速器怠速噪声和主减速器与变速器的扭振与噪声缓和非稳定工况下传动系的扭转冲击载荷和改善离合器的接合平顺性。
通过降低传动系的扭转刚度,以此来降低减振系统的固有频率,改变系统的固有振型,使之尽可能避开由发动机转矩主谐量激励引起的共振。为了避免引起系统的共振,要合理选择减振器的扭转刚度Kφ,使共振现象不发生在发动机常用工作转速范围内Kφ决定于减振弹簧的线刚度及其结构布置尺寸。

式中:Zj—减振器中弹簧的个数;R0—减振器中弹簧布置半径;K—每个减振弹簧的线刚度。
扭转减振器的刚度主要有并联弹簧组刚度、弹簧组数目、弹簧组布置半径决定。由于单级扭转减震器中使用最广泛的是并联弹簧组的弹性元件,因此主要对上述高速车辆所使用的具有并联弹簧组的减震器进行计算,该减振器所用弹簧组为八个,带入并联弹簧组的刚度K并、弹簧数目Zj半径R0可以得出减振器的扭转角刚度,公式中K并,Zj,R0均为常数,所得出最后扭转角刚度随着载荷的增加而增加同时呈现出线性特征。
5.2 扭转减振器刚度的有限元分析
装有并联弹簧组的扭转减振器在工作的时候,弹簧组会受到垂直于布置半径的力矩的作用,在进行有限元分析的时候可以在弹簧组的顶端添加一个力偶矩,改变力偶矩的大小可以得出弹簧组在水平和竖直方向上的位移发生改变,经过一定的换算关系便可以得出力偶矩与弹簧组弯曲角度的关系,因此把上述并联弹簧组的模型导入分析软件根据有限元得出的数据点平均值为1930.5N/m/rad,而理论计算得出Kφ=2038N/m/rad,误差范围在6%左右,仿真结果与理论计算结果比较契合。对于单级减振器的扭转刚度在一定范围内仍然具一定的线性关系。
从图4、图6可以明显看出弹簧组的法向力与法向位移呈直线关系分布。串、并联弹簧组与扭转减振器扭转刚度的理论计算值和有限元的分析结果误差分别在6%、7%、6%误差在承受范围内,产生误差的主要原因在于弹簧在载荷作用下,由于上下移动,垂向载荷的作用位置随之发生变化,在弹簧两端切口的影响下,弹簧的受力状态发生变化,垂向刚度随载荷的变化而变化比较明显。同时在有限元分析载荷添加时忽略了所求刚度方向之外其他方向载荷的影响。总体来看线性弹簧组成的串并联弹簧组的刚度仍具有线性特征。
6 结束语
基于胡克定律对串、并联弹簧组刚度进行了数学理论计算,建立弹簧组合理的有限元模型,利用Matlab数据处理平台分别拟合出弹簧组理论计算和有限元分析的刚度曲线,得出弹簧组线性刚度和扭转刚度的平均误差在6%左右,通过以上分析数据发现,理论计算结果与仿真分析结果比较接近,验证了有限元模型的合理性和正确性。同时有限元分析能更加快速直观的得到弹簧的具体受力情况,因此可缩短更复杂弹簧组刚度计算周期,对于工程实际有一定的指导意义。
