基于EVIEWS的各省市高考升学率的影响因素分析

范 娟 巴桑卓玛

(西藏大学理学院 西藏 拉萨 850000)

一、引言

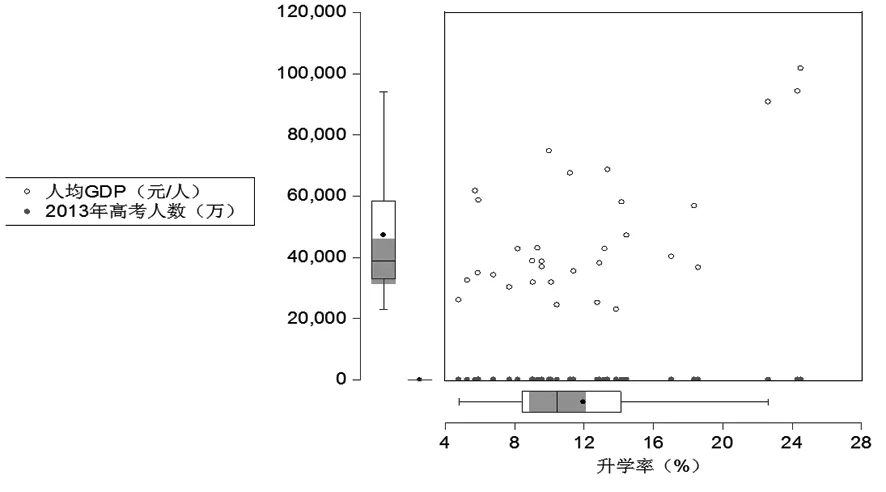
在升学率压力下,这一场域中处于不同位置的组织采取不同的行动策略。在学校组织内部,不同学校采取的共同策略是围绕考试内容和分值对知识、教师和学生不断归类并进行应试规训,由此导致教师和学生的地位不断分化,形成若干身份群体。本文将通过实证调研,揭示为高考升学率与各省市的人均GDP、报考人数的关系,以及东中西部地区对升学率的影响。

二、模型的建立

研究2013年全国31个省市的人均GDP、高考报考人数以及该省市是否为中部、西部和东部地区这三个因素对该省市一本升学率的影响。样本区间为2013年的31个省市,被解释变量Y为2013年31个省市的一本升学率,解释变量为各省市人均GDP为X1、各省市高考报考人数X2、该省市是否为中部、西部和东部地区(虚拟变量D1、D2)。因此,我们需要建立多元线性回归模型。即Y＝c＋B1X1＋B2X2＋B3D1＋B4D2＋u,显著性水平为0.05。

式中:μ:随机扰动项

其中最小二乘法对模型中随机扰动项μ的要求是μ符合正态分布.在判断μ是否符合正态分布时,我们无法直接观测到μ,因此需要通过对残差μ进行分析来检验μ。

(一)JB检验

JB检验是通过JB统计量进行正态性检验的方法。JB统计量全称为Jarque－Bera统计量,是根据残差ei对大样本是否符合正态分布进行检验的数学方法。

式中:n:样本容量当大样本为正态分布时,JB检验量服从如下卡方分布:

式中:asy:渐进的

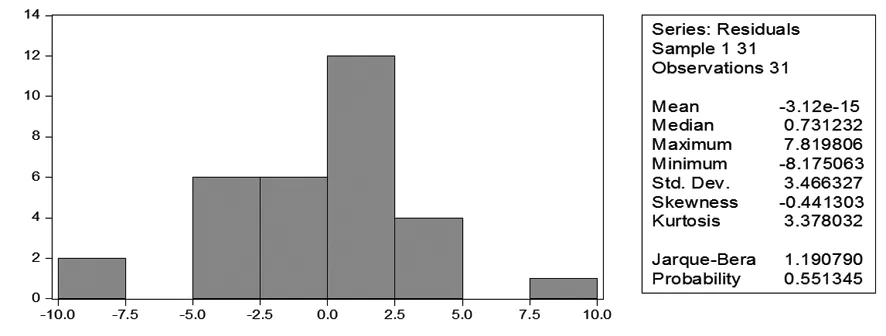
综上可知,如果被测样本符合正态分布,则S＝0.091134,K＝1.6,JB＝0;若被测样本不符合正态分布,则JB的值将不断增大.给定显著性水平α＝0.05,查表可知χ2(2) ＝0.978.由表2计算可知,S＝0.04372,K＝0.167,JB＝1.190790＜5.99147,所以该数据符正态分布,可以用最小二乘法进行计算。Jarque－Bera项的伴随概率Probability为0.551345＞0.05,表明随机扰动项是正态的。

(二)一元线性回归

经过上述分析,可以用建立一元回归方程的形式表示Y与X间的关系,用EViews回归所得结果如表3:

所得结果为:Y＝8.477559＋0.000167X1－0.09959X2－2.236101D1－2.315184D2 t＝ (3.666)(3.636)(－2.504)(－1.198)(－1.044)

R2＝0.585 D.W＝1.073 s.e＝3.723 F＝9.161 T＝31

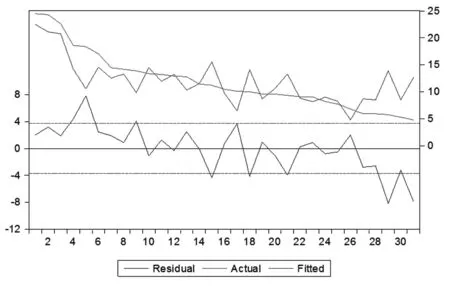
通过结果可以看出:

(1)R－squared很小,说明自变量与因变量之间拟合得不是很好。

(2)虚拟变量D1 D2的t值较小

(3)回归结果的D统计量的值1.073284可以初步断定是存在一阶自相关的

四、结论与建议

本研究以我国各省区高考一本升学率作为因变量,以人均GDP作为自变量代表各省区经济发展水准,并且也将报考人数作为自变量之一,以省区为单位进行分析经济发展水准对高中升学率的影响。从回归结果来看,一本升学率受各省市人均GDP的影响较大,而各省市高考报考人数的影响并不大,这一结果还是较符合基本现实状况的;D1不显著D2显著说明一本升学率在中西部地区地区无差异,在东部和中西部地区是有差异的,在我国高等教育大众化与经济发展的进程中,研究经济水准对高等教育大众化的影响具有实践意义。