焦半径、焦点弦公式在高考中的应用

☉湖北省武汉市武昌实验中学 李乐恒

众所周知，抛物线上任意一点与焦点之间的所连线段的长度，叫做焦半径；过抛物线焦点的直线被抛物线截得的线段叫做焦点弦.焦半径、焦点弦是抛物线中的重要几何性质，因其能与直线的倾斜角、向量（定比分点）、三角形面积等知识交汇，故备受命题人青睐，而成为近年来高考试题、自主招生试题中的一个热点问题，作为客观题中的压轴题，甚至解答题进行考查，以测试考生数学知识和思想方法的掌握和运用.

一、考题重现

下面列举5个近年来焦半径、焦点弦在新课标试卷中考查过的试题：

1.（2017新课标Ⅰ，理10）已知F为抛物线C：y2=4x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A，B两点，直线l2与C交于D，E两点，则|AB|+|DE|的最小值为（ ）.

A.16 B.14 C.12 D.10

2.（2014新课标Ⅱ，理10）设F为抛物线C：y2=3x的焦点，过F且倾斜角为30°的直线交C于A，B两点，O为坐标原点，则△OAB的面积为（ ）.

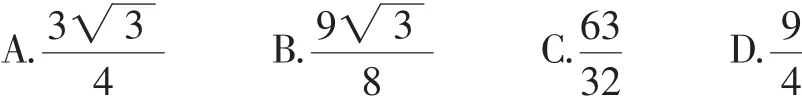
3.（2014新课标Ⅱ，文10）设F为抛物线C：y2=3x的焦点，过F且倾斜角为30°的直线交C于A，B两点，则|AB|=（ ）.

4.（2013新课标Ⅱ，文10）设抛物线C：y2=4x的焦点为F，直线l过F且与C交于A，B两点.若|AF|=3|BF|，则l的方程为（ ）.

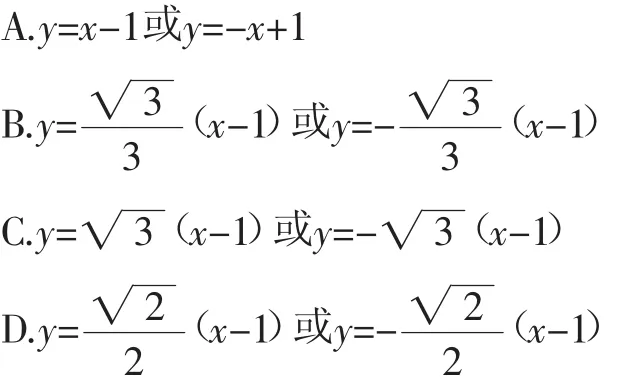
5.（2016新课标Ⅲ，文20（1）理20（1））已知抛物线C：y2=2x的焦点为F，平行于x轴的两条直线分别交C于A，B两点，交C的准线于P，Q两点.若F在线段AB上，R是PQ的中点，证明AR∥FQ.

二、教材出处

上述问题涉及抛物线的焦点弦、焦半径的长度计算.在教材中追根溯源，其出处是：普通高中课程标准试验教课书《数学选修2-1A版》（人民教育出版社2007年2月第2版）（以下简称课本）.

（1）课本第69页例4：斜率为1的直线l经过抛物线y2=4x的焦点F，且与抛物线交于A，B两点，求线段AB的长.

（2）课本第70页例5：过抛物线焦点F的直线与抛物线交于A，B两点，通过点A和抛物线顶点的直线交抛物线的准线于点D，求证：直线DB平行于抛物线的对称轴.

三、题根延伸

下面以课本中这两道抛物线焦点弦、焦半径的“题根”，延伸出如下6个问题或结论：

设AB是过抛物线y2=2px（p>0）焦点F的一条弦，A（x1，y1），B（x2，y2），直线AB的倾斜角为θ.

（1）抛物线中的定值问题：y1y2=______，x1x2=______.

（2）抛物线焦半径的长度：|AF|=_____，|BF|=______.

（3）抛物线焦点弦的长度：|AB|=______.

（4）焦点弦中最短的弦（通径）的长度=______.

（6）△OAB的面积=______.

（2）过A作AA1⊥l于A1（l为准线），

则|AF|=|AA1|=p+|AF|cosθ，

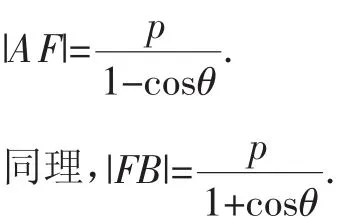
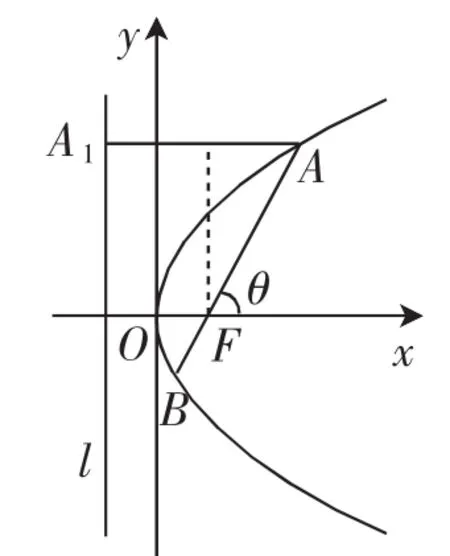
图1

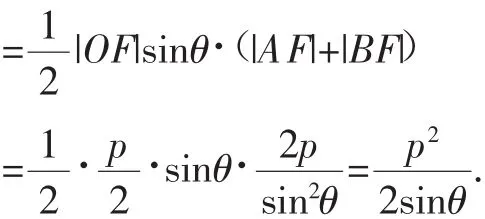
注：当焦点在y轴上时，将cosθ换为sinθ，sinθ换为cosθ.

四、考题解答

五、解答总结

从以上各题可以看出，解决这类问题的常规解法，是按照解析几何问题求解的“三部曲”，联立直线和曲线方程，消元得到关于x或y的一元二次方程，用韦达定理得到焦点坐标的关系式，最后将目标转化表示，运算量往往较大，若运用焦半径公式的倾斜角形式，可以简化运算，直达结论，起到事半功倍的效果.H