2018年高考命题创新的四个视角*

2018-09-15四川内江师范学院数学与信息科学学院刘成龙

中学数学杂志 2018年17期

☉四川内江师范学院数学与信息科学学院胡琳刘成龙

创新作为第一动力，高考数学命题应始终坚持这一导向.高校要选拔具有创新潜质的人才，高考数学必须重视对学生创新意识的考查.研究近年高考试题，不难发现创新成为了新的热点和亮点.高考命题创新体现在四个方面：命题理念创新、试题题型创新、试题背景创新和试题解法创新.其中，理念创新是命题创新的灵魂，题型创新是命题创新的抓手，背景创新是命题创新的载体、解法创新是命题创新的落脚点，这四个方面相互促进、相互渗透，构成了一个完整的命题创新系统（如图1）.本文以2018年高考试题为例，分析高考命题创新的四种视角以及创新视角下的几种创新型试题.

图1

视角一、命题理念创新

命题理念引领命题工作的开展.一直以来，高考命题理念处于不断的调整中，比如从“双基”立意发展到能力立意，再发展到素质立意等等.十九大明确提出“落实立德树人根本任务”.在此背景下，2018年高考命题将“立德树人、服务选才、引导教学”作为高考的核心功能.这是对命题理念的创新.基于此，命制了立德树人型、素养立意型试题.

1.立德树人型

“课标”指出：数学教育承载着落实立德树人根本任务.高中课程内容要落实习近平新时代中国特色社会主义思想，有机融入社会主义核心价值观，中华优秀传统文化、革命文化和社会主义先进文化教育内容，充实丰富培养学生社会责任感、创新精神、实践能力相关内容［1］.2018年高考命题坚持立德树人的基本导向，命制了一系列立德树人型试题，意在通过德育渗透，培养学生良好的道德品质.

例1（2018年全国Ⅲ卷3题）中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫棒头，凹进部分叫卯眼，图2中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（）.

图2

评析：榫卯（sǔn mǎo），是中国古代传统的一种木匠工艺，指在两个构件上采用木头凹凸拼接的形式，凸出来的部分称为“榫”，凹进去的部分叫做“卯”，榫卯相契合，从而使木头与木头完美衔接.榫卯是极为精巧的发明，这种构件连接方式，使得中国传统的木结构成为超越了当代建筑排架、框架或者钢架的特殊柔性结构体，不但可以承受较大的荷载，而且允许产生一定的变形，在地震荷载下通过变形抵消一定的地震能量，减小结构的地震响应.本例以榫卯为载体，着重介绍我国工匠们的精湛技艺、感悟古人的伟大智慧，这凸显了我国古建筑技艺的世界领先地位.一方面，可以让学生了解传统文化，便于传承传统技艺，增强文化自信，培养学生的爱国主义情怀；另一方面，通过感受古人的价值观和世界观，增强学生社会责任感，育人于无声无息之中.

2.素养立意型

素养指数学学科核心素养.数学学科核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，是在数学学习和应用的过程中逐步形成和发展的.数学学科核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析［1］.2018年高考命题将考查核心素养作为基本理念，这是对“双基”立意、能力立意、素质立意的深化.

例2（2018年全国Ⅲ卷理科第19题）如图3，边长为2的正方形ABCD所在的平面与半圆弧C（D所在平面垂直，M是C（D上异于C，D的点.

（Ⅰ）证明：平面AMD⊥平面BMC；

（Ⅱ）当三棱锥M-ABC体积最大时，求平面MAB与平面MCD所成二面角的正弦值.

解：（Ⅰ）证明略.

（Ⅱ）当三棱锥M-ABC体积最大时，M位于C（D的中点.将原图补成如图3的三棱柱，显然平面MAB与平面MCD所成二面角为∠APD，于是sin故平面MAB与平面MCD所成二面角的正弦值为

图3

评注：本例着重考查学生直观想象素养.直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养.主要包括：借助空间形式认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题；构建数学问题的直观模型，探索解决问题的思路.第（Ⅱ）问的解答方法有多种，比如：向量法、几何法（定义法）等等，但众多方法中补形法真正揭示了问题的本质，体现了几何直观的重要魅力.我们认为命制本例的意图是增强运用几何直观和空间想象思考问题的意识，形成数学直观，在具体的情境中感悟事物的本质.

视角二、试题题型创新

试题题型创新是理念创新的直接体现.高考命题在试题题型上的创新步伐一直没有停止.《2018年普通高等学校招生全国统一考试大纲：理科》（下文简称《考试大纲》）指出：“在考试中要有研究型、探索型、开放型等类型的试题［2］.”研究型、探索型、开放型试题正是高考命题开发的创新型试题.这些类型试题对拓宽学生思维模式、丰富学生认知结构有益.基于此，2018年高考中呈现了一些题型创新试题.

1.结论开放型

按题目中条件或结论等成分确定与否，可将数学题分为封闭题和开放题两类.凡是具有完备的条件和固定的答案的题目称为封闭题，凡是答案不固定或者条件可以变化的题目称为开放题［3］.其中，条件固定，答案不固定的题目称为结论开放型试题.结论开放型试题将思维的空间留给了学生，将话语权留给了学生，有利于培养学生自主探究的学习方式.

例3（2018年北京卷理科13题）能说明“若f（x）>f（0）对任意的x∈（0，2］都成立，则f（x）在［0，2］上是增函数”为假命题的一个函数是______.

评析：本例结论不唯一，是典型的结论开放型试题.学生解答本例可能出现无穷多个答案，这充分暴露了学生的思维，展示了学生的自主权.尽管开放性试题给阅卷工作带来困难，但其体现的是思维的多元化，这也正是命题者命制开放性试题的初衷.

2.阅读理解型

阅读属于信息输入加工形式，是人类汲取知识、认识世界的一个重要方式.而数学阅读是指学生根据已有的知识和经验，通过阅读数学材料（数学公式、方法、图形、符号、文字等）汲取信息，建构数学意义和方法的心理和智力过程［4］.数学阅读过程是一个完整的心理活动过程，包含语言符号的感知和认读，新概念的同化和顺应，阅读材料的理解和记忆等各种心理活动因素.同时它也是一个不断假设、证明、想象、推理的积极能动的认知过程.从心理学角度分析，数学理解的本质是学习者在头脑中形成关于这个知识的内部网络，即建立了该知识的图式［5］.阅读理解型试题是指以阅读材料形式呈现的试题.阅读材料往往介绍一个新定义、一种新规则、一种新运算、一种新关系，这些新的信息提供给学生一个新的问题情境，学生需要经历现场筛选—加工—内化—运用等过程，显然该试题是对传统试题的一种命题创新.

例4（2018年北京卷理科20题）设n为正整数，集合A={α|α=（t1，t2，…，tn），tk∈{0，1}，k=1，2，…，n}.对于集合A中的任意元素α=（x1，x2，…，xn）和β=（y1，y2，…，yn），记M（α，β）=［（x+y-|x-y|）+（x+y-|x-y|）+…+（x+11112222nyn-|xn-yn）|］.

（Ⅰ）当n=3时，若α=（1，1，0），β=（0，1，1），求M（α，α）和M（α，β）的值.

（Ⅱ）当n=4时，设B是A的子集，且满足：对于B中的任意元素α，β，当α，β相同时，M（α，β）是奇数；当α，β不同时，M（α，β）是偶数.求集合B中元素个数的最大值.

（Ⅲ）给定不小于2的n，设B是A的子集，且满足：对于B中的任意两个不同的元素α，β，M（α，β）=0.写出一个集合B，使其元素个数最多，并说明理由.

评析：本例是典型的阅读理解型试题.本例呈现三新：情境新、规则新、问题新，这需要学生调整思维方式，快速进入新的问题系统.例中有三多：数学符号多、文字多、问题多，这需要学生具有较强的阅读能力、迁移能力.解答时，学生需要经历信息筛选→信息加工→概念内化→概念应用，整个过程为：通过阅读认识集合A中代表元素的特征（n维空间中的点），厘清集合A中任意两元素α，β做运算的规则M（α，β），并深刻认识在此规则下M（α，β）是一个数，然后运用规则解答问题.解答过程中包含新定义的认识、理解、运用，着重考查学生的阅读理解能力和信息加工能力.

视角三、命题背景创新

命题背景指命题时所选取的素材.试题背景引领着试题编拟的方向，凸显试题的立意.2018年高考命题背景有以下特点：有浓浓的高数味道，密切联系时代特征，学科间相互交融，充满文化气息等等.由此，衍生出了命题取材创新的两类题型：高等背景型、学科交汇型.

1.高等背景型

高等背景指命题时选取素材中含有的高等数学知识、模型、问题、思想和方法，这些知识、方法、问题、思想和方法称为高等数学背景.高等数学背景命题具有积极作用：强化中学数学与高数知识间的衔接，展示新颖的数学背景，丰富试题的内涵，拓宽试题解法，考查学生创新能力和创新意识［6］.2018年以高等数学为背景的试题呈现了高度的创新性，很好地考查了学生的创造力与发展力，有效地甄别了学生的潜质.

例5（2018年全国Ⅲ卷理科21题）已知函数f（x）=（2+x+ax2）ln（1+x）-2x.

（Ⅰ）略；

（Ⅱ）若x=0是f（x）的极大值点，求a.

评析：本例含有深刻的高等数学背景，比如：洛必达法则、麦克劳林公式、帕德逼近等等.下面重点介绍帕德逼近背景下试题的命制：

函数f（x）=（2+x+ax2）ln（1+x）-2x中ln（x+1）系数2+x+ax2是怎么设置出来的呢？答案a=是怎么设置出来的呢？这些均源于帕德逼近，表1是函数（fx）=ln（x+1）在（0，0）处到（3，3）阶的帕德逼近表.

表1

本例设计精巧、构思巧妙，对学生创新能力要求极高，这为2019年命制创新试题作出了示范.

2.学科交汇型

数学源于哲学.因此，数学与其他学科有着千丝万缕的联系.2018年高考命题注重数学与其他学科交汇考查，这对认识数学的基础地位，拓宽数学学科研究领域、完善认知结构有积极的意义.

例6（2018年北京卷理科4题）“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展作出了重要贡献.十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于若第一个单音的频率为f，则第八个单音的频率为（）.

评析：本例选材于音乐学科中的十二平均律.十二平均律，亦称“十二等程律”.世界上通用的把一组音（八度）分成十二个半音音程的律制，各相邻两律之间的振动数之比完全相等.明朝中叶，皇族世子朱载堉发明以珠算开方的办法，求得律制上的等比数列，具体说来就是：用发音体的长度计算音高，假定黄钟正律为1尺，求出低八度的音高弦长为2尺，然后将2开12次方得频率公比数1.059 463 094，该公比自乘12次即得十二律中各律音高，且黄钟正好还原.用这种方法第一次解决了十二律自由旋宫转调的千古难题.本例以“十二平均律”为载体，考查了等比数列的相关知识，通过“冰冷”的数学美与极具韵味的音乐完美碰撞，产生了独特的意蕴美.

视角四、解答方法创新

解答方法创新是命题创新的落脚点.解题涉及方法的选取，好的方法令人赏心悦目，充分暴露思维的灵活性和策略的创造性.2018年高考命题以“多一点想，少一点算”为出发点，命制了一些解答方法创新的试题.

1.思想引领型

例7（2018天津卷理科8题）如图4，在平面四边形中，AB⊥BC，AD ⊥CD，∠BAD=120°，AB=AD=1，若点E为边CD上的动点，则—的最小值为（）.

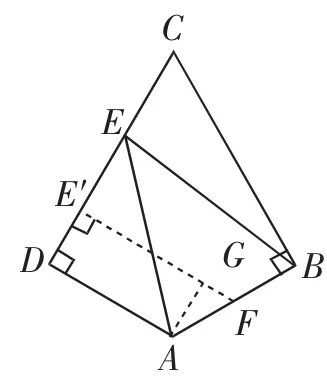
图4

评析：数学思想是对数学知识的本质认识，是对数学规律的理性认识，是从某些具体的数学内容和对数学的认识过程中提炼上升的数学观点［7］.本例考查了模型思想，所谓模型是一种结构，这种结构是通过对原型的形式化或模拟与抽象得到的.数学模型就是研究者依据研究目的，将所研究的客观事物的过程和现象的主要特征、主要关系，采用形式化的数学语言，概括或近似地表达出来的一种结构.本例解答中运用了向量恒等式模型，优化了问题解决，这充分展示了思想的引领作用.