如何找准解题思路切入点——以一道解几模拟题的多解剖析为例

☉江苏省常熟市中学 吴晓鹏

问题是数学的生命，数学解题思路则是生命运行的轨迹.如何运用不同的思维方法，找准问题适合的切入角度，呈现出丰富多彩的解题思路，让学生体会到因不同的切入点而带来的策略、技巧、效果、效率的变化，提升学生对知识体系的认识程度和关联能力，是我们在教学中亟待解决的问题，也是数学核心素养的要求之一.本文就以2018届江苏省苏锡常镇一模第13题为例，来谈一谈如何找准解题思路的切入点.

【问题】（2018届江苏省苏锡常镇一模·13）已知直线l：x-y+2=0与x轴交于点A，点P在直线l上，圆C：（x-2）2+y2=2上有且仅有一个点B满足AB⊥BP，则点P的横坐标的取值集合为______.

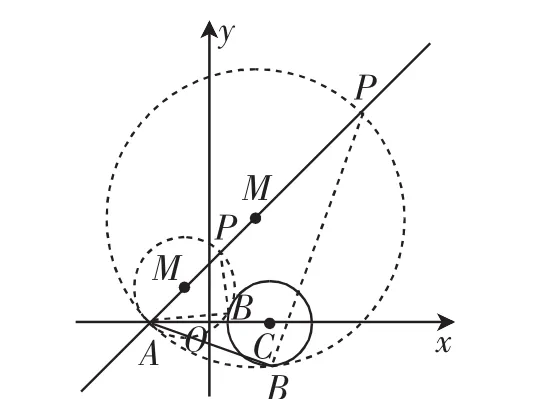
图1

分析：本题巧妙借助直线与圆之间的特殊关系，综合直线的方程、圆的方程、垂直关系等相关的知识，以静观动、以动求静，来确定对应点的坐标问题.而采用不同的切入点，对应着不同的解题方法.根据对应的图像可知，满足条件的P有两个对应的点，其所确定的以AP为直径的圆与圆C的关系分别是外切与内切.

切入点1（紧扣定义）：理解、掌握定义，并能灵活使用定义，是解题必备的技能，也是迅速找到切入点的重要手段.

思路分析1（圆与圆的位置关系法1）：先由A，P两定点及AB⊥BP可知B点轨迹是圆作为切入点，从而确定B为两圆唯一的公共点，利用两圆相切来解题.

解法1：设点P的坐标为P（t，t+2）.

因为圆C上有且仅有一个点B满足AB⊥BP，所以以AP为直径的圆和圆C相切，

而以AP为直径的圆的方程为

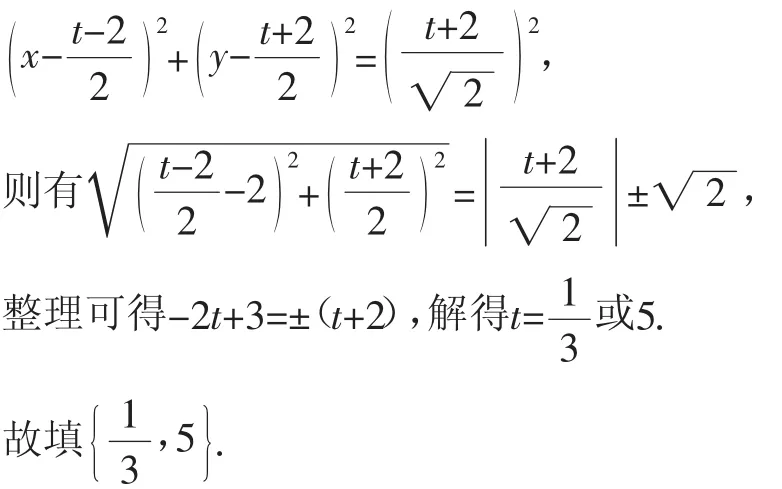
思路分析2（圆与圆的位置关系法2）：在设点运算这一环节，采用P（t，t+2）运算较为复杂，考虑到圆的定义中M（M为AP中点）为圆心，那么设出点M坐标对于圆方程的表示更为简洁，运算也更为方便.因此，在解题时，运算的切入点选择也很值得关注.

解法2：设AP的中点为M，因为圆C上有且仅有一个点B满足AB⊥BP，所以以AP为直径的圆M和圆C相切.

设点M的坐标为M（t，t+2），则P（2t+2，2t+4），

切入点2（合理转化）：转化思想是将未知化为已知，复杂化为简单，非常规化为常规的思想方法.注意抓住问题的特征，合理转化，找到解题切入点，使问题简洁易解.

思路分析3（圆与圆的位置关系法3）：两圆相切是使用圆心距与半径之间的关系，不可避免用到根号与绝对值，运算量大且易错.抓住两圆对应方程作差确定点B所在的直线方程这一结论作为切入点，我们可以将两圆相切的问题转化为直线与圆相切，即点到直线的距离问题，从而快速解题.

解法3：设点P的坐标为P（t，t+2）.

因为圆C上有且仅有一个点B满足AB⊥BP，

所以以AP为直径的圆和圆C相切，

而以AP为直径的圆的方程（直径式）为（x+2）（x-t）+y（y-t-2）=0.

又圆C：（x-2）2+y2=2，两方程对应相减，

整理可得（t-6）x+（t+2）y+2t+2=0，

整理可得3t2-16t+5=0，解得t=或5.

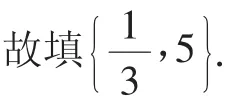
切入点3（展开联想）：拿到问题时，注意对题目中条件的结构，数据特征等展开联想，找到隐藏着的信息，常常能得到启发，找到解题的切入点.

思路分析4（双曲线法）：根据A（-2，0），C（2，0）关于原点对称，两圆相切又会得到圆心距等于半径和或差，展开联想，AP的中点M的轨迹与圆锥曲线有关，进而发现解题的切入点.

解法4：设AP的中点为M，因为圆C上有且仅有一个点B满足AB⊥BP，所以以AP为直径的圆M和圆C相切，可得||MA|-|MC||=＜4=|AC|，

切入点4（知识迁移）：数学的各部分内容不是孤立存在，而是互相渗透的.揭示和建立新旧知识联系，可以帮助我们发现问题的另一种表述，为高效率的解题找到切入点.

思路分析5（余弦定理法）：上述4种解法均没有跳出解析几何的框架，而题目中两圆相切得到圆心连线过B，从而将解析几何中的解点问题迁移到解△AMC的边AM，利用解三角形知识，顺利找到解题的切入点.

解法5：设AP的中点为M，因为圆C上有且仅有一个点B满足AB⊥BP，所以以AP为直径的圆M和圆C相切，设圆M的半径为r.

（1）当圆M和圆C外切时，在△AMC中，由余弦定理得MC2=AC2+AM2-2AC·AM·cos45°，

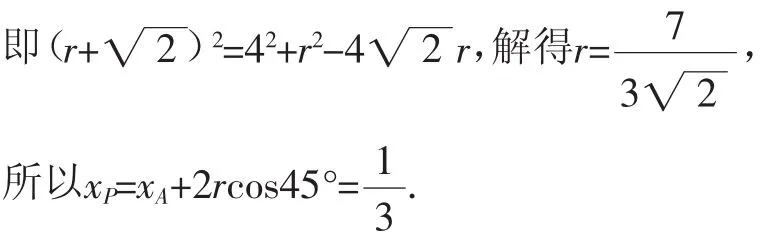
（2）当圆M和圆C内切时，在△AMC中，由余弦定理得MC2=AC2+AM2-2AC·AM·cos45°，

总结：根据圆C上有且仅有一个点B满足AB⊥BP来确定以AP为直径的圆和圆C相切，那么常见的思维方式就是利用两圆的位置关系来处理，可以通过不同的切入点来分析，解法1到解法3均从“两圆的位置关系的不同”这个角度来切入并处理；而根据以AP为直径的圆M和圆C相切可得||MA|-|MC||=＜4=|AC|，进而利用双曲线的定义来转化，结合直线与双曲线的位置关系来解决，解法4的思维巧妙，方法特别；由于涉及的是解析几何与三角形问题，当然离不开解三角形的方法，采取两圆外切与内切时的不同情况，利用余弦定理也可以达到非常有效的解答，解法5给出了解三角形的奇特应用.

总之，我们应当在仔细审题的基础上，分析问题与条件之间的关系，通过转化、联想、知识迁移等方法，找出解题的切入点.并在解题反思中注意对条件的充分挖掘，多角度出发，多方面求解，真正体现对数学知识的融会贯通，充分展现知识的交汇与综合，达到提升能力，拓展应用的目的.进而真正达到在学中“悟”，在“悟”中不断提升解题技能.正如我国著名数学家苏步青先生说过：“学习数学要多做习题，边做边思索，先知其然，然后知其所以然.”H