如何提升解题效率——以抛物线的焦点弦问题为例

☉江苏省启东市第一中学 宋凯东

抛物线的焦点弦问题一直是高考中的热点问题之一.在解决抛物线问题中，除了要熟练掌握抛物线的定义、方程、几何性质等内容，有时也要掌握一些常见的结论或公式，特别是有关抛物线的焦点弦的几条重要性质，在解决问题（特别是选择题或填空题）时，可以大大加快解题速度，在高考的宝贵时间内节省时间，提升解题效率，达到殊途同归、优化过程的目的.

一、焦点弦的定值问题

若AB是过抛物线C：y2=2px（p＞0）焦点F的一条弦，

例1 （2016·全国Ⅲ文、理·20（1））已知抛物线C：y2=2x的焦点为F，平行于x轴的两条直线l1，l2分别交C于A，B两点，交C的准线于P，Q两点.若F在线段AB上，R是PQ的中点，求证：AR∥FQ.

分析：常规方法是设出直线l1，l2的方程分别为y=a，y=b，进而确定相应点A、B、P、Q、R的坐标，同时求解直线AB的方程，结合点F在线段AB上得到关系式，从而确定直线AR、FQ的斜率来证明即可.而采用焦点弦的定值y1y2=-p2，可以有效简化运算，优化过程，提高效率.

解析：由抛物线C：y2=2x，可得p=1，则焦点准线方程为

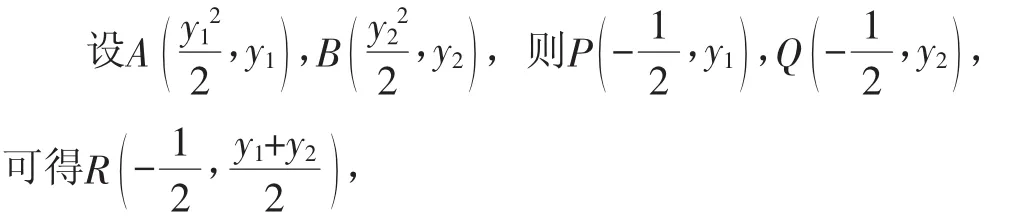
根据焦点弦的定值可知y1y2=-p2=-1，

所以AR∥FQ.

点评：利用抛物线中焦点弦的定值性质，可以有效转化抛物线中的焦点弦的相应点的坐标关系y1y2=-p2，巧妙地把相应的点的坐标与对应的参数p加以关联，直接略过相应的运算过程，减少了因运算能力薄弱而导致的错误，并有效加快解题速度，提升解题效益.

二、焦点弦的长度问题

若AB是过抛物线C：y2=2px（p＞0）焦点F的一条弦，且直线AB的倾斜角为θ，则有

例2 （2018·全国Ⅱ文·20（1），理·19（1））设抛物线C：y2=4x的焦点为F，过F且斜率为k（k＞0）的直线l与C交于A，B两点，|AB|=8，求l的方程.

分析：常规方法是设出直线l的点斜式方程y=k（x-1），与抛物线方程联立，转化为相应的方程，结合根与系数的关系，并利用抛物线的定义来确定对应的弦长，从而确定对应的参数k的值即可.而采用抛物线的焦点弦的长度公式可得进而通过确定直线l的倾斜角θ而求解对应的斜率，比较简单快捷.

解析：由抛物线C：y2=4x可得p=2，F（1，0），

所以直线l的方程为y=1×（x-1）=x-1.

点评：利用抛物线的焦点弦的长度公式来处理问题，可以避免函数与方程的繁杂计算，简化过程，直接利用三角函数以及直线的斜率定义来确定参数k的值，更为直接明确.碰到此类与焦点弦的长度有关的问题时，都可以考虑利用抛物线的焦点弦的长度公式来尝试与处理.

三、焦点弦的三角形面积问题

若AB是过抛物线C：y2=2px（p＞0）焦点F的一条弦，则△AOB的面积

例3 （2014·全国Ⅱ理·10）设F为抛物线C：y2=3x的焦点，过点F且倾斜角为30°的直线交C于A，B两点，O为坐标原点，则△OAB的面积为（ ）.

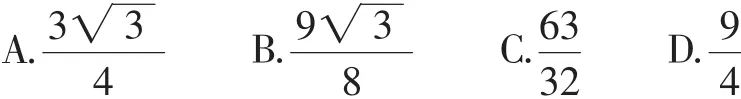
分析：常规方法是先确定|AB|的长度，并通过求解直线AB的方程，结合点到直线的距离公式求点O到直线AB的距离，从而得以求解△OAB的面积.而结合焦点弦的三角形面积来处理，可以“秒杀”.

解析：由抛物线C：y2=3x，可得p=.

又由题可得直线AB的倾斜角为θ=30°，

故选D.

点评：利用抛物线的焦点弦的三角形面积公式来求解，大大优化了解题过程，可以省去一些不必要的运算或求解过程，在解决此类问题的选择题或填空题中更具有优势.特别当涉及三角形的面积时，离不开弦长公式、三角形的高的运算，过程也较为繁杂，还容易出错.

四、焦点弦的圆的性质问题

若AB是过抛物线C：y2=2px（p＞0）焦点F的一条弦，以抛物线的焦点弦AB为直径的圆一定和准线相切.

例4 （2018·全国Ⅲ理·16）已知点M（-1，1）和抛物线C：y2=4x，过C的焦点且斜率为k的直线与C交于A，B两点.若∠AMB=90°，则k=______.

分析：常规方法是设出点A、B的坐标，利用点差法确定对应的直线的斜率，结合抛物线的定义加以转化，并利用梯形的性质加以求解.而利用抛物线的焦点弦的圆的性质，以抛物线的焦点弦为直径的圆一定和准线相切，从而可得AB⊥MF，“秒杀”求解.

解析：由于抛物线C：y2=4x，可得p=2，

则焦点F（1，0），准线方程为x=-1，

可知点M（-1，1）在抛物线C的准线上.

又由于以抛物线的焦点弦为直径的圆一定和准线相切，而∠AMB=90°，则点M恰为该切点，则可得AB⊥MF，

点评：采用抛物线的焦点弦的圆的性质，即以抛物线的焦点弦为直径的圆一定和准线相切，建立起对应直线的垂直关系，可以利用两直线垂直的斜率关系式来转化与应用，有效转化，提升效益.

课本上数学公式的推导都十分严谨！对不是课本公式而确实正确的结论，有时直接使用会起到事半功倍的效果.特别对小题（填空题、选择题）更要防止走入“小题大做”误区.这说明数学上的直接思维，或者看似比较复杂问题而直接能得出答案的能力，是需要的而且是可以培养的.

所以，在平时学习过程中，有意识地熟练掌握一些有关抛物线的相关性质，特别是抛物线的焦点弦的性质，既是对抛物线的定义、方程与几何性质的深入理解与掌握，又是对相关知识的拓展与深化.有时命题者可能对题目作了某种程度的改头换面，或者适当的变式与包装，只要抓住关键词“焦点弦”三个字，就可以有效利用抛物线的焦点弦性质来解决问题，这样可以减少解题时间，简化解题步骤，优化解题过程，弱化解题误区，全面提高数学效益，培养数学素质，提升思维品质.F