双变量不等式证明策略——从2018年全国Ⅰ卷导数题说起

☉江苏省徐州市第三十六中学 袁克政

一、命题评析

（1）讨论（fx）的单调性；

（2）若函数（fx）存在两个极值点x1，x2，证明＜a-2.

本题是以导数为背景的双变量不等式问题，较为常规，但作为压轴题，对考生的思维能力及运算能力要求较高.笔者初见此题有似曾相识之感，研究发现，此题源于2011年高考湖南卷文科第22题：

（1）讨论函数f（x）的单调性.

（2）若函数f（x）有两个极值点x1，x2，记过点A（x1，f（x）），B（x2，f（x2））的直线的斜率为k，问：是否存在实数a，使得斜率k=2-a？如果存在，求出a的值；如果不存在，请说明理由.

对往年高考题进行变式，也是高考命题的依据，从两道题目的已知函数及问题设置来看，2018年全国卷Ⅰ理科第21题是将2011年湖南高考文科第22题进行推陈出新.

二、问题解答

题目中的两个变量为已知函数的两个极值点，因此两个变量之间必然存在某种关系，挖掘出这种关系，是问题顺利求解的关键一步.

解析：（1）函数f（x）的定义域为（0，+∞）.

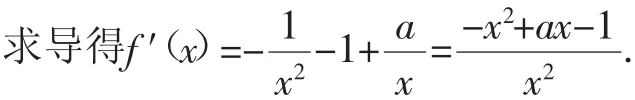
当Δ=a2-4≤0，即-2≤a≤2时，f′（x）≤0，所以函数f（x）在（0，+∞）单调递减；

当Δ=a2-4＞0时，a＜-2或a＞2. 若a＜-2，0，且＜0，所以在（0，+∞）内，f′（x）≤0，函数f（x）在（0，+∞）上单调递减；若，所以在区间（0，x1），（x2，+∞）内，f′（x）＜0，函数f（x）单调递减；在（x1，x2）内，f′（x）＞0，函数f（x）单调递增.

综上，当a≤2时，f（x）在（0，+∞）上单调递减；当a＞2时，函数f（x）在区间f′（x）＜0，函数f（x）单调递减；在内，f′（x）＞0，函数f（x）单调递增.

（2）方法1：由（1）知，当a＞2时，函数f（x）存在两个极值点x1，x2.由根与系数的关系知，x1x2=1.

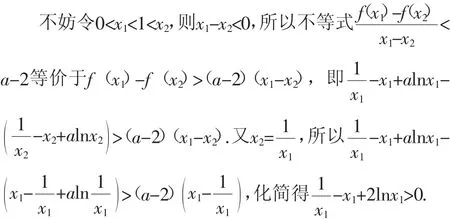
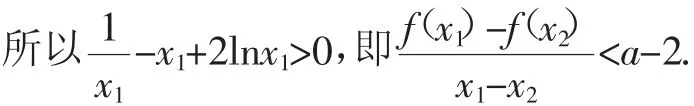
问题得证.

方法2：由（1）知，当a＞2时，函数f（x）存在两个极值点x1，x2.由根与系数的关系知，x1+x2=a，x1x2=1.

评析：上述两种思路殊途同归，但思路2目的性更强，通过所给条件，利用根与系数的关系，找到两个变量之间的关系.从而实现了将双变量化为单变量求解.

三、变式拓展

变式1：已知f（x）=（a+1）lnx+ax2+1.

（1）求f（x）的单调区间；

（2）设a≤-2，证明：对∀m，n∈（0，+∞），|f（m）-f（n）|≥4|m-n|.

解析：（1）函数f（x）的定义域为（0，+∞）.

当a+1≤0，即a≤-1时，在区间（0，+∞）内f′（x）＜0，所以f（x）在（0，+∞）上单调递减；

当a＜0且a+1＞0，即-1＜a＜0时，令f′（x）=0，得x=f′（x）＞0，f（x）单调递增；在区间＜0，f（x）单调递减.

当a≥0时，在区间（0，+∞）内f′（x）＞0，所以f（x）单调递增.

综上，当a≥0时，f（x）在（0，+∞）上单调递增；当a≤-1时，f（x）在（0，+∞）上单调递减；当-1＜a＜0时，f（x）递减.

（2）不妨设m＞n，而a≤-2，由（1）可知，f（x）在（0，+∞）单调递减，从而对∀m，n∈（0，+∞），要证|f（m）-f（n）|≥4|m-n|，只需证f（n）-f（m）≥4（m-n），即f（n）+4n≥f（m）+4m.

令g（x）=f（x）+4x，则

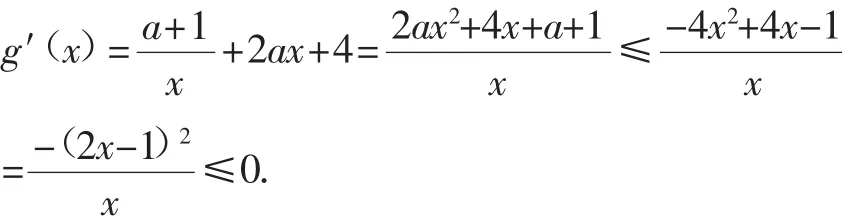
故g（x）在（0，+∞）上单调递减，所以f（n）+4n≥f（m）+4m，即|f（m）-f（n）|≥4|m-n|.问题得证.

评析：注意到所证不等式f（x2）-f（x1）≥4（x1-x2）结构特征，通过构造函数g（x）=f（x）+4x，将两个变量合二为一，进而将所证不等式转化为判断新函数的单调性求解.

（1）若函数f（x）在（0，+∞）上为单调增函数，求a的取值范围；

（2）设m，n∈R+，m≠n，求证：

解析：（1）函数f（x）的定义域为（0，+∞），

因为f（x）在（0，+∞）上为单调增函数，所以f′（x）≥0在（0，+∞）上恒成立，即x2+（2-2a）x+1≥0在（0，+∞）上恒成立.

当x∈（0，+∞）时，由x2+（2-2a）x+1≥0，

所以2a-2≤2，即a≤2.

综上，a的取值范围是（-∞，2］.

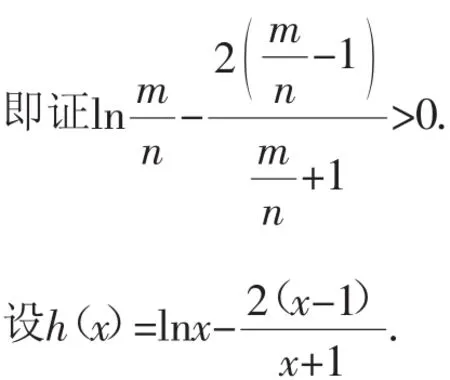
由（1）知，当a=2时，h（x）在（1，+∞）上是单调增函

评析：本题在求解中通过转化变形、整体换元，将双变量合二为一，进而构造新函数，将所证不等式转化为求新函数的最值问题处理.

通过对以上几例的分析与求解，不难发现，双变量不等式问题求解的关键是将两个变量合并为一个变量，再构造新函数，利用新函数的性质.另外此类问题还有一个共同特点，即构造的新函数都与已知函数有关，且新函数的性质在前一问中已经得出，因此求解中要注意前后问之间的关联.H