复合地基下卧层沉降的黏弹性分析

陈 凡，祝彦知，纠永志

(中原工学院 建筑工程学院，河南 郑州 450007)

随着复合地基理论的不断发展和完善，复合地基的沉降理论已经被提至重要位置。复合地基沉降可近似看作加固区与下卧层的沉降之和。目前对于加固区沉降计算的研究较多，文献[1]根据以往的研究成果[2-5]首次考虑了桩土的相互作用，获得了端承刚性桩加固区沉降的解析解；文献[6]针对成层土，应用弹性理论推导了路堤荷载下加固区桩及桩周土压缩量计算的理论解；文献[7]考虑上部填土的土拱效应和桩土荷载传递性状，推导出了复合地基加固区沉降变形解析式；文献[8]在文献[7]基础上既考虑填土的土拱效应，又考虑到桩周土体成层性，给出了一种更合理的路堤荷载下复合地基沉降计算解析表达式。

对于下卧层来说，沉降变形在总沉降中占相当大的比例。如公路引河大桥桥头和过渡段采用二灰土桩加固,其某断面沉降的实测沉降值为：加固区的变形量S1=15.7 cm；下卧层的变形量S2=33.4 cm[9]。土体的非线性应力与应变关系,使下卧层土体的性质成为沉降的重要影响因素。因此，本文在文献[10]引入修正系数计算方法的基础上，将土体黏弹性特征引入复合地基下卧层的沉降计算中，选择三参数固体模型来描述土体本构关系，推导矩形截面上均布荷载下复合地基下卧层沉降的黏弹性计算式，并根据计算式的解答编制相应的计算程序，最后通过实测对计算结果进行验证。

1 下卧层沉降的黏弹性解

针对图1所示的复合地基沉降问题，大部分文献将复合地基分为加固区和下卧层两部分，总变形为加固区的变形量S1和下卧层的变形量S2两部分之和。本文假设褥垫层的沉降很小，可忽略不计。

图1 复合地基沉降示意图

土体的变形规律采用流变性来表示，既有弹性,又有黏性。一根弹簧和一个Kelvin模型串联(见图2)，能够较好地模拟岩土体受力变形的黏弹性状态，且比较简单，较常用。在标准的线黏弹性固体模型中，组合元件的数目越多，越能够真实地反映黏弹性材料的实际特性。三参数固体模型能够反映一般线黏弹性土体的全部特征，因此本文以三参数固体模型作为分析模型。三参数固体模型本构方程如下：

(1)

式中：σ为正应力；ε为应变；G1、Gk分别为图2所示三参数固体模型中两个弹性体的弹性模量；ηk为黏性系数。

图2 三参数固体模型

2 空间半无限体的黏弹性解

2.1 矩形截面上竖向均布荷载引起的内部角点处黏弹性沉降

在图3所示的矩形截面上均布荷载下角点处沉降计算示意图中，当半无限体内部深为h处作用一竖向均布荷载p时，由文献[11]可知，此时引起角点O处竖向位移(沉降)的黏弹性解答如下：

8a5(v5-v6a3-v7a2)+a7(v4-v2a3+v3a1)]

(2)

式中：

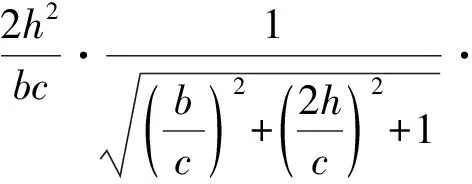
式中：p为均布荷载；b、c分别为矩形截面的长度和宽度；K为体积模量；Gk、G1、K、ηk均为黏弹性参数。

图3 矩形截面上均布荷载下角点处沉降计算示意图

2.2 黏弹性半无限体表面均布荷载时角点处竖向位移

均布荷载下黏弹性表面所引起的角点处竖向位移的最终计算结果如下(限于篇幅，本文只给出黏弹性竖向位移的最终计算结果)：

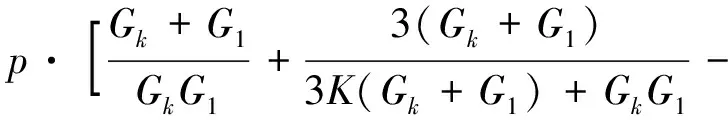
(3)

2.3 矩形截面上均布荷载下中心点处沉降的黏弹性解

在图4所示的矩形截面上均布荷载下中心点处沉降计算示意图中，半无限体内部作用竖向均布荷载所引起的内部中心点处竖向位移的黏弹性解答如下：

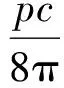
8b5(v5-v6a3-v7a2)+b7(v4-v2a3+v3a1)]

(4)

式中：

2.4 黏弹性半无限体表面均布荷载时中心点处竖向位移

均布荷载下黏弹性表面中心点处竖向位移的最终计算结果如下：

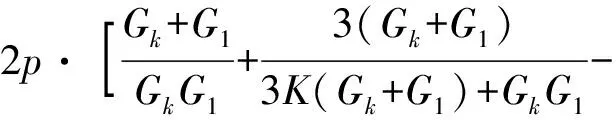
(5)

图4 矩形截面上均布荷载下中心点处沉降计算示意图

3 引入土体黏弹性的下卧层沉降计算

本文利用半空间体竖向均布荷载的位移黏弹性解，根据文献[10]的修正系数，考虑下卧层土体的黏弹性，对下卧层沉降的理论解进行推导。

半空间体内部竖向均布荷载的角点处位移黏弹性解(即式(2))与半空间体表面竖向均布荷载的角点处位移黏弹性解(即式(3))的比值写作e1。

(6)

式中：

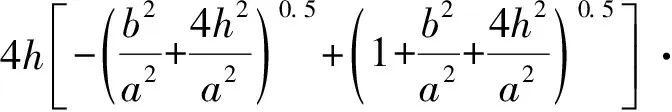
半空间体内部竖向均布荷载的中心点处位移黏弹性解(即式(4))与半空间体表面竖向均布荷载的中心点处位移黏弹性解(即式(5))的比值写作e2。

(7)

式中：p1、p2表达式同e1；

对e1和e2取平均值得到k值(修正系数)，然后乘以式(5)，最后代入具体参数，即可得到下卧层沉降。

4 工程实例分析

本文选用文献[12]中实例进行对比分析。上海某小区采用粉喷桩加固地基，其土层概况如表1所示。复合地基设计承载力为100 kPa，设计桩长度为14 m，桩径为0.5 m，加固面积为74×16 (m2)，置换率为15%，房屋竣工后实测稳定沉降的平均值为102 mm。

土体黏弹性参数取值如表2所示。根据本文计算方法编制了相应的计算程序，计算得到的k值为0.76，下卧层的沉降为45.7 mm，最终得到的复合地基总沉降为100.1 mm。显然，沉降计算值与实测值十分接近。采用各类方法所得沉降值对比如表3所示。

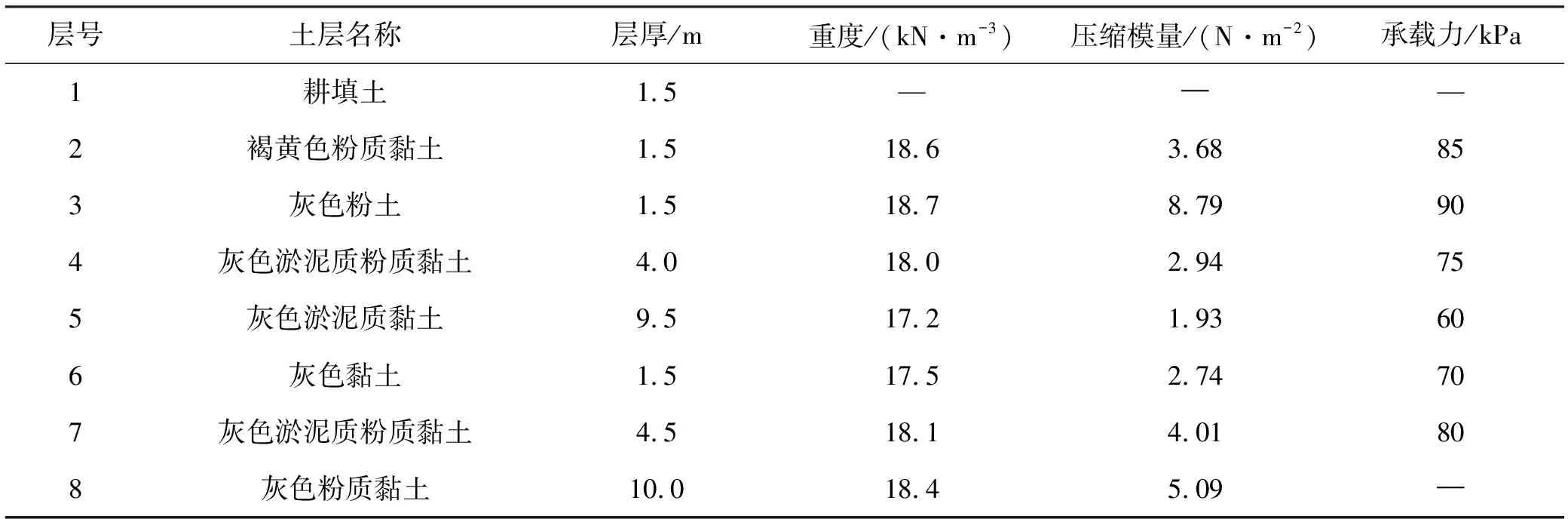
表1 土层概况

表2 土体黏弹性参数取值

表3 各类方法沉降计算值的比较 mm

为了方便对比，本文分别取h为10 m、12 m、14 m，对下卧层沉降及修正系数k进行计算分析；分别取黏性系数ηk为200 MPa·d、2 000 MPa·d，再次对下卧层沉降及修正系数k进行计算分析。埋深h变化时修正系数和下卧层沉降随时间的变化曲线分别如图5和图6所示。黏性系数ηk改变时修正系数和下卧层沉降随时间的变化曲线分别如图7和图8所示。

图5 埋深h改变时修正系数k随时间的变化曲线

图6 埋深h改变时下卧层沉降y随时间的变化曲线

由图5和图6可以看出，当埋深由10 m逐渐增大到14 m时，修正系数及下卧层沉降的黏弹性解逐渐减小，然而二者的变化趋势没有太大差异。

由图7和图8可以看出，当黏性系数增大10倍时，修正系数及下卧层沉降黏弹性解的曲线明显趋于平缓，对二者的曲线变化趋势影响较大，但最终的趋向值差别并不明显。在计算复合地基沉降时，特别是对于软土地基来说，黏弹性特征表现得很明显，黏弹性参数取值及荷载面埋深对于复合地基下卧层沉降黏弹性解的影响明显不同，因此在计算下卧层沉降时必须考虑这一点。

与文献[10]的结果相比，本文计算方法引入土体黏弹性，计算结果更接近下卧层沉降的实测值。

图7 黏性系数不同时修正系数k随时间的变化曲线

图8 黏性系数不同时下卧层沉降y随时间的变化曲线

5 结 论

(1) 本文给出了以三参数固体模型为土体本构关系的复合地基下卧层沉降的黏弹性解答，计算结果更接近于实测值。

(2) 对流变性明显的软土地基来说，不考虑黏弹性与考虑黏弹性的分析比较表明，考虑黏弹性更加符合工程实际情况。

(3) 以三参数固体模型模拟岩土体的黏弹性特征，结果表明，土体黏弹性参数取值及荷载面埋深对复合地基沉降黏弹性解的影响是不同的，在计算下卧层沉降时应予以考虑。