带有死区输入的非线性切换系统的自适应模糊控制

李雷雷

(山东科技大学 数学与系统科学学院, 山东 青岛 266590)

近几年，对于控制未知非线性系统，经常使用模糊逻辑系统和神经网络方法近似该系统中的未知非线性函数。基于模糊逻辑系统和神经网络，许多自适应控制方案已被提出，如文献[1-3]。最近，一些学者结合模糊逻辑系统方法，将自适应反推技巧引入到切换非线性系统中，并提出了一些任意切换形式下的不定非线性系统控制方案，如文献[4-6]。

众所周知，死区是控制系统中常见的一种外部干扰，它常导致系统不稳定。最近，关于死区的控制系统，同样引起了人们广泛的关注，如文献[7-12]。其中Wang X S等提出了一种有效的自适应控制方案，消除了死区对非线性控制系统的影响[8]；针对一类带有死区的非严格反馈系统，Wang L J等通过设计一个带有观测器的自适应控制方案来解决死区干扰问题[9]；针对一类带有死区的连续时间非线性控制系统，基于模糊近似和反步法技巧，Liu Y J等提出了一种自适应模糊控制方案，消除了死区对系统稳定性的干扰[10]；对于一类带有死区和不可测状态的单输入单输出不定非线性系统，Liu Y J等设计了一个带有观测器的自适应模糊控制方案[11];通过应用自适应反步法设计技巧、模糊滤波状态观测器和死区逆方法，针对一类不定严格反馈非线性系统，Tong S等提出了一种自适应模糊控制方案，保证了系统的稳定性[12]。

由于现代技术的不断升级和优化，切换系统也引起了人们的广泛关注。有不少好的控制方案被提出，如文献[13-14]。其中李雷雷等设计了一个任意转换下带有未知迟滞的随机非线性系统自适应跟踪控制方案[14]。

基于以上研究成果，本文研究了一类带有死区的非线性切换系统的自适应跟踪控制，通过设计相应的自适应控制器，选择合适的李雅普诺夫函数，构造一个自适应观测器，结合反步法技巧，提出了一个自适应模糊控制方案。该方案保证了系统所有的信号半全局一致最终有界。

1 问题分析

非线性随机纯反馈系统为：

(1)

(2)

其中v表示死区输入，mr、ml、cr和cl都是未知的正常数。为了完成反步法控制方案，引入下面的假设和引理。

假设1:存在一个正的常数A，使得|v|≤A。

引理2(杨氏不等式):对∀(x,y)∈R2,有

(3)

其中ε>0,p>1,q>1,并且(p-1)(q-1)=1。

式(2)的输出能够被表示成下列形式

u(t)=m(t)v(t)+d(t)

(4)

因此，能够得到

(5)

(6)

把式(6)代入式(4)，得

(7)

则系统(1)能够写成：

(8)

把式(7)代入式(8)中，得

(9)

2 控制方案设计

这里将设计一个状态观测器。基于反步法和模糊逻辑系统近似,针对系统(1)给出一个自适应模糊控制方案。

设计状态观测器形式如下：

(10)

同样，我们可以把所设计的状态观测器写成状态空间形式:

(11)

(12)

选择恰当的李雅普诺夫函数形式V0=eTSe。则它的微分

(13)

定义

(14)

(15)

把式(15)代入式(14)得

(16)

(17)

同时，根据假设1，下列不等式成立

(18)

(19)

结合式(16)、(17)、(18)、(19)和(13)，则有

(20)

基于反步法技巧，下面给出一个自适应模糊控制方案。反步法需要n步，在设计过程中,构造虚拟控制信号αi(i=1,2,…,n-1)

(21)

实际控制信号

(22)

自适应参数

(23)

其中：ri>0；σi>0。

在反步法的每一步中将用到下列坐标变换

(24)

第1步：根据坐标变换和式(10)，z1的时间微分为

(25)

构造李雅普诺夫函数

(26)

则有

(27)

利用杨氏不等式(3)，有

(28)

把式(28)代入式(27)中，得

(29)

(30)

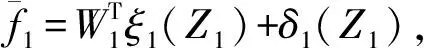
(31)

代入式(30)得到

(32)

把式(21)代入式(32)得

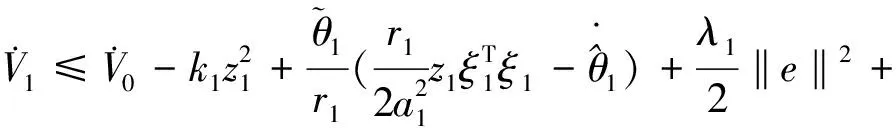
(33)

再把式(20)和式(23)代入式(33)得

(34)

依照同样的步骤，结合式(21)、式(22)和式(23)，进行第2至n步的运算，得到结果为：

(35)

3 稳定性分析

根据杨氏不等式(3)得

(36)

代入式(35)得

(37)

定义

(38)

(39)

该公式等价于

(40)

故可以假设存在正矩阵S,使得下列不等式成立

(41)

因此，可以推出一个常数γ>0，使得

(42)

其中λN(S)为矩阵S的最大特征值。把式(42)代入式(37)得

(43)

(44)

由式(34)、(35)和(44)可知，对于i=1,2,…,n，自适应控制系统(1)中的所有信号半全局一致最终有界。

根据以上分析和讨论，我们得出以下结论：

在假设1和假设2的条件下，对于带有死区输入的非线性切换系统(1)，利用反步法技巧结合模糊逻辑系统近似，通过构造恰当的李雅普诺夫函数(26)，设计状态观测器(10)、虚拟控制信号(21)、实际控制信号(22)及自适应律(23)，保证了闭路控制系统(1)的所有控制信号半全局一致最终有界。

4 结 语

基于一系列带有未知死区的严格反馈非线性切换系统，提出了一个基于观测器的自适应模糊控制方案。本文利用模糊逻辑系统近似识别系统中的未知函数，构造一个恰当的李雅普诺夫函数，结合自适应反步法，设计控制信号和自适应参数，保证了闭路控制系统(1)的所有控制信号半全局一致最终有界。