基于环形周向多点差压法的风速风向测量研究

盖增杰，周伟，刘海军，李春国，闫宏凯，刘斌

（1.中国中车青岛四方机车车辆股份有限公司，山东青岛266111；2.中南大学交通运输工程学院，湖南长沙410075；3.中国铁路乌鲁木齐局集团有限公司，新疆乌鲁木齐830011）

风区铁路列车运行的车载风速测量一直是列车防风安全研究的热点问题.针对列车行经风区的防风安全评估，目前主要参考列车所经铁路沿线测风站时的地面监测风速作为依据，而由于风区地形地貌复杂，远方来流经地形突变后在列车运行线路位置往往变化较大，并不能有效表征列车实际承受的服役风载[1-4].因此，亟待提出一种车载式的二维风速风向测量方法，准确评估列车运行过程中的服役环境风速.

针对环境风速的测量，目前广泛采用的有机械式、超声波式、热线式等.机械式风速仪的风速测量元件为螺旋桨或风杯，风向测量元件为风向标，其螺旋桨或风杯的转速与风速成正比.机械式传感器因其结构简单、低成本，是目前应用最广泛的.但该类传感器最大缺点是存在机械磨损.

超声波风速仪因其高采样率、实时性、高精确度，并且不存在旋转部件，得到广泛应用，但由于超声波的传输距离必须要远大于超声波传感器的尺寸，限制了超声传感器小型化.

热线式或热场式风速仪在测量低速流动时，特别是在要求高空间分辨率的测量场合，比机械式风速仪更有优越性.热式风速仪不存在机械磨损，其尺寸可以做到很小，但热式传感器暴露在空气中的热量元件非常脆弱，很容易损坏.

国内外学者针对基于多点感压的测速开展了系列研究.Bruschi等[5]通过在圆柱体上设计固定通道，基于热流量测量差压得出圆柱侧面差压压力分布与风向的余弦函数关系，设计当使用两个相同的结构并正交放置时，可同时获得风速和风向.此方法在风速范围0.9～8.4m/s 内具有较高的效率，但雨水、沙尘会通过空气进入到通道内，对流量测量元件造成损害.

C.Liu等[6]提出一种利用四组差压传感器测量风速风向的圆柱形设备，围绕圆柱体侧面均匀布置8个小孔，同一直径上的两个孔为一组，并通过导压管连接差压传感器，圆柱体将传感器与气流隔离开.文献[6]指出：忽略尾流扰动时，差压传感器数值与动压的比值在一定范围内与雷诺数无关.并由此计算出风速风向；试验结果表明：在风速0.91～39 m/s 时传感器具有较高的可靠性，但当风速超过39m/s或传感器直径改变时，文献方法不再适用.

通过测量不同形状物体表面压力分布计算流体的特性的技术正在快速发展.基于该技术，我们设计了一种利用空气压力传感器获得风速风向数据的二维圆柱形风速仪，且该风速仪不受自身尺寸大小的约束.在所设计的风速仪圆周上，均匀分布12个小孔，每个小孔连接一个空气压力传感器.当风向改变时，迎风侧相邻三个压力传感器的数值变化满足一定函数关系.通过环周向二次压力分布关系推导得到风向，并由风向和压力值得到风速.由于只考虑迎风侧的压力值，背风侧涡流干扰不会对其造成影响，因此风速仪直径改变时，该方法同样适用.

1 测试原理

本文的风速测量仪采用在圆柱表面上设置 12个感压点，测量各感压点最大的三个压力点及对应位置，计算来流的风速和风向.本节主要针对测点的布置方式和样机的设计展开介绍.

1.1 测点布置

根据圆柱绕流原理，二维圆柱低速定常绕流的流型只与雷诺数有关，如图1所示.由于尾流涡旋的影响，利用圆柱面对称点差压方式计算流体流速，如图1-a的P+1与P-1、P+2与P-2、P+3与P-3，雷诺数Re较大时已经不能代表其实际流速.因此采取如图1-b所示的分离点前圆柱避免压力分布计算方法，以圆柱全封闭稳压腔的压力作为参考压力，可以准确计算流体流速，且设计模型不受直径大小影响.

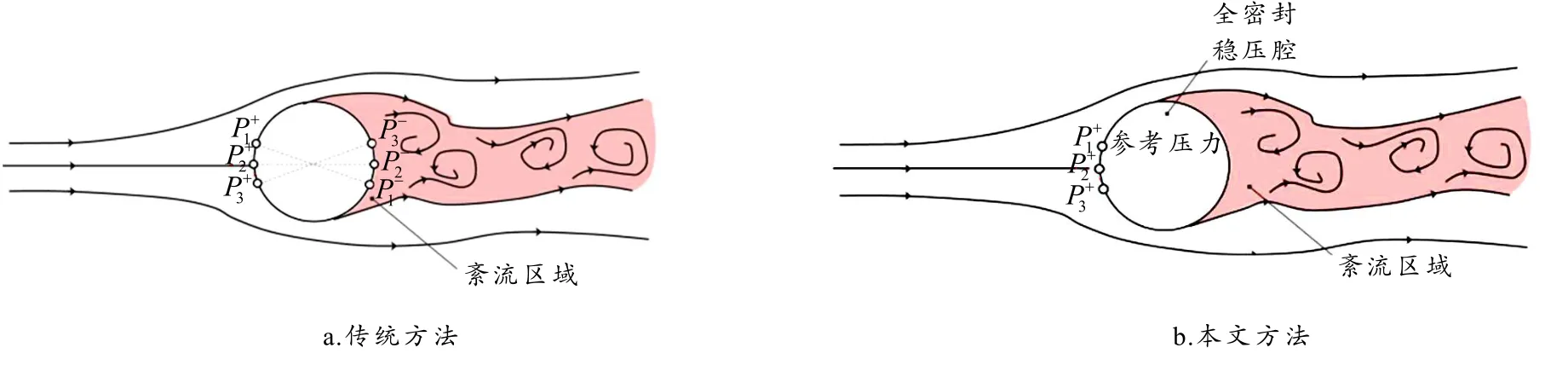
图1 不同风速测量原理比较

在圆柱体表面环周向等间距设置 12个压力测点，相邻测点之间夹角为30°.在稳定的空气流中，圆柱体表面某一点的压力Pθ随着角度变化而变化，但总能找到压力最大的 3个点 1#、2#和 3#.如图2所示，以2#传感器为参考点，当风向在15±°之间改变时，三个压力传感器的值P1、P2、P3都会随之改变.本文的研究重点是找出P1、P2、P3与风速风向之间的关系，并计算得出风速风向.

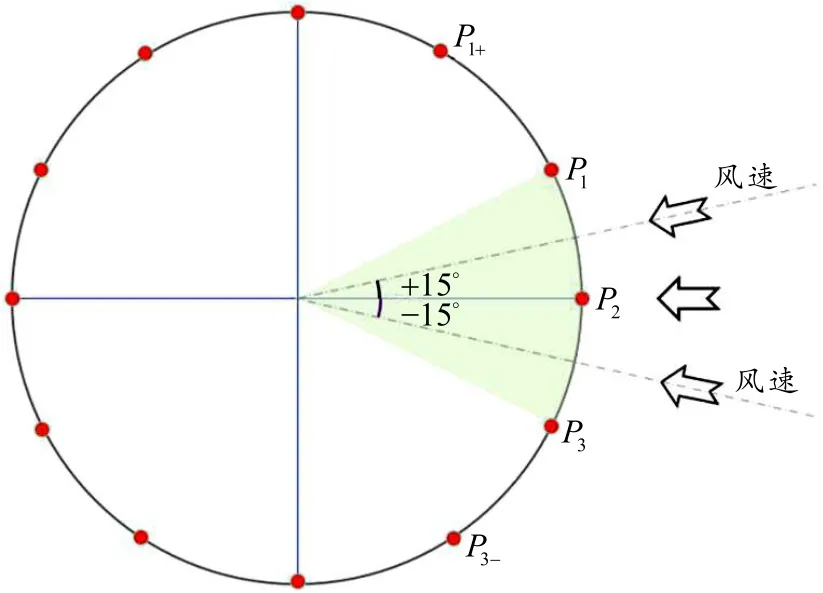
图2 3极值压力点及风向变化区域示意图

1.2 样机设计

按照上述测点布置方案，本文设计并制作了一个风速仪，如图3所示，圆柱直径为100 mm，高400 mm，孔位置高300 mm，顶部为半径50 mm的半球体.

由图3可以看出，12组孔均匀分布在圆柱侧面，每组孔由3个直径为1 mm的小孔垂直排列而成，气流通过小孔进入密闭腔体，我们称之为感压腔，并通过感压腔上的导管连接至差压传感器的正端，差压传感器和电路芯片安装在圆柱体内，避免了敏感元件位于空气中受腐蚀的问题.多个小孔垂直排列不仅提高敏感度，有效防止感压孔因沙尘、雨水而堵塞.每个感压孔连接一个差压传感器的正压口，所有差压传感器的负压口相互连通至同一个参考压，参考压一般为大气压，多个差压传感器互不影响.

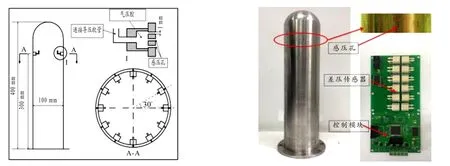
图3 风速测试样机原理图及实物图

风速仪样机设计参数如下：

1）压力值与风速的平方成正比，传感器的选择必须满足大量程、高精确度.因此选取 M191D型数字差压传感器，传感器量程为3kPa±，最大可测风速可达68m/s.

2）在嵌入式程序中对数据进行处理.传感器输出数字信号，将其转换为压力值后根据公式计算得出风速风向值.传感器反应时间为1.5 ms，因此最大的采样频率为666 Hz，在本程序中设置数据采集频率为10 Hz，并求取平均值得到 1s数据，这样能减少突变和采样点缺失对数据的影响.同时计算3 s平均风速风向值，最大限度减少随机误差的影响.

3）该传感器包括12个空气压力传感器，因传感器的零点不同，因此在数据计算之前需要在零漂条件下对每个传感器进行零点采集，并将零点数据保存在闪存中.当需要对传感器重新采集零点时，只需要调用MCU中的程序即可.

4）硬件电路设计时，将控制部分与传感器部分分开，这样同一个控制电路可以匹配多个传感器电路，只需重新采集传感器零点并保存即可，反之亦然.

2 测试模型

通过风洞试验验证风速风向的测试模型.将风速仪样机安装在测角仪上，在标准风洞中旋转测角仪模拟风向改变的状态，以5°为一个间隔角度，沿圆周方向旋转360°，在每个感压孔的15±°范围内，该感压孔均为风压极值点P2，总计12个测点，每个测点占用30°的旋转工况，总计完成360°的周向旋转工况，相当于3极点风压测试工况进行了12次重复性试验.来流风速40 m/s条件下，对12次重复性试验的数据进行平均以消除测量误差，得到 3极点风压平均值，由公式（7）、（8）、（9）和参数S计算值如表1所示.

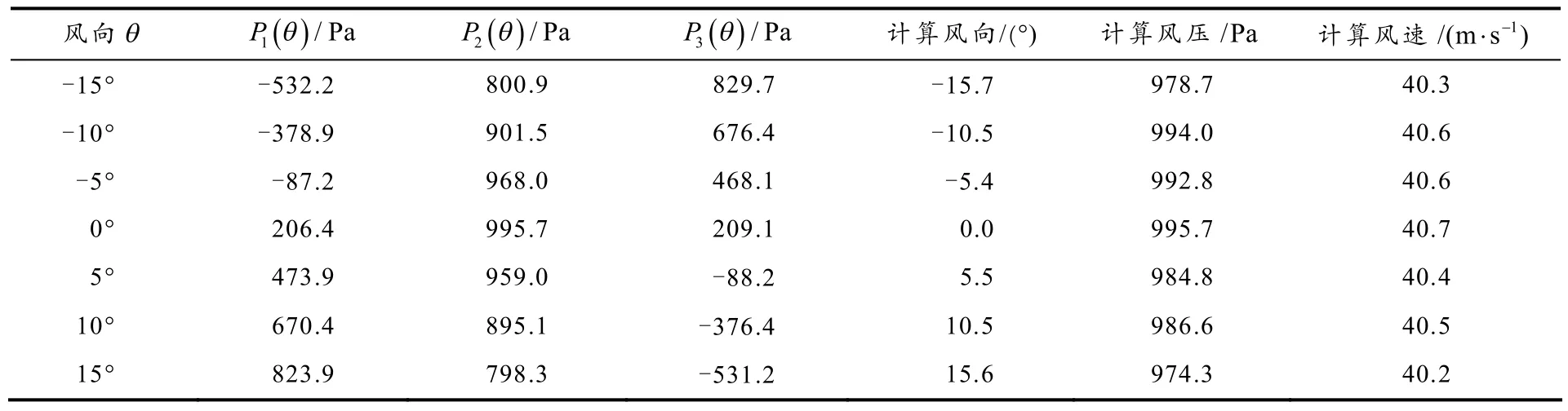
表1 不同风向角下3极点风压试验平均值及计算参数值

由表1的风洞标定数据代入测试模型的风速风向计算结果与给定来流的风速风向进行对比可知，风向的计算误差不超过0.7°，风速的计算相对误差不超过1.75%.

3 试验验证

3.1 试验方案

为了测试试制传感器的准确性，将其置于中南大学风速风向传感器标定风洞中进行试验，并将试验结果与Cobra 270风速仪进行对比.风洞的高速段其截面尺寸为0.8 m1.0 m×，长度为3.4 m，风洞最大风速和最小风速分别为60 m/s和5 m/s.风洞试验段具有较好的稳定性，速度稳定性不大于0.5%，局部气流偏角不大于0.8°，且湍流度不大于 0.8%.传感器在风洞中的安装如图4所示，传感器固定在测角仪上，位于风洞正中央，测角仪的旋转角度通过电脑进行精确控制.测角仪带动传感器旋转，模拟风向角改变.风速大小是由风洞进行控制，控制精度为0.1 m/s.传感器的输出风速风向通过通讯线传输至电脑上并显示.

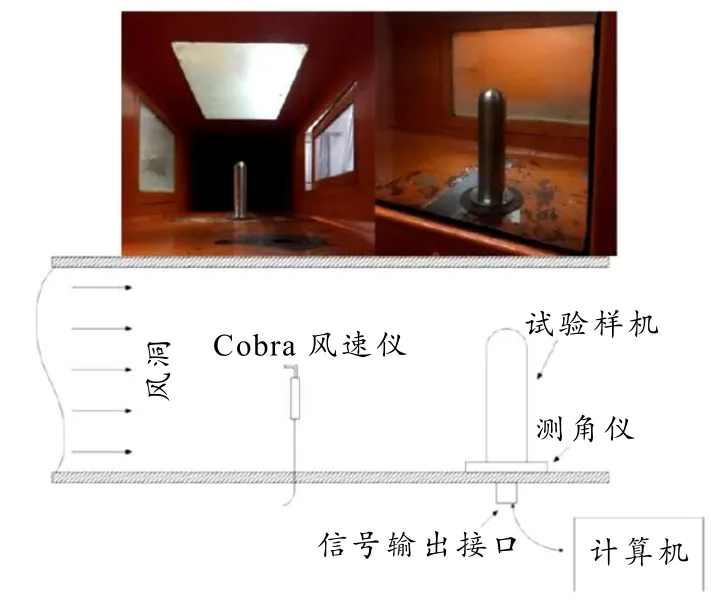
图4 风速测试样机风洞标定试验

3.2 误差分析

在5～60 m/s范围内以5 m/s为间隔逐步进行多组风速试验，在每个风速等级下，以10°为间隔旋转传感器，得到传感器的风速风向数据，并与参考风速风向进行对比，计算相对误差比.测量风速与参考风速之间的相对误差不超过4%，如图5所示.测量风向与测角仪读数之间的误差不超过4°，如图6所示.

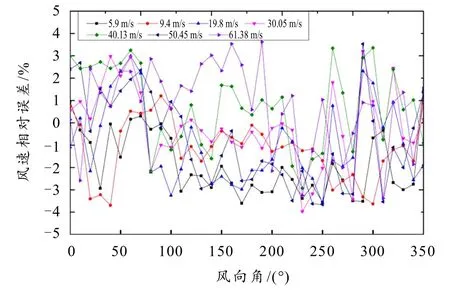
图5 风速测量相对误差

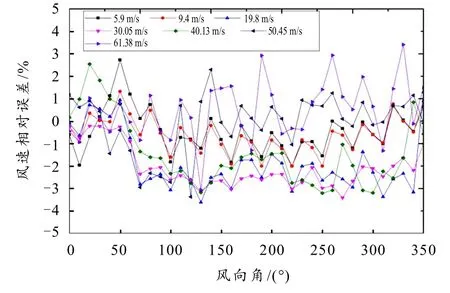
图6 风向测量误差

4 结论

本文提出一种利用差压传感器测量多点压力的二维风速风向测量技术.风速仪位于空气流中时，风速仪圆周上每一点压力值均与风速大小有关，本文的关键点在于研究压力在圆柱上的分布与风速之间的关系，并用公式进行表达，最终根据该公式通过压力值计算得到风速风向值.

根据本文的研究成果，设计制造直径为10 cm的风速仪，并在风洞中进行试验，试验风速范围为5 ～60 m/s.试验结果表明，风速相对测量误差不超过4%，风向测量误差不超过4°.

本文研究压力与角度之间的关系时，选取±15°的范围.由图3-a可知，当角度扩大至±20°时，D与θ仍具有较好的线性关系，此时只需要 9个传感器就可以计算得到风速风向.当改变模型的直径时，所需传感器个数能否更少是本文需要进一步做的研究.