宇宙波函数的动力学解释及应用
2018-09-13何东山
何东山
(咸阳师范学院 物理与电子工程学院,陕西 咸阳 712000)
天文观测表明现在的宇宙正在不断地膨胀[1],根据广义相对论得到的宇宙大爆炸理论,得到科学家们的广泛认同,因此大爆炸模型也被称为宇宙学的标准模型。大爆炸理论表明宇宙从一个温度极高、能量密度极大的奇点演化而来,在奇点处物理量发散,物理定律在奇点处失效。而量子理论表明,早期宇宙的量子效应显著,应运用量子引力理论来描述早期宇宙的演化。
引力的量子化仍然是理论物理研究领域的一个难题,目前人们提出的量子引力理论有弦理论、圈量子引力理论、惠勒-德维特方程等。虽然还没有一个完整、确定的量子引力理论。但是,通过研究一些初步的量子引力理论取得了一些有意义的结果。20世纪80年代开始Hawking、Hartal、Vilenkin、Linde等人将惠勒-德维特方程应用于宇宙学[2-5],来研究宇宙的创生以及暴涨等问题,本文作者及其合作者曾利用惠勒-德维特方程给出了无需标量场的暴涨模型[6-8]。量子力学中,量子系统的量子态由满足薛定谔方程的波函数描述。哥本哈根学派将波函数ψ()r的平方解释为粒子在空间r处的概率密度。与薛定谔方程在量子力学中的作用类似,惠勒-德维特方程是量子宇宙学的基本方程,宇宙的信息包含于满足惠勒-德维特方程的宇宙波函数中,因此很容易想到用宇宙波函数ψ的平方表示宇宙在超空间的概率密度[9],

然而对于宇宙来说这样的解释存在观测上的困难,人类所处的宇宙只有一个,因此无法用概率诠释来描述宇宙。根据哥本哈根诠释,每观测一次波函数就会坍缩,而对于人类所处的唯一的宇宙来说无法通过多次实验观测来确定宇宙处于某个状态的概率。因而,在量子宇宙学中波函数的统计诠释存在观测困难。
本文在小超空间模型下,研究了波函数的物理意义,给出宇宙波函数的动力学解释;通过宇宙波函数收敛的要求给出算符次序因子 p的取值约束;最后,宇宙波函数的动力学解释表明Hawking给出的无边界波函数在宇宙很大时给出的是一个定态解,宇宙无法演化,而Vilenkin的隧穿波函数给出了正确的宇宙演化规律。
1 惠勒-德维特方程
1967年DeWitt提出了一种对广义相对论正则量子化的方法[10],得到惠勒-德维特方程(Wheeler-DeWitt equation)。对于几乎是无穷多个自由度的宇宙来说,惠勒—德维特方程比较复杂,难以求解。常采用一些简化模型,对于均匀且各向同性的宇宙,选用具有很高对称性的小超空间模型(minisuperspace model),可得到描述量子宇宙的惠勒-德维特方程[11]
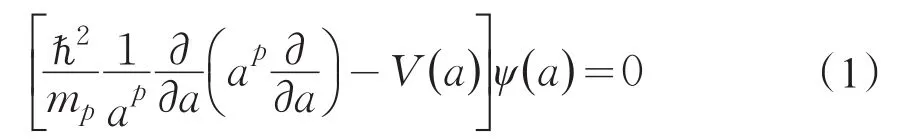
方程中ψ(a)是宇宙波函数,包含宇宙演化的所有信息,a为表征宇宙尺度大小的宇宙尺度因子,V(a)表示宇宙势函数,p为算符次序因子,mp表示普朗克质量。为了简便,在后文的计算中选择普朗克单位制,令ℏ=c=G=1。
2 宇宙波函数的动力学解释
宇宙波函数是复函数,因此可以将波函数写成

其中R(a)和S(a)都是实函数,可以得到宇宙波函数密度

量子力学中波函数密度表示粒子在空间的概率密度,即粒子在r附近处于体积为ΔV的空间内的概率p= | ψ(r)|2ΔV。对比量子力学,宇宙学波函数密度ρ(a)表示宇宙处于状态a的概率密度,那么(a) da表示宇宙处于a1至a2之间的概率。不同于量子力学,我们将这个概率解释为在整个宇宙的演化时间T内,宇宙从a1演化至a2所用的时间,用公式表示为

波函数的概率密度很小;表明宇宙处于a1至a2之间的时间很短,即宇宙膨胀(收缩)得很快。反之宇宙的概率密度大表明宇宙演化的慢,处于a1至a2之间的时间长。
从惠勒-德维特方程(1)出发容易得到系统的守恒流 ja以及守恒方程[12-13]

其中c0为积分常数,S'表示S(a)对尺度因子a的导数,由于宇宙尺度因子a以及R2都大于零,因此c0的符号与S'相反。
通过量子哈密顿-雅克比理论,可以得到尺度因子a的演化方程[14-15]

式(9)表明:当 S'>0时,a˙<0,即宇宙收缩;而当S'<0时,a˙>0,宇宙膨胀。
通过式(8)和式(9)可以得到
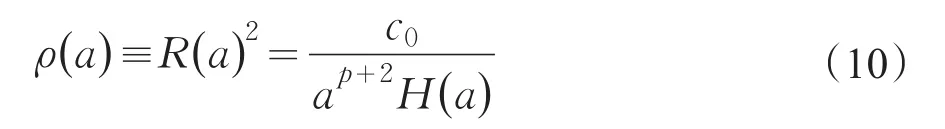
3 宇宙波函数动力学解释的应用
3.1 算符次序因子的确定
算符次序因子 p是惠勒-德维特方程中由于算符次序不确定引入参数,不同的取值对应不同的量子效应,因此它对早期宇宙的演化有重要影响,p如何取值仍未有定论。本文要求宇宙波函数处处收敛,即宇宙概率密度ρ()a在任何时候都是一个有限值,可以给出算符次序因子的约束。
现代宇宙论表明宇宙在极早时期(a→0)经历指数暴涨时期[16],这个阶段哈勃参数HIn是有限值且变化缓慢,根据式(10)
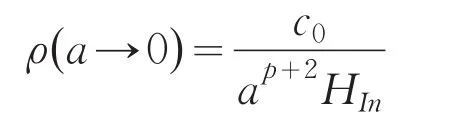
要求ρ(a →0)有限可以得到 p+2≤0。
另一方面,尺度因子a很大时,宇宙处于暗能量主导时期,此时宇宙指数膨胀,哈勃参数HDE为常数,同理根据式(10)可得
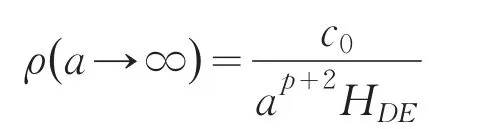
要求 ρ(a →∞ )有限,可以得到另一个边界条件p+2≥0。
因此,根据上述两个边界条件我们得到了算符次序因子的一个约束:p=-2。这个约束消除了惠勒-德威特方程中算符次序引起的不确定性。将p=-2代入式(10)得到

可以看出宇宙波函数密度仅与哈勃参数有关,即宇宙波函数密度只与宇宙膨胀或收缩的速度成反比。

图1 Hawking-Hartle给出的无边界波函数示意图
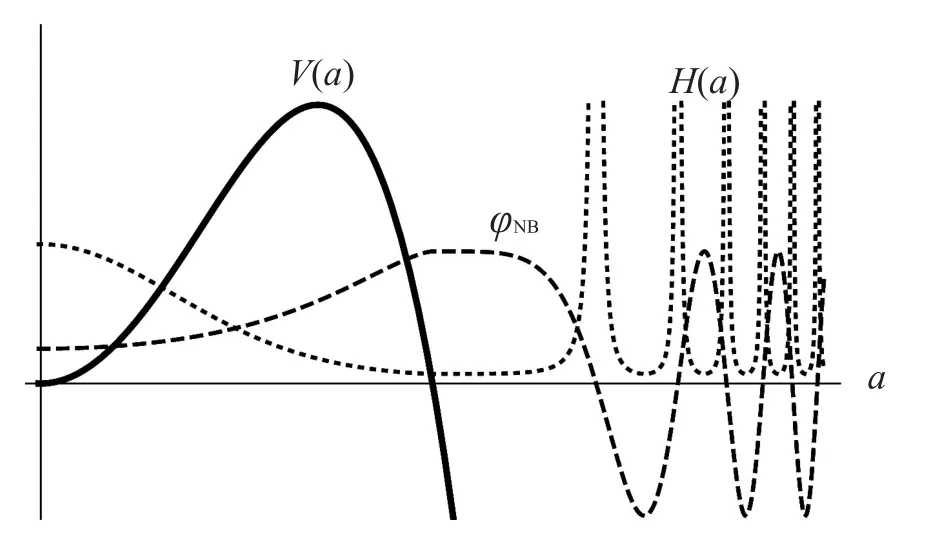
图2 无边界波函数给出的哈勃参数演化规律
3.2 宇宙波函数的选择
惠勒-德维特方程(10)为二阶微分方程,完全确定波函数需要合适的边界条件。目前有两种类型的宇宙波函数方案,一种是Hawking、Hartle根据欧氏空间的路径积分给出的无边界方案(no-boundary propose)[2],另一种是Vilenkin根据量子隧穿的思想得到的隧穿方案[3],这两种方案哪种正确仍存在争论[17-18]。我们将波函数的动力学解释应用于这两种方案,研究两种方案下宇宙的演化情况。
对于包含宇宙学常数Λ的封闭宇宙,宇宙的势函数可以写为

将式(12)代入惠勒-德维特方程(1),根据霍金和哈托给出了无边界波函数方法,可以得到宇宙波函数为

图1为无边界波函数示意图,图中实线为宇宙势能曲线,虚线为宇宙波函数。宇宙很小时(a2Λ≤1),宇宙处于量子时期。从图中可看出,在a=0时波函数ψNB为有限值,即量子宇宙中在a=0处无奇点。当宇宙很大时(a2Λ>1),宇宙波函数不断震荡,震荡的频率随着尺度因子a的增加而增加。此时波函数为纯实数,可以看做是时空膨胀态和收缩态波函数的叠加。根据波函数动力学解式(11)可以得到哈勃参数的演化规律,图2为根据无边界波函数得到的宇宙演化规律,图2中点线表示哈勃参数的演化情况,在宇宙很大时,哈勃参数在快速震荡,很显然这并不满足现在的观测结论。
在此模型下,宇宙势函数相当于一个势垒,量子力学中粒子穿过势垒后只有出射波。根据量子隧穿模型Vilenkin提出了隧穿边界条件,得到宇宙波函数为

图3和图4分别画出了隧穿模型下宇宙波函数和哈勃参数的演化规律。隧穿模型中,波函数只包含一支出射波(膨胀态波函数)。从图4可看出隧穿模型下,哈勃参数为常数,宇宙处于指数加速膨胀状态,这与现在的天文观测结果相一致。
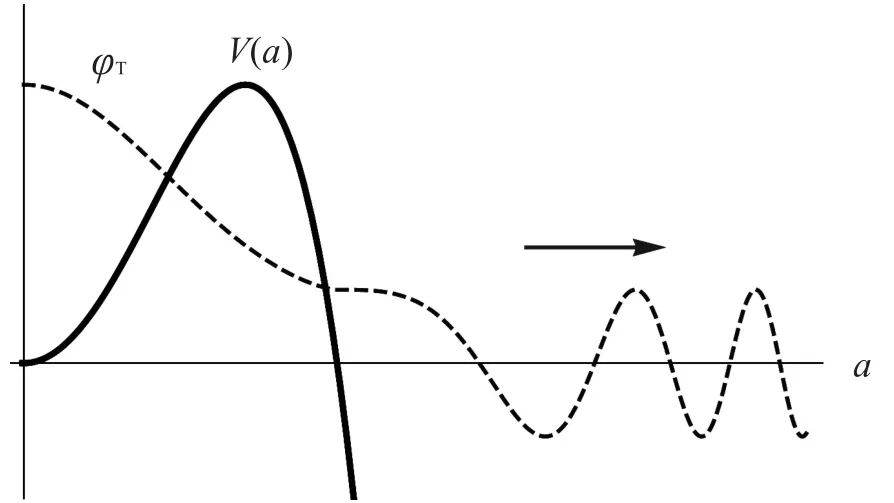
图3 Vilenkin给出的隧穿波函数示意图

图4 隧穿波函数给出的哈勃参数的演化规律
4 结论
本文提出了宇宙波函数的动力学解释。在此解释中,宇宙波函数的概率密度ρ(a) Δa 表示在整个宇宙演化的时间T内,宇宙处于Δa的概率,其正比于宇宙处于此状态的时间Δt。通过计算得到了宇宙波函数密度与哈勃参数之间的关系(式(10)),这样将宇宙波函数密度与可观测量哈勃参数联系起来。其次要求波函数密度收敛,得到了算符次序因子的约束条件。最后,将概率解释用于无边界波函数和隧穿模型波函数,计算表明隧穿模型波函数更能反映宇宙的演化规律。
