对一道高考模拟题的分析与思考

广东省广州市第六十六中学(510460) 王松岳

2018年广州一模测试题中的理科数学第20题代表近年来圆锥曲线问题的热点,值得去认真思考,并挖掘其中的来源.

一、原题再现

解读上面的解题过程,发现由一个定点T(4,0)出发的一组动直线,经过对称变换后,回归于定点G(1,0),估计这不是一个特例,猜想对于x轴任意一点都应该成立.

二、由特殊到一般

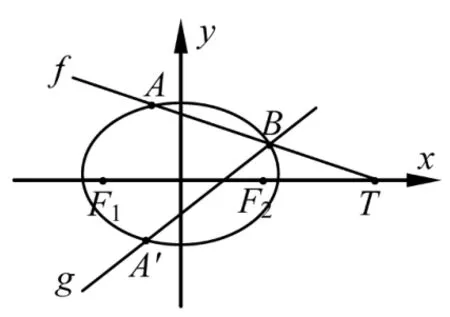
图1

三、把结论推广到其它圆锥曲线

对于抛物线也有类似的结论:

结论3过点T(n,0)(n̸=0)的直线l与抛物线C:y2=2px(p＞0)相交于点A(x1,y1),B(x2,y2),点A′(x1,−y1)与点A(x1,y1)关于x轴对称,则直线A′B恒过定点(−n,0).当n＞0时,应排除斜率不存在与斜率为零的直线.

四、追根溯源,命题背景分析

本题的命题背景来自于圆锥曲线的极点与极线.极点与极线问题是近年来高考的热点问题,此类问题越来越多出现在高考卷中,可以说已经成为高考解析几何大题的命题“新宠”.虽然不能够直接套用极点与极线的相关结论用于解答,但教师如果能够了解掌握相关理论,从更高的角度看对问题,对教学是有很大帮助的.下面给出极点与极线的定义,定理及相关性质.

定义1设两点P,Q的连线与圆锥曲线C相交于M1,M2,如果M1,M2被P,Q调和分割(即=−1,这里的线段均为有向线段),则称P,Q关于圆锥曲线C成调和共轭.

定义2如图2,P是不在圆锥曲线上的点,过P引两条割线依次交圆锥曲线于四点E,F,G,H,连接EH,FG交于N,连接EG,FH交于M,则直线MN为点P对应的极线.若P为圆锥曲线上的点,则过点P的切线即为极线.

定义3如图3,(极线方程公式)已知圆锥曲线C:Ax2+By2+2Dx+2Ey+F=0,则点P(x0,y0)与直线l:Ax0x+By0y+D(x0+x)+E(y0+y)+F=0是该圆锥曲线的一对极点和极线.

由上述极线方程公式可知,圆锥曲线对称轴上的点的极线垂直于该对称轴.

图2

图3

定理1一点P关于圆锥曲线C的所有调和共轭点的轨迹为一条直线l,称直线l为点P(关于圆锥曲线C)的极线,点P称为直线l(关于圆锥曲线C)的极点(简称极).

特别地,圆锥曲线焦点的极线就是与之对应的准线.当点P在圆锥曲线的外面时,其极线l是圆锥曲线C从点P所引两条切线的切点所确定的直线(即切点弦所在的直线).

定理2(配极原则)点P关于圆锥曲线C的极线l经过点Q⇔点Q关于圆锥曲线C的极线m经过点P;直线l关于圆锥曲线C的极点P在直线m上⇔直线m关于圆锥曲线C的极点Q在直线l上.

由定理2可知,共线点的极线必共点;共点线的极点必共线.

由上述结论可知,本次2018年广州一模理科数学第20题就是涉及极点P(n,0)关于椭圆的极线的问题.

五、高考链接

1.(2008年山东卷理科第22题)设抛物线方程为x2=2py(p＞0),M为直线y=−2p上任意一点,过点M引抛物线的切线,切点为A,B.

(1)求证:A,M,B三点的横坐标成等差数列;(2),(3)略.

2.(2010年江苏卷理科第18题)已知抛物线C的顶点为O(0,0),焦点为F(0,1).

(1)求抛物线C的方程;

(2)过点F作直线交抛物线C于A,B两点.若直线AO,BO分别交直线l:y=x−2于M,N两点,求|MN|的最小值.

3.(2015年全国I卷理科第20题)在直角坐标系xOy中,曲线与直线l:y=kx+a(a＞0)交于M,N两点.

(I)当k＞0时,求曲线C在M,N两点处的切线方程;

(II)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.

从近年来看,有着极点与极线背景的高考试题,越来越多地出现,如果教师能够高屋建瓴,加深对题源的认识,就能更好地把握试题,对教学提供很好的帮助.