社会成本问题讨论

2018-09-12危立

合作经济与科技 2018年20期

危立

[提要] 本文着重研究《社会成本问题》的事例部分，试图利用数学模型的视角，以数学恒等式、不等式对事实事例进行更系统直观的描述。试图找到一种模型，以及分析流程能够建立，以此能够概括以及统一各种事例的情况，使社会成本问题系统化，科斯定理体系化。而后，初步结合一些实际情况进行讨论，尝试对比税收模型，以及作出在社会发展问题上，国家、法律、政府规范、引导等作用的一些思考。

关键词：社会成本问题；数学模型；效益最大；政府引导

中图分类号：F0 文献标识码：A

收录日期：2018年5月8日

1960年10月，著名法律经济学家罗纳德·科斯的一篇名为《社会成本问题》的论文发表于《法律与经济学杂志》。这篇文章引起了学术界的广泛讨论与学术轰动，同时也是帮助科斯本人赢得诺贝尔经济学奖的代表之作。《社会成本问题》一文堪称现代产权理论权威之作，它成功地将法学与经济学结合在了一起，同时也从中应运而生了新制度经济学，以制度、法律、规则的眼光之下，应用经济学分析原理，阐述了在经济发展时期的社会问题，关于涉及到双方的发展经营有互相影响、相互冲突的时候，应该采用经济学中成本最小化、效率最大化的视角看待问题的观点。同时，在法律、福利与权利的相关问题上做出讨论。

《社会成本问题》的发表，同时带来了一个法律经济学上著名的定律——科斯定理的产生。然而罗纳德·科斯本人在论文中并未总结归纳而明确提出，这是之后的学者根据科斯在论文中所阐述的观点提炼而出。因此，科斯定律并没有标准的、权威的、固定的语言描述。科斯通过在论文中论述不同事例的不同情况，来阐述核心思想，他写道：“But the ultimate result（which maximizes the value of production）is independent of the legal position if the pricing system is assumed to work without cost。”概括来说，作者认为，科斯定理在通过实例讨论之下，可以理解为：当双方的经济发展出现一方对另一方有产生损害影响而法律没有明确界定的时候，如果交易成本较低甚至没有，权利会发生重组，最后稳定在资源配置最优与效率最大的方案之上。论文批判了传统看待有害影响的视角，以减少矛盾，惩罚损害者的角度实际上并不是最优的解决方法。科斯定理首先想表达的就是在较理想的社会与市场之下，哪一方能发挥出物品或生产要素的最大效益，哪一方就拥有权利。

科斯的论文主要以文字叙述为主，本文着重研究《社会成本问题》的事例部分，试图利用数学模型的视角，对科斯论文中的实例加以更系统直观的描述。同时，本文试图找到一种模型能够建立，以此能够概括以及统一各种事例的情况，使社会成本问题系统化、科斯定理体系化。而后，本文初步结合一些实际情况进行进一步讨论，尝试对比税收模型，以及讨论在社会发展问题上，国家、法律、政府规范、引导等作用的一些思考。

接下来，本文会着重研究讨论科斯论文中的实例部分，以建立数学不等式、恒等式与寻找模型的视角进行问题的重新描述与论证。

一、农夫与养牛者的简单例子证明与讨论

《社会成本问题》通过实例，阐述问题的切入点在于农夫与养牛者的简单例子。养牛者与农夫各自的土地相互邻接，牛会对庄稼产生损害，看待这一问题时，我们不能只着眼于如何防止牛踩踏庄稼，如何惩罚养牛者使他不再养牛，限制了养牛同时也是对养牛者的一种损害，是要牛还是要庄稼？我们应当看到，当农夫和养牛者能够交流并达成某种交易，可以达到双赢的局面。

农夫与养牛者的例子，讨论依赖于科斯论文中给出的数据。本文也依旧使用并基于表1数据，求解讨论。（表1）

可以发现，牛的数量与谷物每年损失量是非线性的，与每增加一头牛而增加的谷物损失，即谷物对牛数目的边际损失是线性相关的。文中已假定谷物单位价格每吨1元，所以按照：总价值=单价×吨数的公式，单价为1，则损失价值即损失谷物吨数。

设牛群数目：x头；谷物年损失：Y元；每增加一头牛而增加的谷物损失：y；假定牛群对谷物损失趋势不变，则利用数据拟合得到关系函数：Y=x2+x；y=x；函数Y（x）图像如图1所示。（图1）

可以看出，牛群的扩大对于谷物损害为二次方多项式增长，农夫与养牛者达成的交易一定不是农夫的单方面退让也不会是养牛者无止境的赔偿，而是会存在上界并有最优点。拟合图像在本文接下里的讨论中还会使用到。

对符号进行假设说明，如表2所示。（表2）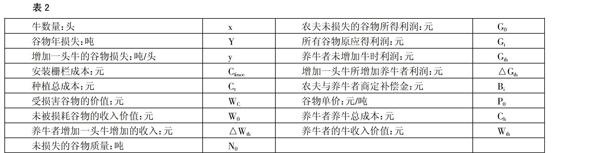

（一）養牛者对庄稼损害负责。养牛者养的牛会对庄稼造成损害，但是损害未必要让养牛者全部承担，那样，不仅挫伤养牛者积极性，当赔偿超越利润的时候，甚至会使得养牛者退出市场，使得市场损失一种产品。此时我们要看，只要二者商定补偿，既让农夫得到高于被损害后利润的收入，又让养牛者不至于继续亏本，则方案是双赢的。

对养牛者来说：扩大牛群的条件：△Wth≥P0·y，养牛者也可建栅栏，假定建栅栏成本：Cfence=9元，养牛者考虑是否建栅栏，即考虑利润最大：

MAX{Gth=Wth-Cfence，Gth=Wth-P0·y}

情形1：没有养牛者时，土地耕种。在农夫的计算中：W0=N0·P0Wt=Wc+W0Gt=Wt-CtG0=Gt-Wc，当Wt-Ct>0时，农夫种植获利，而Wt-Ct≤0时，农夫选择不种植。而损失发生时，当损失的利润不能为正数时，农夫也会选择不耕种。G0=Gt-Wc≤0带入表达式，可得到：W0-Ct≤0，即获利与否取决于谷物损失价值。农夫与养牛者达成交易后，可知双方的计算：Gth+△Gth-B>0Gt+B>0时，二者皆有利可图。

讨论农产品市场接近的完全竞争市场，单个农夫不会随意扩大和缩小供给，因为单个买卖者无法改变市场均衡，只会使得单个买卖者利润减少，如果B与市场价合适，则农夫有所补偿，会减少产量。

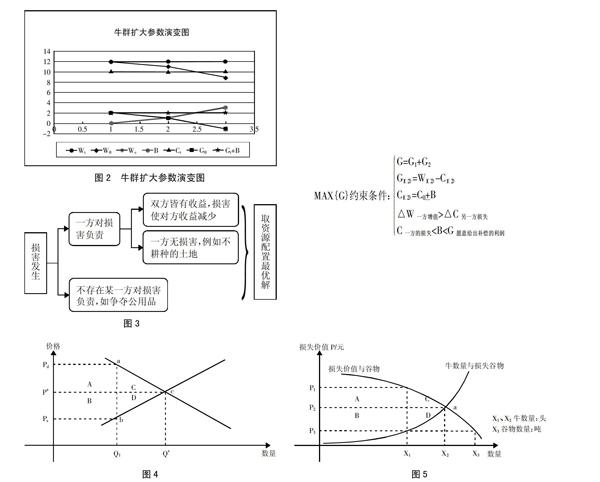
当牛群扩大，演变如图2，农夫若同意停止耕种，或者部分停止耕种，也可获利。可知，牛群的增加可以减少土地耕种。

情形2：没有养牛者时，土地不耕种。此种情形常常发生于狭长地带，牛群必经之地，耕种也没有意义，同时伴随着耕种成本大于收益价值：Wt-Ct<0，此时，就算没有牛群，农夫也不会进行耕种，对双方的计算：B>0，0

（二）养牛者对庄稼损害负责。若养牛者无需进行负责，则是农夫给养牛者一定数额的金钱让其减少牛的数量，其实就是减少自己的损失，这种情况虽然有悖于日常认知，但是谷物的损失也可视作成本，在完全竞争市场中，边际成本=边际收益=价格，所以交易达成，长期均衡并不会影响。

二、四个典型事例的关系描述及统一模型

（一）庫克诉福布斯案。草席厂受到制造厂的空气污染，是要草席厂安全生产限制制造厂制造，还是要草席厂搬走？

G总=G草+G制G草=W草-C原-C受影响+BG制=W制-C原-C受惩罚，想要利润最大，则看哪一方创造的价值最大，而受到影响后的利润可以抵消并超过对方的利润，在达成协议后，是否能使得社会生产总利润最优即求：MAX{G总}。

（二）斯特奇斯诉布里奇案。医生因为糖果商的机器噪音无法正常诊疗。法院的判决可以决定谁拥有权利。若医生胜诉，达成最优条件：B>C医生迁移或医生损失，而实质于：△W糖果商增加收入>△C医生收入的减少。若糖果商胜诉，情况则是医生要付给糖果商B，让糖果商减少机器，则：C糖果商减少机器带来损失

（三）布莱恩特诉勒菲弗案。这是典型的烟尘妨碍问题，高处的房子导致矮处的房子的烟囱发生倒吸现象，而权利的认定又不是十分清晰。在矮处房子的人认为高处房子侵害自己排出烟气的权利，而高处房子的角度看，倒吸是因为矮处房子的人自己排放烟气所引起的。此案的不同在于，双方都引起了损害，互相损害的发生，则不是单方面进行赔偿的问题了。

（四）巴斯诉格雷戈里案。此案双方因为公寓使用问题而产生纠纷，双方都存在自己的合法权益，纠纷的焦点在于空气的使用。显然，空气作为公共品，双发皆在于使用而不存在归属。此时要考虑的就是哪一方更愿意付出补偿，使得己方愿意且对方满意。此时，加总的价值，甚至可以说是加总的辛福度得到了全面的提高。

四桩具体案例，虽法院各有判决，但总体来说，按照使用最优者享有权利的解决方法并无太大改变。考虑本文所列举的问题，首先要进行情况的判断。图3是对问题类型的概括，也是一种考虑问题的路径。（图3）