基于GIS的AHP区间铁路线路方案比选研究
2018-09-11谭衢霖秦晓春
李 然,谭衢霖, ,白 雁,秦晓春,
(1.北京交通大学 土木建筑工程学院, 北京 100044;2.北京交通大学 线路工程空间信息研究所, 北京 100044)
铁路选线设计是一个多因素、多层次的复杂系统工程。在选线过程中,首先根据影响因素和已知条件选定若干个可行的线路方案,然后根据相应的指标值对可行方案进行多目标评价选取[1]。在铁路线路评价中,影响方案评选因素非常复杂,既有定量指标,又有定性描述,既有客观条件,也有主观偏好,而且各个因素相互关联。尽管已有多种多目标评价选取方法,但是,很难用一种单一的方法很好地解决铁路选线方案多目标综合评价问题。近年来,为了综合多种因素进行铁路线路评价,研究者们开始注意到地理信息系统技术优势[2]。王明生,于金金等[3]将GIS的空间分析功能应用于铁路选线方案综合影响评价领域,将原来的定性描述的指标进行定量描述。宁锐等[4]提出了基于RS(遥感)、GIS(地理信息系统)的铁路选线设计影响因素分析提取模型。张晓东等[5]从理论模型角度出发,提出了铁路选线设计影响因素信息分析提取模型及定线方案综合分析评价模型。本文综合了坡度、坡向、土地利用、植物群落、水域和湿地、道路、文物古迹和建筑用地8个影响因素作为多目标决策的单成本因素,建立了基于地理信息系统(GIS)的层次分析法(AHP)线路方案比选模型,对辽宁省康平站—法库站区间铁路线路方案进行多目标评价分析。
1 GIS空间分析方法
1.1 多环缓冲区分析
在GIS中,缓冲区分析技术是确定地物周围影响范围或服务范围的重要空间分析方法[6]。缓冲区是指在地物周围创建一个具有一定宽度的多边形,这个多边形区域就是缓冲区。在GIS中,所有研究对象的缓冲区都是多边形,而且创建的缓冲区会构成一个新的面数据图层。由于GIS数据分矢量数据与栅格数据,所以缓冲区也分为矢量缓冲区和栅格缓冲区。矢量缓冲区分为点缓冲区、线缓冲区和面缓冲区。点缓冲区是以点为中心的一个圆形区域;线缓冲区是向线的一侧或两侧平行扩展形成的一个区域;面缓冲区是面状要素向里或向外扩充的区域。栅格缓冲区是像元向东、南、西、北、东南、西南、西北、东北8个方向以一定距离扩展形成的区域,像元与东、南、西、北4个方向的相邻像元的距离为L,与东南、西南、西北、东北4个方向的相邻像元的距离为
多环缓冲区则是在输入要素的周围以指定的距离创建多个缓冲区。这样就可以确定地物对不同距离的周围空间造成影响程度。基于多换缓冲区技术可以把指标层因素成本值取1、3、5、7、9储存在环形缓冲区域内,表示在该区域内布线成本的高低,即值越高表示在此像元内布线综合成本越高;值越低表示在此像元内布线综合成本越低。缓冲区示意图,如图1所示。

图1 缓冲区示意图
1.2 空间叠加分析
空间叠加技术就是将所需的空间要素与多个数据图层进行叠加,产生一个新要素图层[7]。该新要素图层即为将多个图层的属性数据指定给所需的空间要素上。根据GIS数据结构的不同,可分为矢量数据的空间叠加和栅格数据空间叠加。点与面(线)空间叠加就是根据矢量数据层中点要素与另一矢量数据层中的面(线)要素的空间关系(相离、相交、包含等)确定点要素的空间数据与属性数据。线与面空间叠加就是通过线要素与面的空间关系,确定线要素的空间属性数据。面(线/点)与面(线/点)的空间叠加就是根据空间关系将两个或多个面(线/点)矢量数据叠加,生成一个新的面(线/点)数据层,新生成的面(线/点)数据具有原数据的共同属性特征。 栅格数据的空间叠加是指在栅格叠加中,每个图层的每个像元都引用相同的地理位置,这使各图层的栅格的属性值通过代数运算(加、减、乘、除等)和逻辑运算(与、或、非、异等)合并到一个图层中,这个过程即为栅格数据的空间叠加。
2 层次分析法
2.1 递阶层次结构模型建立
线路评价递阶层次结构模型包括目标层,准则层,指标层和方案层[8]。目标层即为获取最优方案。准则层为地形、地物和环境综合因素[9]。指标层即为坡度、坡向、土地利用、植物群落、水域和湿地、道路、文物古迹和建筑用地。方案层为可供选择的选线方案。递阶层次结构模型,如图2所示。
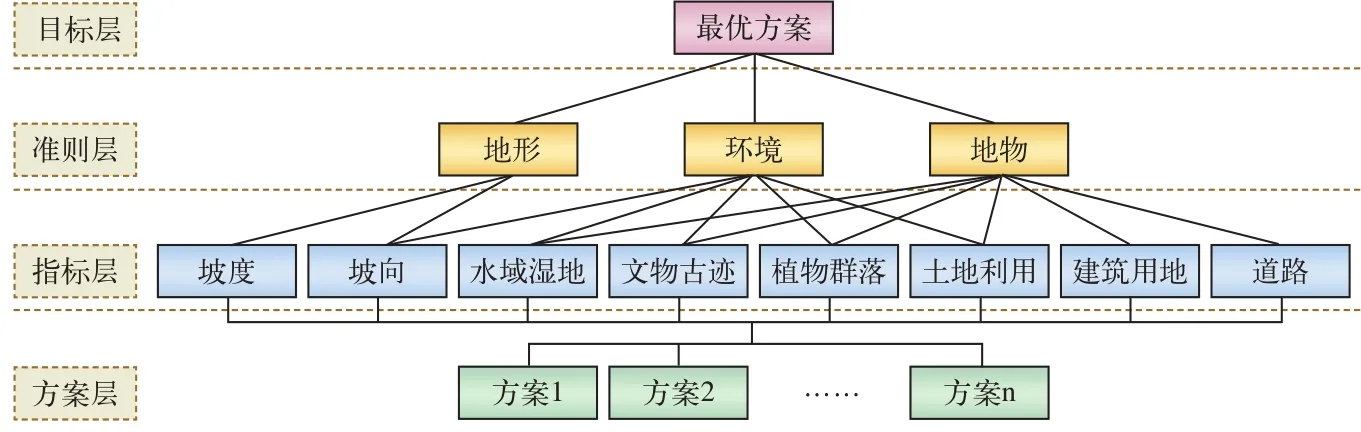
图2 层次分析法递阶层次结构图
2.2 指标层赋值及权重确定
(1)构造判断矩阵。判断矩阵反应指标层对准则层(准则层对目标层)的相对重要性。判断矩阵的取值为相应两元素对上层的影响比。采用T.L.Saaty提出的1~9比例标度,如表1所示。

式中, λmax—判断矩阵中唯一的最大特征值;

表1 1~9比例标度
A—分层次的判断矩阵;
W—权重向量(特征向量),其分量全是正向量。
将得到的权重向量(特征向量)作归一化处理即可得到各因素(指标)相对于上一层的权重值。
(3)进行一致性检验。CI为度量判断矩阵偏离一致性的指标,则有:
我们将新生代农民工积极主动的参与教育培训的过程定义为“个体主动赋权”,同时将国家、社会与企业等主体为新生代农民工教育培训提供资源的行为定义为“外力推动赋权”。从推动教育培训有效发展的角度来讲,新生代农民工个体主动参与教育培训与国家、社会和企业的外力推动都是必不可少的。如果缺乏外力推动,新生代农民工将缺乏有利的参加教育的制度环境,他们将在参加教育培训的过程将遭遇更多的无力感;若缺少新生代农民工个体的主动参与,那么针对新生代农民工群体的教育培训没有实质性的意义。

RI为平均随机一致性指标,通过表2查到。

表2 平均随机一致性指标RI
CR为矩阵一致性检验指标,则有:
CR=CI/RI
当CR<0.1时,判断矩阵一致性符合要求,否则,需要对判断矩阵进行适当的调整和修改,直到结果符合我们的要求为止。
3 康平—法库线路方案比选
3.1 康平—法库线路比选方案
康平与法库直线距离约为20 km。现根据纸上选线方法,确定了两套比选方案,方案1(线路1)与方案2(线路2),如图3所示。
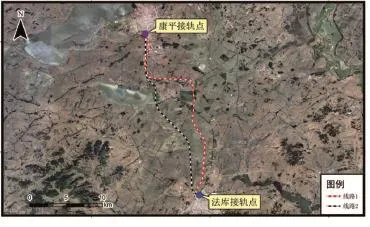
图3 区间铁路线路方案图
3.2 指标层成本因素的赋值及权重确定
(1)水域和湿地按缓冲区进行赋值。在接近水域和湿地地段施工,对水域和湿地造成破坏大,同时产生的工程费用高。因此越接近水域和湿地,成本值越高。水域和湿地本身成本值取9;0~50 m缓冲区成本值取7;50~100 m缓冲区成本值取5;100~200 m缓冲区成本值取3;>200 m缓冲区成本值取1。
(2)植物群落按生态敏感性的高低进行赋值[10]。在受到外界干扰时,生态敏感性越高的植物群落,越容易产生生态环境问题。因此生态敏感性越高,成本值越高。杉木林、加杨林、枫杨林、板栗林等成本值取9;紫叶李林、桂花林、马尾松林等成本值取7;灌丛、油茶、林竹林等成本值取5;水生植物、旱作植被、水稻等成本值取3;无植物、忙草地、荒草地等成本值取1。
(3)坡度按坡度大小进行赋值。坡度越大,工程费用越高,成本值越高。>20°成本值取9;15°~20°成本值取7;10°~15°成本值取5;5°~10°成本值取3;0°~5°成本值取1。
(4)文物古迹按缓冲区进行赋值,在接近文物古迹等敏感地区修建铁路,无论是施工还是运营阶段,都会对其产生影响。因此越接近文物古迹等敏感地区,成本值越高。0~200 m缓冲区成本值取9;200~300 m缓冲区成本值取7;300~350 m缓冲区成本值取5;350~400 m缓冲区成本值取3;>400 m缓冲区成本值取1。
(5)土地利用按其对生态平衡的不同作用及对施工干扰程度赋值,沟渠、河流、湿地、滩涂、坑塘等成本值取9;林地、果园、灌木林地等成本值取7;水浇地、水田、旱地等成本值取5;草地、农村宅基地等成本值取3;公路用地、农村道路、工业用地等成本值取1。
(6)道路按缓冲区进行赋值。越接近道路,相互影响越严重。因此越接近道路,成本值越高。道路本身成本值取9;0~10 m缓冲区成本值取7;10~20 m缓冲区成本值取5;20~50 m缓冲区成本值取3;>50 m缓冲区成本值取1。
(7)建筑用地按缓冲区进行赋值,越接近建筑,视觉噪声等干扰越严重。因此越接近建筑,成本值越高。建筑本身成本值取9;0~20 m缓冲区成本值取7;20~40 m缓冲区成本值取5;40~60 m缓冲区成本值取3;>60 m缓冲区成本值取1。
(8)坡向按植被光照情况进行赋值,东南-西南成本值取9;东–东北成本值取7;北成本值取5;西-西北成本值取3;平面成本值取1。
邀请5位相关专家对8个成本因子中的每两两因子相对重要性做出评价,计算得出各个评价因子的权重值,并经一致性检验确定其可以作为评价的权重使用。由此方法,本文最终确定水域和湿地、植物群落、坡度、文物古迹、土地利用、道路、建筑用地和坡向8个成本因子的权重值分别为0.235、0.225、0.165、0.135、0.1、0.065、0.05、0.025。成本因素的分级、赋值与权重,如表3所示。
3.3 空间叠加及多方案综合评价
根据拟定方案的线路等级,路基宽度不超过8 m,利用GIS软件的“缓冲区分析技术”,建立铁路线路两侧4 m的带状缓冲区,如图4所示。

图4 线路方案1与方案2的缓冲区
单位面积总成本数学模型为:

其中,i为方案编号;j为区域编号;k为成本因素分级赋值的编号;n为成本因素总数;Cij为方案i第j个区域的单位面积总成本;Sij(k)为方案i第j个区域的成本因素k分级赋值;W(k)为成本因素k的权重,为第i个分级赋值单元的第k个成本因素的综合值。
利用GIS软件的空间叠加技术,分别将方案1和2,与8个因素分级赋值图层进行空间叠加,得到叠加后方案1和叠加后方案2,如图5所示。方案i

表3 成本因素的分级、赋值与权重
总成本数学模型为:

其中,i为方案编号;j为区域编号;mi为方案i区域总数;Mi为方案i总成本;Cij为方案i第j个区域的单位面积总成本;Aij为方案i第j个区域的面积。
方案1与方案2的总成本,如表4所示。方案2

图5 线路与各成本因素空间综合叠加图
总成本<方案1总成本,方案2优于方案1。

表4 方案总成本
4 方案比选结果
方案2与方案1相比,方案2线路穿越区域地势较平坦,远离了陡坡、沟坎,施工难度较低,安全系数较高;远离湿地和水域,减小了对湿地和水域的影响,保护了水域和湿地,同时减少工程数量,降低综合成本;远离生态敏感性高的植物群落的地区,保护了生态系统;通过草地、旱地等易于改造成铁路的地区,远离施工程度难,及对生态平衡有重要作用的土地利用地块;选择对植被群落光照影响少的坡向,对生态系统具有深远的意义;与道路保持一定的距离,互不干扰;与文物古迹保持一定的距离,对历史文物具有保护作用;与其他建筑保持了一定距离,避免了视觉干扰。由上分析可知,方案2优于方案1。
5 结束语
基于GIS的AHP线路方案比选模型对于生态环境保护、提高工程安全性、降低工程造价具有重要作用。本文以辽宁省康平站—法库站区间铁路为例进行方案比选,进而比选出了最优线路方案,为铁路线路方案决策部门提供了科学依据。
