灰色理论在铁路客运量预测中的分析研究

吴华稳

（国家铁路局 信息中心，北京 100891）

铁路客运量作为铁路客运市场体系中的重要指标，反映铁路运输生产成果以及铁路客运发展水平，体现着运输业为国民经济服务的情况，是铁路客运的晴雨表与风向标。鉴于铁路客运量和国家经济及企业发展联系紧密，铁路客运需求预测成为铁路供需和经济发展关系研究中一个重要问题，具有较强的实际意义和理论意义[1]。利用铁路客运量统计数据可以进行铁路建设项目经济评价、客运市场分析、监测、预测等，为运输组织、生产决策提供重要的基础数据。

铁路客运量受多因素、多层次的影响[2]。为了准确预测铁路客运量，需要收集大量历史数据，考虑到运量数据受季节、政策等多方面的影响，不确定性较强，从而导致难以建立准确的数学模型，有时即使数学模型能够建立，往往也会因缺乏足够的信息而不能估计模型参数，致使无法准确进行预测。本文依据灰色系统理论的特性，不涉及系统复杂的相互关系，只注重系统本身的白色信息，寻找系统自身的内在规律[3]。根据这个原理，在铁路客运量预测过程中，在对实际的历史数据分析的基础上，建立铁路客运量灰色预测模型，并进行残差校验，进而得到一系列的有价值的预测结果。

1 铁路客运量预测方法

1.1 定性预测方法

定性预测方法是主要以预测人员的经验判断为依据而进行的预测[4]。预测者根据自己掌握的实际情况、政策制度、实践经验、专业水平，对未来铁路客运量发展前景的性质、方向和程度做出判断。

定性预测方法：经济调查法、德尔菲法（专家调查法）、类推法（时间类推和局部类推）、头脑风暴法等。但这种方法往往在很大程度上取决于参加预测的人员的经验、专业理论水平以及所掌握的实际情况，因此存在片面性，准确性不高的缺点[5]。

1.2 定量预测方法

定量预测方法是以历史统计资料和有关信息为依据，运用各种数学方法来预测未来客运市场需求情况，即未来的运量。定量预测方法最大的优点就是客观性，这类方法的预测精度和可靠性在很大程度上取决于数据的准确性和预测方法的科学性。

定量预测方法：时间序列法（移动平均法、指数平滑法、自回归分析、趋势外推法、分形预测法、灰色预测法、ARIMA模型法）、非线性预测方法（混沌预测法、神经理论预测法、遗传算法理论）、影响因素分析法（马尔科夫法、回归分析法、系数法：乘车系数和产值系数）、组合分析法、四阶段法（交通生成、交通分布、交通方式划分）[6]。

2 理论分析及模型建立

2.1 无偏GM(1,1)

2.1.1 数据检验与处理[7]

假定，给定了原始时间序列X(0)：

使得新序列Y(0)={Y(0)(1), Y(0)(2), Y(0)(3), …, Y(0)(n)}的级比满足条件：

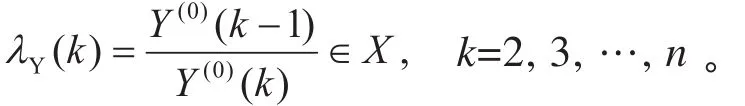
2.1.2 构造1-AGO序列

即对原始序列进行一次累加生成新的序列（如果原始序列不能满足级比条件，则对调整后的新序列Y(0)(k)进行变换）。

构造新序列为：

X(1)={X(1)(1), X(1)(2), X(1)(3), …, X(1)(n)}，其中：

2.1.3 构造紧邻均值序列

均值序列，即依一次累加原始时间序列的一次相邻项的移动平均[8-9]：

其中，Z(1)(k)=0.5X(1)(k)+0.5X(1)(k–1), k=1, 2, …, n。

2.1.5 求解传统灰色系数

采用最小二乘法求解灰色系数，记：

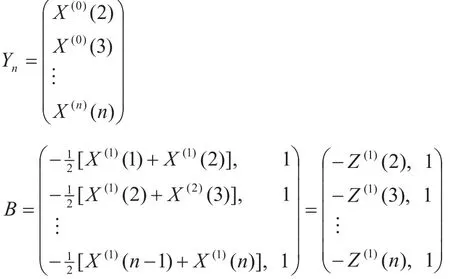
则可计算传统灰色系数：

2.1.6 建立无偏灰色预测模型

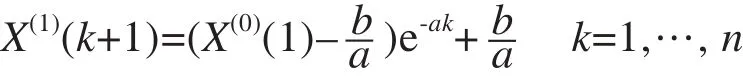
2.2 灰色预测模型的检验

计算原始序列X(0)和预测序列(0)的绝对残差序列 Δ(0)={Δ(0)(i), i=1, 2, …, n},Δ(0)(i)=|X(0)(i)–(0)(i)|，及相对残差序列 Φ={Φi, i=1, 2, …, n}，其中，并计算平均相对残差给定 γ = 0.01，0.05，0.1，如果满足＜γ且 Φn＜γ成立时，称模型为残差合格模型，且模型的检验结果分别为优、合格、勉强合格[10-11]。

3 无偏灰色理论在铁路客运量中的预测研究

现以1997—2016年20年间铁路客运量为基础数据，进行铁路客运量预测，预测年份为2017—2020年铁路客运量数据。如下通过无偏灰色理论进行预测。

（1）数据检验与处理。对铁路客运量20年的数据进行检验与预处理，通过1-AGO运算，得到累加数据序列X(1)(k)，结果如表1所示。

表1 1997—2016年铁路客运量数据 单位：万人

（2）对X(1)作紧临均值生成，令：Z(1)(k)=0.5x(1)(k)+0.5x(1)(k–1)， k=2, 3, …, 20，得 Z(1)=(Z(1)(1), Z(1)(2),…, Z(1)(20))，结果如表2所示。

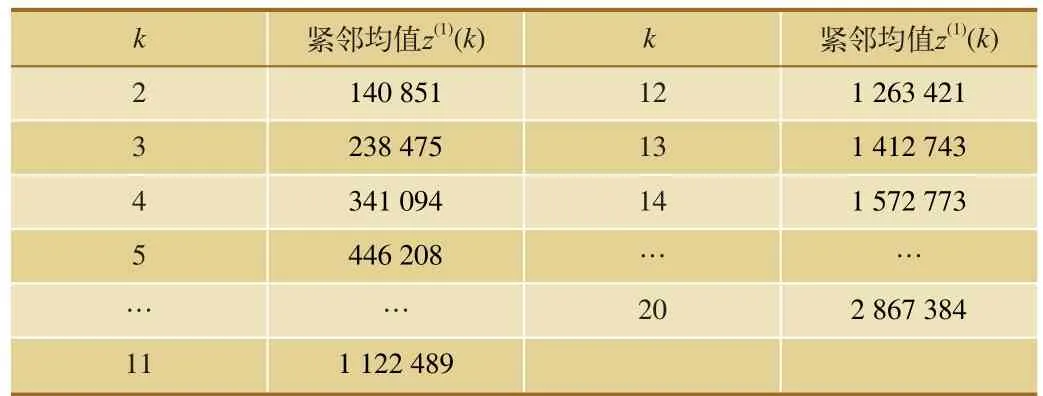
表2 铁路客运量X(1)(k)的紧临均值生成

（3）对参数a、b进行最小二乘估计，得：

（4）确定模型。无偏灰色铁路客运量预测模型：

（5）检验误差。通过上述无偏灰色铁路客运量预测公式并经过残差调整，计算1997—2016年铁路客运量预测值、残差Φ和相对误差，与BP神经网络预测结果进行对比，如表3所示。

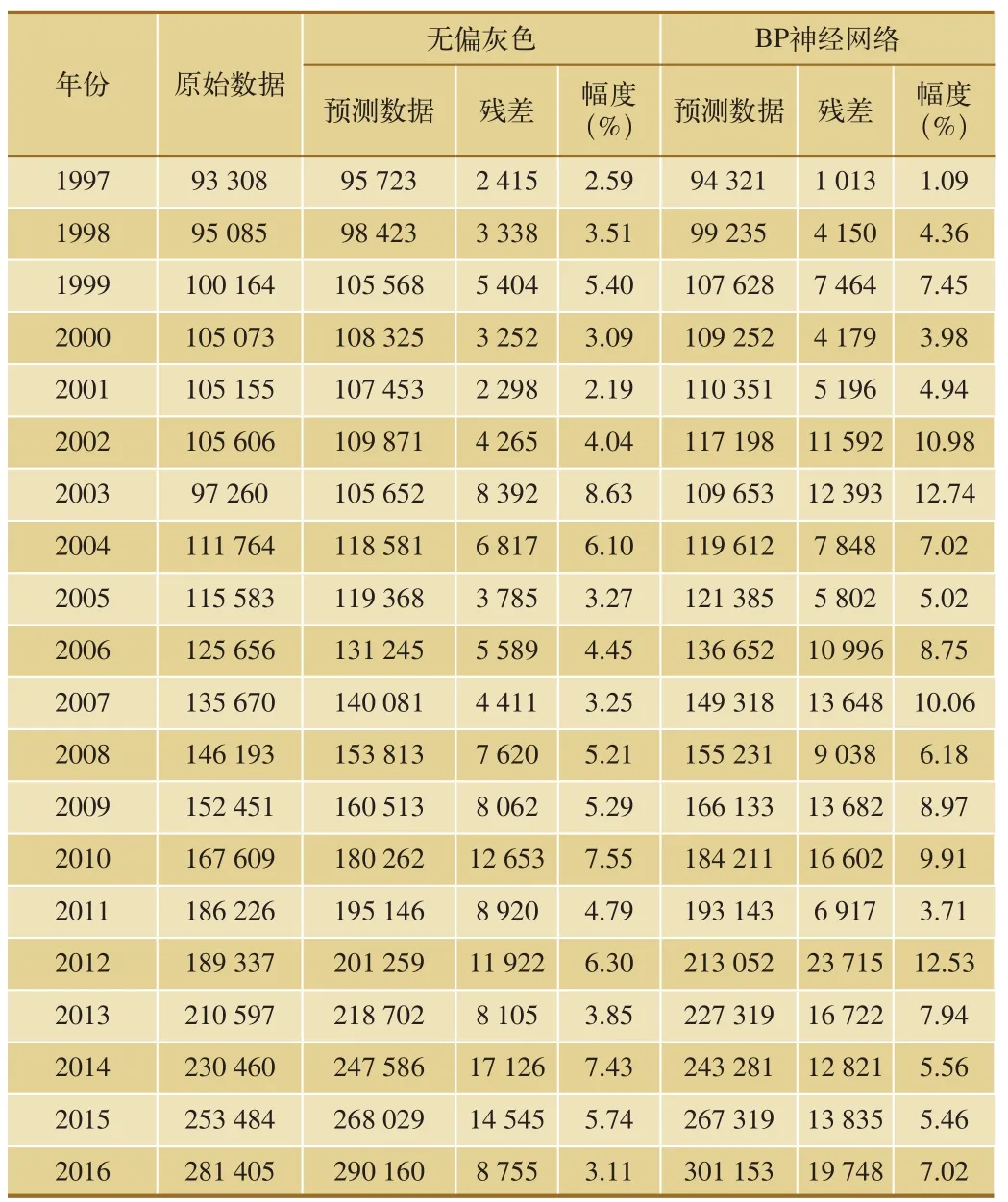
表3 1997—2016年铁路客运量预测数据 单位：万人

无偏灰色铁路客运量最小残差为2.59%，最大残差为8.63%，平均预测残差为= 4.79%，平均残差范围小于5%，通过残差检验。说明构建的铁路客运量预测模型可以容许并接受，可进行预测。

BP神经网络预测客运量最小残差为1.09%，最大残差为12.53%，平均预测残差为= 7.18%，BP神经网络平均预测残差7.18%远大于无偏灰色平均预测残差4.79%，因此，基于无偏灰色理论的预测方法对铁路客运量进行预测精度更高。

（6）“十三五”铁路客运量预测。通过构建的无偏灰色铁路客运量预测模型，对2017—2020年4年间铁路客运量数据预测，如表4所示，进而得到“十三五”期间铁路客运量预测数据。

4 结束语

本文以1997—2016年铁路客运量为基础数据，应用灰色理论预测方法，对铁路“十三五”时期的数据进行预测并对结果进行校验，经对比，其预测精度明显高于传统的BP神经网络预测模型，能够较为准确地预测铁路客运量。

表4 2017—2020年铁路客运量预测数据 单位：万人

在宏观趋势预测方面，本文应用了无偏灰色预测模型，一定程度上消除了传统灰色模型本身所固有的灰色偏差。在微观波动预测方面，无偏灰色模型较传统灰色模型更具有抗干扰性。因此无偏灰色预测方法在宏观预测以及微观预测方面均优于传统灰色模型。

在数据预测过程中，合理兼顾定性分析与定量计算对铁路客运量预测并非易事，下一阶段，将研究灰色理论与其他理论结合的组合预测模型；并进一步研究历史数据不全或精度不高的预测模型。