基于出行链的城际铁路站点选址双层目标模型

江欣国， 赵阳阳， 夏 亮， 章国鹏， 姬生飞

(1.西南交通大学 交通运输与物流学院，四川 成都 611756；2.长安大学 公路学院，陕西 西安 710064)

城际铁路作为一种具有大容量、快速、安全环保等优点的骨干运输方式，依据其服务范围，可划分为两大类[1]：区域城际铁路主轴系统(服务于城市群区域主要中心城市之间，以开行城际列车为主的干线客运专线，一般为100～300 km)和大城市城际铁路通勤系统(以承担大城市通勤客流为主，一般小于100 km).

城际铁路站点选址是城际线网规划的重要组成部分.合理的站点选址可减少工程投资，降低运营成本，方便旅客出行；否则易造成投资浪费，旅客出行不便，客流吸引效果差等问题，因此有必要对站点选址进行充分研究.

目前关于城际铁路站点选址包括以下两类：对无限多备选站点进行求解，在此基础上选择评价指标对选址方案进行优化，称之为连续型车站选址；在备选站点已知条件下的评价优化选址，称之为离散型车站选址.关于此类问题的研究，蒲浩等[2-3]先后通过“加权模板转换法”、“约束条件法”，选取投资成本、线站耦合程度等评价指标，采用“站点综合效益”进行铁路站址寻优；Lai等[4]采用“线站协同优化法”，建立基于投资成本、旅客出行费用等多目标选址模型；Samanta等[5]运用遗传和蚁群算法，以“综合费用最小”进行选址优化.目前连续型车站选址重点研究线路、车站、环境之间的相互约束，在此基础上选取评价指标进行优化，而忽略了城际站点收益及城际旅客市内出行广义费用等因素的影响.离散型选址则是在备选站点已知条件下的评价优化选址.

而对于离散选址问题，廖勇[6]将三角模糊数与TOPSIS法结合进行选址方案的综合评价，张天伟等[7]考虑非强制性定性、强制性定性和定量因素，建立车站选址0—1规划模型，潘玲巧等[8]通过构建方案层、因素层和指标层3层评价指标体系对车站选址进行综合评价，3种方法均对结果的客观性有一定影响；冯树民等[9]采用定量计算，建立“居民步行总距离最小”的选址模型，引入灰色聚类方法对相关指标进行取值，并未考虑相关的投资成本；王南等[10]将投资成本考虑在内，建立旅客出行和站点投资总费用最小的站点选址优化模型，但忽略收益因素对选址的影响；针对收益因素，刘强东等[11]将站点客、货吸引量纳入站点布设影响因素符合实际情况，建立社会综合效益最大的选址模型，运用遗传模拟退火算法进行求解，但对城市内部路网形态与客、货吸引量的相互关系考虑不足.目前离散型站点选址主要通过确定更完善的评价指标进行比选优化，但忽略城市内部路网形态，简化旅客市内出行广义费用的计算会对站点选址结果产生一定的影响.

针对以上问题，本文采用离散型选址模型，充分考虑市内交通对旅客城际间出行方式选择的影响，根据旅客起终点间的路网形态对其出行广义费用进行细化处理，提出一种基于出行链的城际铁路站点选址双层目标模型，并运用改进离散粒子群优化算法进行求解，从而提供一种从城际铁路运营者及旅客的角度优化城际站点布局的方法.

1 基于旅客出行链的客流分担率

1.1 城际旅客出行链

出行链可定义为由一系列驻点(停留某处进行活动的地点)和路段构成的出行集合[12].城际旅客出行链如图1所示.

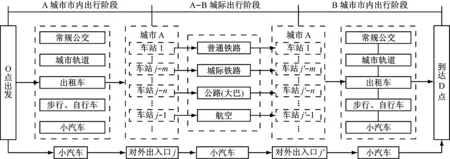
图1 城际旅客出行链

城际旅客出行链可分为3个阶段: I阶段：从城市A的出行链起点O (交通小区i)出发，经市内交通方式k，到达对外结点j；II阶段，从对外结点j，经城际交通方式α(j,j′)到达城市B对外结点j′；III阶段，从对外结点j′，经市内交通方式k′到达目的地D (交通小区i′).

1.2 广义费用函数

运输方式的服务特性决定旅客的广义出行费用，从而影响旅客的出行选择行为.本文市内出行考虑经济性、快速性、方便性、准时性；市外出行增加对舒适性、安全性的需求.量化各种服务特性[13]，3个阶段出行广义费用fij,k、fjj′,α(j,j′)、fj′i′,k′计算如下：

(1)

fjj′,α(j,j′)=

(2)

(3)

式中：i=1，2, …，n1，i′=1，2，…，n2分别为城市A、B的交通小区编号；k=1，2，…，n3，k′=1，2，…，n4，分别为城市A、B内的交通方式；α(j,j′)=1，2，…，n5，为城市A、B间的交通方式；j=1，2，…，n6，j′=1，2，…，n7，分别为城市A、B的对外结点编号，对外结点包括城市车站及对外出入口.θχ为属性系数，χ=1，2，…，7；eij,k、rij,k、cij,k、pk、hij,k、sk分别为由小区i以交通方式k到达对外结点j的经济性、快速性、方便性、准时性、舒适性和安全性.

出行链中旅客广义费为

fii′,kα(j,j′)k′=fij,k+fjj′,α(j,j′)+fj′i′,k′

(4)

计算fij,k的关键是确定运输距离dij,k，即

(1)市内dij,k的计算，假设旅客选择最短路出行.k代表步行、自行车、出租车、小汽车时，dij,k取lij,a；k代表公交时，取lij,b；k代表城市轨道时，因其站点覆盖率低，需将接驳距离转化为轨道运输距离，接驳方式考虑步行、自行车、公交车，则

dij,k=Ψij,rlij,c

(5)

(6)

式中：lij,a(lij,b、lij,c)分别为距离小区形心i与车站j最近的道路结点(公交站点、轨道站点)间的最短路距离，利用Transcad加载区域路网求出.Ψij,r为修正系数，dij,r为接驳距离，分别由距离小区i(车站j)最近的道路结点、轨道站点间的最短路距离两部分构成.vr为城市轨道运行速度；pa、pb、pc分别为不同接驳距离内步行、自行车、公交车的分担率.参考文献[14]，接驳距离在500～3 000 m内，分担率为57.04%、16.05%和26.91%；大于3 000 m，分担率为0、14.81%和85.19%.当全程选择小汽车时，计算距离小区i形心最近的道路结点至对外出入口j的最短路距离.

(2)城际间djj′,α(j,j′)的确定，不同交通方式在对外结点j和j′之间的运行线路固定，因此运输距离取定值.

1.3 客流分担率模型

旅客一般选择使自身出行广义费用最小的交通组合方式，本文采用改进的多项Logit模型[15]求解在出行链中不同交通组合方式的分担率.

由城市A小区i至城市B小区i′的旅客各阶段分别选择交通方式k、α(j,j′)、k′的概率pii′,kα(j,j′)k′为

(7)

(8)

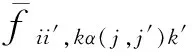
采用最大似然法标定参数，有

f(θ/p)=p(N1,N2,…,Nm/θ)=

(9)

(10)

式中：N为旅客数；m为交通组合方式.

2 双层目标选址模型

2.1 模型假设

考虑因站点选址不同造成的前期建设成本差异，后期运营的能源消耗、设备维护、折旧费用与线路走向有关，本文不予考虑.旅客总量及其出行空间分布已知.

2.2 模型结构

2.2.1上层模型

上层模型以最低的建设成本，吸引更多旅客选择城际铁路出行，使经济效益最大化.

(11)

qii′,kα(j,j′)k′=qii′pii′,kα(j,j′)k′

(12)

式中：I为城际运营者经济效益；a(j,j′)=r、φa(j,j′)分别为城际铁路及对应票价；qii′为OD对ii′的旅客量；pii′,kα(j,j′)k′、qii′,kα(j,j′)k′分别为选择城际铁路的概率及旅客量；xτ为站点τ建设成本；yτ为决策变量，设置站点τ，yτ取1，否则取0.

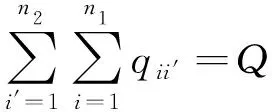
(13)

(14)

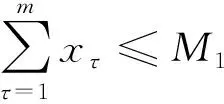
(15)

(16)

式中：Q为旅客总量，M1、M2分别为允许的最大投资费用、站点布设数量.

2.2.2下层模型

在考虑城际铁路运营者经济效益的同时，应结合旅客出行分布，优化城际站点布局，合理引导旅客出行选择，使旅客出行广义费用之和最小.

(17)

式中：J为出行链中旅客出行广义费用之和.

3 模型求解

双层目标模型实质为非线性非凸的离散选址问题，采用一种启发式方法，改进离散粒子群算法，求解模型的Pareto最优解.Pareto最优的相关定义如下：

设XA和XB是双层目标模型的两个可行解，称XA占优XB，记作XA≻XB.若

I(XA)≥I(XB)

(18)

J(XA)≤J(XB)

(19)

则解XA称为Pareto最优解.若

∃X:X≻XA

(20)

则称PS为Pareto最优解集.记为

PS={XA|∃X:X≻XA}

(21)

离散粒子群算法中粒子通过跟踪个体及全局最优位置迭代找到Pareto最优解，其搜索空间的速度及位置由式(22)～式(24)确定.

vδφ(t+1)=wvδφ(t)+c1r1(pBestδ-xδφ(t))+c2r2(gBest-xδφ(t))

(22)

S(v)=1/(1+exp(-v))

(23)

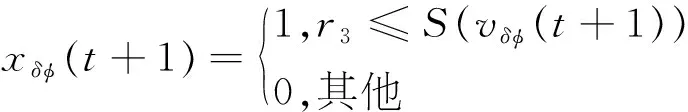
(24)

式中：t为迭代次数；w为惯性权重；c1、c2为加速系数；r1、r2、r3为区间[0，1]的随机数；vδφ、xδφ分别为粒子δ速度向量、位置向量第φ个分量；pBestδ为粒子δ的个体最优解；gBest为群体的全局最优解；s(v)为Sigmoid函数.

针对离散选址的具体特点，参考文献[16-18]对算法做如下改进：根据解的空间分布特征设计基于小生境的最优解选择法，保证外部档案中解的均匀分布；引入变异算子，在粒子附近区域搜索新的非劣解，避免过早的局部收敛.

改进离散粒子群算法流程如图2所示.

算法中各步骤处理如下：

(1)维护外部档案

个体与全局外部档案维护均按照可能出现的各种情形[16]进行更新.

(2)选择全局最优解

根据外部档案中每个解的适应度值，采用与适应度值成比例的轮盘赌概率方法选择.

(3)选择个体最优解

为使个体粒子快速跟踪全局最优解的变化，从个体外部档案中选择与全局最优解距离最近的成员作为个体最优解.

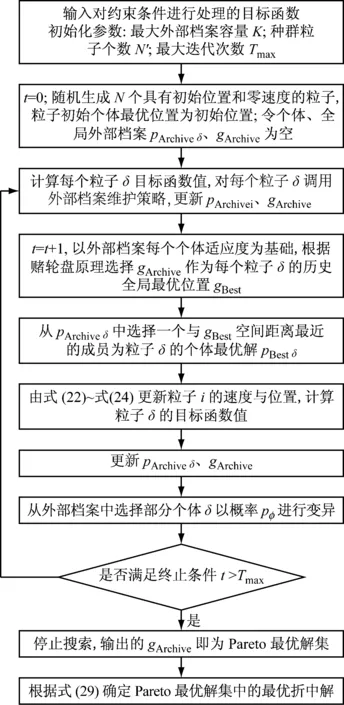
图2 改进算法流程

(4)适应度的计算

根据小生境共享机制[19]，定义外部档案中粒子xδ的适应度，即

(25)

(26)

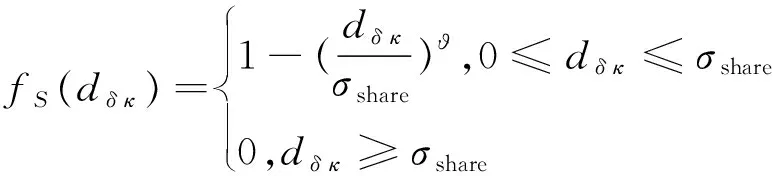
(27)

式中：NS为小生境内粒子数量；sδ为粒子δ的共享度；fS(dδ)为粒子xδ、xκ间的共享函数；ϑ为形状参数，一般取1 或 2；σshare为共享距离；变异概率pψ=0.3；dδ为粒子间距离，采用海明距离如下：

⊕xκ g)

(28)

(5)最优折中解

采用线性加权形式，根据不同需求μ1和μ2取不同值，得相应的最优折中解，即

maxZ=μ1I-μ2J

(29)

μ1+μ2=1

(30)

(6)约束条件的处理

不满足式(20)或式(21)时，将该粒子目标值设为较小值，在寻优过程中无法占优.

4 实例分析

将广珠城际铁路线(区域城际铁路主轴系统)在珠海市内的站点布设方案为研究对象，其中线路在广州市内的站点布设方案已确定.在2016年可行性研究调查基础上，进行数据校核及参数标定，验证模型的合理性及算法的可行性，并分析相关参数敏感性.

4.1 模型计算

本线主要服务于珠海市金湾区和斗门区，与已运营的广州南至珠海城际共同分担广珠客运通道的交通压力.因此以珠海市金湾区、斗门区及广州市区作为研究范围，将珠海市金湾区和斗门区共划分为66个交通小区，将广州市274个交通小区合并为70个中区，如图3所示.在可行性研究研调查基础上得到线路运营远期珠海至广州的旅客出行OD矩阵.

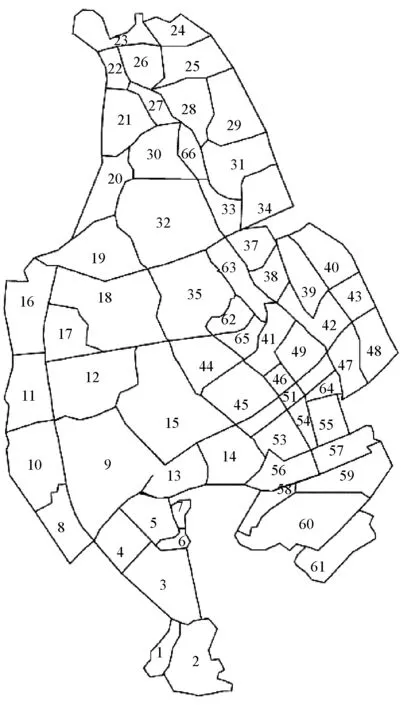
广珠城际线工可研阶段珠海段内总概算中，11个备选站点的建设费用如表1所示.

远期各运输方式广义费用参数采用2016年调查数据，其中珠海城市轨道交通、广珠城际线广义费用参数分别采用广州地铁、广州南至珠海城际线运营数据，分别如表2、表3所示.

将可研阶段居民出行意愿调查有效问卷数N=6 872，运输组合方式m=73代入式(15)，得θ1=0.081 3、θ2=0.066 9、θ3=0.045 6、θ4=0.106 2、θ5=0.122 8、θ6=0.110 8、θ7=0.166 4.

最大投资建设费用M1=1.095×108元；站点最大布设个数M2=4，粒子编码分量与站点编号相对应，共享距离δshare=11.经试算，其他参数设置如下：

初始种群数N′=20，最大迭代次数Tmax=200，个体、全局外部档案容量分别为4和8，加速系数c1=c2=1.55，惯性权重w=1.2.

站点布设需重点考虑城际铁路作为公共交通的公益性，在旅客较少的区域仍需增设站点，政府通过划分沿线土地使用权给运营者作为经济补偿，因此权重系数取μ1=0.4，μ2=0.6.

将上述数据代入模型，利用改进离散粒子群算法求解得到城际站点布局的Pareto最优解及最优折中解，结果分别如图4和表4所示.

由图4可知，当迭代至37代时，Pareto最优解集中的粒子趋于稳定，算法收敛.

表1 备选站点建设费用

注:α取值20为投资回收年限;上标(1)、(2)、(3)表示同一行政区域内的不同备选站点

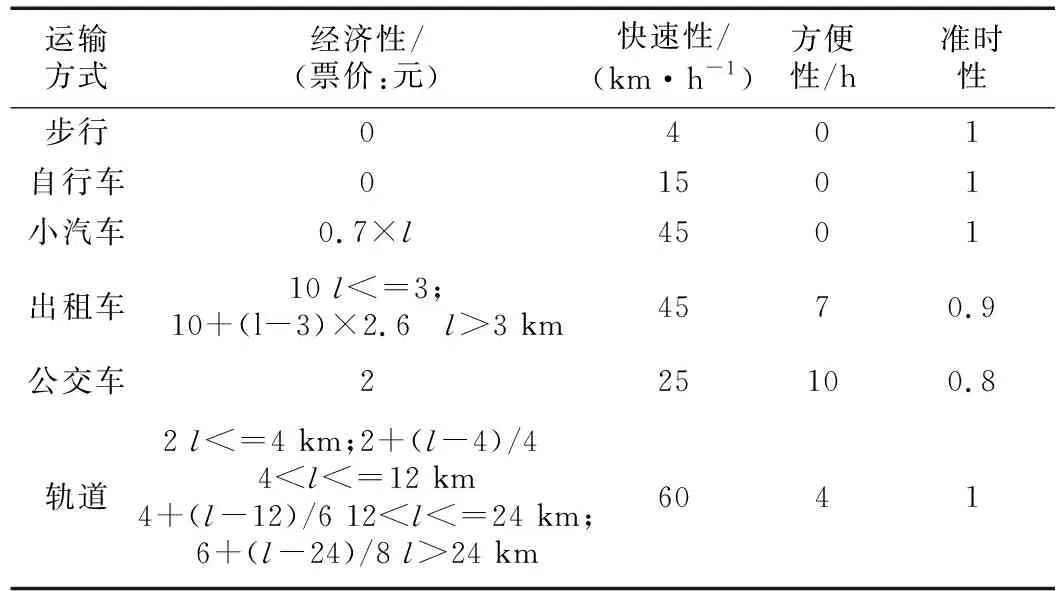
表2 市内运输方式广义费用参数

表3 城际间运输方式广义费用参数

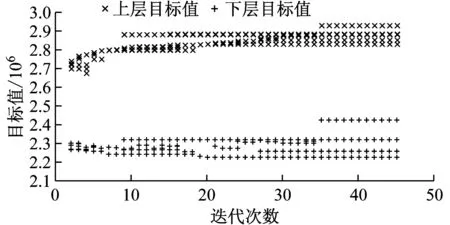
图4 迭代次数与Pareto最优解

结果表明，模型的Pareto最优解体现了提高城际铁路运营收入与降低旅客在出行链中广义费用总和的矛盾关系，以此为基础实现两者的均衡，为城际铁路站点选址提供更全面的决策依据.在μ1=0.4和μ2=0.6时，选址方案的粒子编码为{10010001001}，即布设4个站点，分别位于珠海机场、斗门(1)、金湾(2)、莲州(2)，与本线工程可研阶段珠海市内的站点布设方案相同，验证了权重系数取值的假设，即站点布设方案体现城际铁路的公益性，通过增加车站数量提高可达性，方便旅客出行.

表4 Pareto最优解及选址方案

此外，城际铁路分担率随站点数量的增加而提高，但增幅较小.在不考虑站点建设成本的前提下，布设方案为{10000000000}的票价收入仍大于布设方案分别为{10010000000}、{10010010000}这两种情况，说明虽然站点布设个数的减少会带来一定的客流损失，但仍会吸引大量的属于其他拟布设城际站点的客流，并通过不同起始站点票价的差异弥补客流损失带来的经济效益影响.这一方面与旅客总量及其空间分布位置有关，另一方面也说明相比于其他城际运输方式，城际铁路由于其快速、安全、舒适等特点，即使在站点可达性相对较低的条件下对客流仍具有较大吸引力.

4.2 敏感性分析

利用Matlab分别计算当旅客时间价值(vot)、站点日均建设成本、城际铁路票价以2%为单位在-20%～+20%区间变化时对选址方案的影响，见表5.

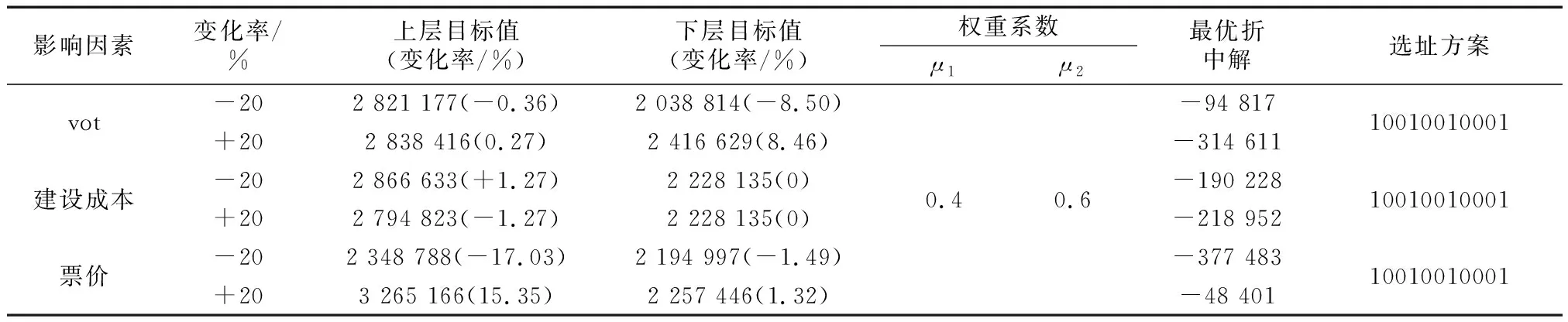
表5 不同因素变化对选址方案的影响

当vot、站点日均建设成本、城际铁路票价变化率在[-20% +20%]时，站点选址方案保持不变.相比于不同选址方案间的上层目标值，下层目标值的差异对选址方案的影响更显著.vot对下层目标值的影响更大，将进一步扩大下层目标值对选址方案的影响；建设成本和票价对上层目标值影响更大，但不能完全弥补下层目标值之间的差异，与其他方案相比，推荐选址方案的下层目标值对于决定最优折中解的优势十分明显，因此选址方案不变.

5 结论

既往城际站点选址研究中往往忽略或简化市内出行，为此，本文提出以出行链为基础的城际铁路站点选址双层目标模型，充分考虑市内交通对旅客城际间出行交通方式选择的影响，运用改进离散粒子群算法求解模型，更加切合实际地分析城际铁路站点选址对其运营收入及旅客出行费用的影响.

经实例验证，城际站点选址中提高城际铁路运营收入与降低旅客在出行链中的出行广义费用总和是相互矛盾的，以模型Pareto最优解为基础实现两者的均衡，可为站点选址提供更全面的决策依据；城际铁路站点布设个数的减少未必导致城际铁路车票收入降低，受到不同站点票价差异及旅客空间分布的影响；当vot、站点日均建设成本、城际铁路票价在-20%～+20%之间变化时，不会对站点选址方案产生影响.

本文上层目标仅考虑站点建设成本与运营收入，未来研究可进一步加入站点选址与后期运营成本(包括电力消耗、材料折旧、设备维护等)等因素的影响.此外，模型构建还需考虑城际站点布局的前瞻性，即如何将站点布局对城市发展的影响作为评价指标纳入站点布局优化模型.