波音平整度评价方法的局限性分析
2018-09-11凌建明刘诗福
凌建明, 刘诗福, 李 萌, 袁 捷
(1.同济大学 道路与交通工程教育部重点实验室,上海 201804;2.上海机场(集团)有限公司虹桥国际机场公司,上海 200335)
机场道面的检测是保证机场建设发展及安全运行的基础,不平整的机场道面不仅会加速飞机构件的疲劳损伤,影响驾驶员对飞机的操控以及对仪器的读数,也将造成乘客的不舒适、加速机场道面的损坏.在我国2009版《民用机场道面评价管理技术规范》中[1],规定“道面平整度评价一般采用国际平整度指数(IRI)作为指标;不具备测试条件时,可采用3 m直尺法进行评价,其中IRI以算术平均值分段评价,3 m直尺以最大间隙的平均值进行评价”. 3 m直尺法操作简单,使用方便,但是测试效率低,且机场跑道停航时间短使得该方法应用场景有限.国际平整度指数IRI是基于1/4车模型的反应类平整度指标,于1986年由世界银行在巴西进行道路平整度试验时提出[2].尽管IRI来源于路面平整度,但目前中国、巴西、意大利、墨西哥及南非等国家都直接采用IRI评价跑道或者滑行道的评价指标,意大利等国家也间接采用了IRI[3].然而,凌建明等通过对比分析在相同不平整激励下飞机和汽车在构造、质量、减振系统等方面上的差异,结果表明飞机和汽车的动力学响应相差较大,机场道面和公路路面的平整度应加以区分[4];国际民航组织(ICAO)[5]和美国联邦航空管理局(FAA)[6]等认为1/4车难以反映飞机本身的动力学响应;凌建明[7]通过建立飞机的动力学模型及Chen等[8]利用APRas商业软件,都表明IRI的敏感波长与飞机滑跑的敏感波长相差较大;Loprencipe研究表明IRI评价机场跑道可能会得到不正确的维修措施[9];刘诗福[10]和周晓青[11]等都基于随机生成的不平整激励反算得到修正后的IRI评价标准.可见,目前国内外已经逐渐意识到基于IRI指标评价机场道面平整度的局限性.因此,我国在2018年修订的《民用机场道面评价管理技术规范》中引入了第3个评价指标波音平整度指数(Boeing Bump Index,BBI).
波音平整度方法是为数不多的针对跑道平整度的评价方法之一[12],美国机场道面管理系统PMS中也推荐使用BBI指标[13];Loprencipe等对比分析了BBI指标与其他指标,结果表明BBI更适用于评价道面平整度[9];Emery等研究表明IRI指标和BBI指标没有可比性,且BBI的平均值太小,评级结果太保守[14].但是,波音平整度方法是基于B727飞机滑行的疲劳损伤试验、针对跑道上单个隆起建立的,在实际使用时仍会有一些局限性.因此,本文在介绍波音平整度评价方法的基础上,开发计算BBI的程序;并基于ADAMS/Aircraft,建立典型机型的虚拟样机模型,通过实测的跑道不平整激励和正弦函数不平整激励,分析了几点关于波音平整度方法评价跑道平整度的局限性,研究结果可为波音平整度方法的应用边界提供方法支持.
1 波音平整度指数
1.1 Boing Bump方法
为了解决功率谱密度方法无法区分小振幅多波动还是大振幅少波动的问题,波音公司于20世纪60年代开始机场道面平整度相关研究工作.基于波音飞机滑行的疲劳损伤实验,即满载的B727飞机,在接近起飞速度130~200节(241~371 km·h-1)之间的主起落架疲劳试验,提出了基于最大隆起高度(Bump Height)和隆起长度(Bump Length)两者关系的评价指标,相应的评价标准如图1所示[12].
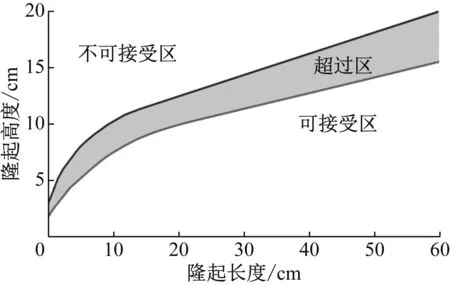
图1 波音公司机场道面平整度评价标准[12]
本质上,Boeing Bump是“可变”的直尺长度-最大间隙控制的方法,因此BBI也是断面类的指标.评价标准主要分为3个区:
(1)可接受区:可接受区的下限为隆起高度恒为0的水平直线,而上限为图中阴影部分的下边界曲线;满足乘客舒适度要求及不干扰飞机驾驶员对仪器读数的平整度不应超过可接受区的上限值.
(2)超过区:道面隆起位于超出区范围,道面的不平整对飞行员与乘客造成明显的不适感,严重影响仪器读数和操作,并对起落架产生过载影响,位于超过区的跑道需要即时维修.
(3)不可接受区:满足飞机起落架疲劳寿命的平整度不应落于不可接受区范围,对于不可接受区的跑道需要马上关闭.
1.2 BBI计算
采用图1中的Boeing Bump评价跑道平整度是费时繁琐的,因为对纵断面每一点都需尝试不同的“直尺”长度.因此,在Boeing Bump评价方法的基础上,美国FAA提出了波音平整度指数[13].纵断面某点上的BBI值通过以下步骤计算[4]:
(1)对于选定的一个点,计算不同直尺长度下的隆起高度与隆起长度;
(2)对每一“直尺”长度,分别计算其隆起长度可接受的隆起高度(可接受区域的上限值);
(3)对每一“直尺”长度,计算测量的隆起高度与可接受的隆起高度限值的比值;
(4)对所有的纵断面高程点重复(1)~(4).
计算点的BBI值取第(3)步中计算得到的最大值.当BBI小于1.0,则平整度位于可接受区域;当计算结果大于1.0且小于1.25,则平整度位于超过区;当计算结果大于1.25,平整度位于不可接受区.
1.3 BBI程序
研究利用VBA语言,根据上述BBI的计算算法,开发计算BBI的程序TJ-BBI如图2所示.TJ-BBI有4个模块,“使用方法”模块介绍了该软件的使用步骤;“数据读取”模块是加载间距为0.25 m的实际高程文件;“提交计算”模块可对原数据按照BBI的算法,得到每点的BBI值;“计算结果”模块通过各类图表展示原始高程函数,波音平整度指数以及其分布.经过比较,TJ-BBI与美国FAA开发的ProFAA软件在BBI的计算方面结果一致.
2 典型机型虚拟样机模型
机场跑道平整度的评价与飞机滑跑的动力学响应密切相关.《2014 中国内地飞机运营情况报告》中,波音和空客公司的机型占中国内地运营客机的93.36%,而B737-800与A320-200机型占了近56%,考虑到两种机型在尺寸以及起落架构型上相当,本文以A320-200作为研究对象,建立相应的虚拟样机滑跑模型,分析BBI指标和评价标准在预测飞机动力学响应方面存在的问题.
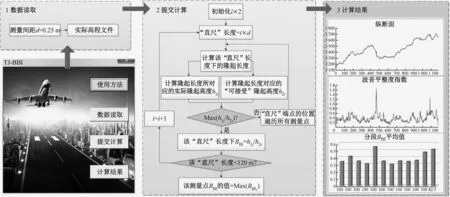
图2 BBI求解流程
2.1 建模流程
首先利用三维建模软件CATIA建立飞机机身、起落架等的三维几何模型,然后将集合构件导入到ADAMS/Aircraft中,定义运动质量属性、运动副(约束)、力等,以及建立相应的通信器;然后建立子系统,进一步组装成全机模型.用于滑跑仿真分析的虚拟样机全机模型包括机身子系统、前起落架子系统、前机轮子系统、主起落架子系统、主机轮子系统,如图3所示.
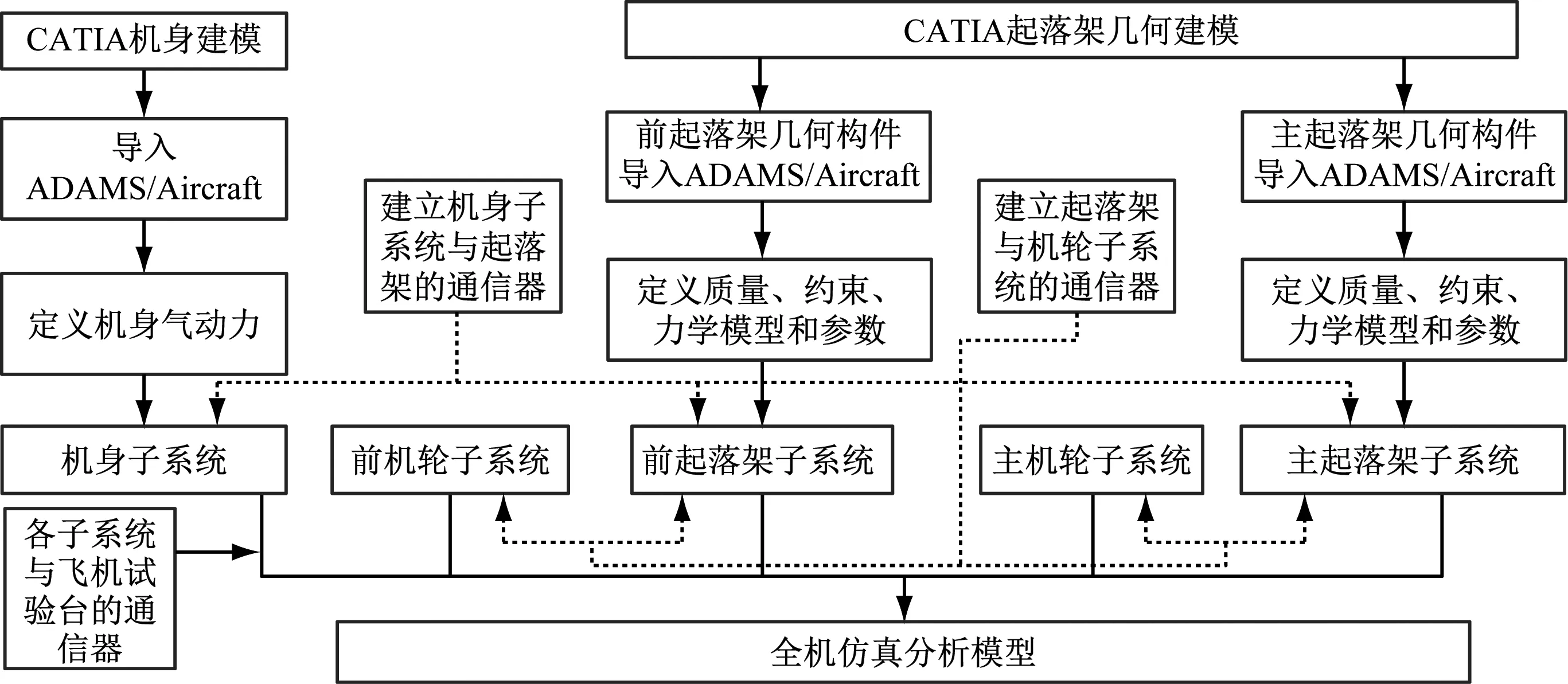
图3 虚拟样机建模流程
2.2 滑跑仿真
在ADAMS/Aircraft模块中,各子系统与仿真试验台(testing)之间通过建立通信器(communicator)装配成全机模型.将定义好的不平整道面模型与全机模型结合,设置好滑行速度后,软件可以自动生成动力学微分方程组,并调用求解器求解,可得到飞机各部位的动力学响应指标,进而实现虚拟样机在道面上的仿真分析,如图4所示.
3 跑道不平整激励
由图4可知,虚拟样机模型的滑跑动力学响应除了与样机本身相关之外,还与跑道道面的不平整激励形式密切相关,研究主要采用实测纵断面高程以及正弦函数纵断面高程两种不平整激励形式,分析BBI指标的局限性.
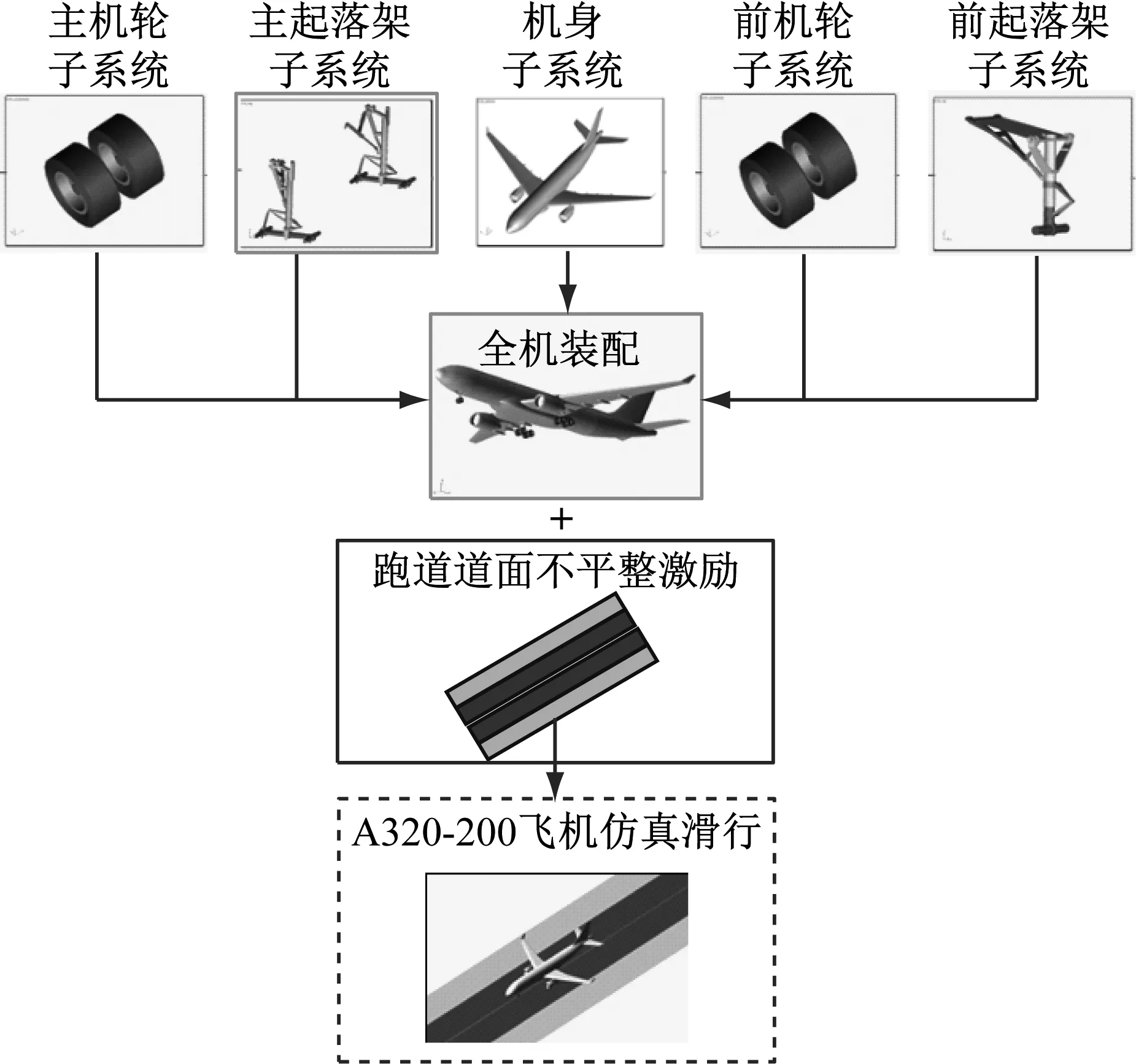
图4 A320-200飞机的滑跑仿真
3.1 实测纵断面高程
美国联邦航空总局FAA、波音和空客公司曾实测了世界范围内37条跑道的纵断面高程数据[15]:通过车载加速度传感器测得信号,然后积分计算得到道面的断面高程,并通过高通滤波消除传感器的漂移误差.本文将该37条跑道数据分别去噪后作为跑道不平整激励,其中某条跑道的实测数据如图5所示.
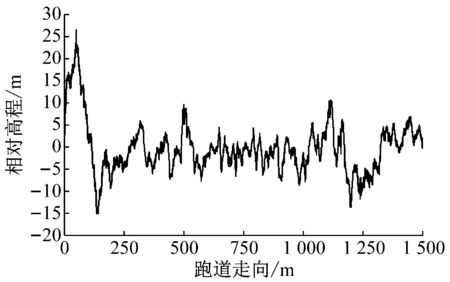
图5 某条跑道的纵断面高程实测数据
3.2 正弦函数纵断面高程
机场道面随着服役时间的增加,在纵断面上会产生微波隆起,这种起伏可以近似地用余弦函数来表示[16],本文也通过这种假定的不平整形式研究BBI的局限性.
(1)
式中:H为振幅;λ为波长;y为纵断面的相对高程,x为沿跑道的纵向距离.
4 结果分析
4.1 多个连续隆起的问题
对于一些服役时间较长且地基处理不当的机场跑道,在纵断面上可能会存在多个连续的隆起.现假定两种情况:① 500 m长的跑道道面上只存在一个振幅为0.2 m、波长为40 m的隆起,其他区域平整,如图6a所示;② 500 m长的道面上刚好存在两个连续的振幅为0.2 m、波长为40 m的隆起,其他区域平整,如图6b所示.
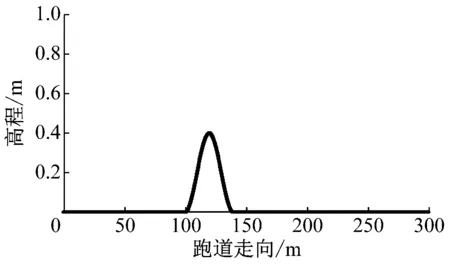
a 单个隆起
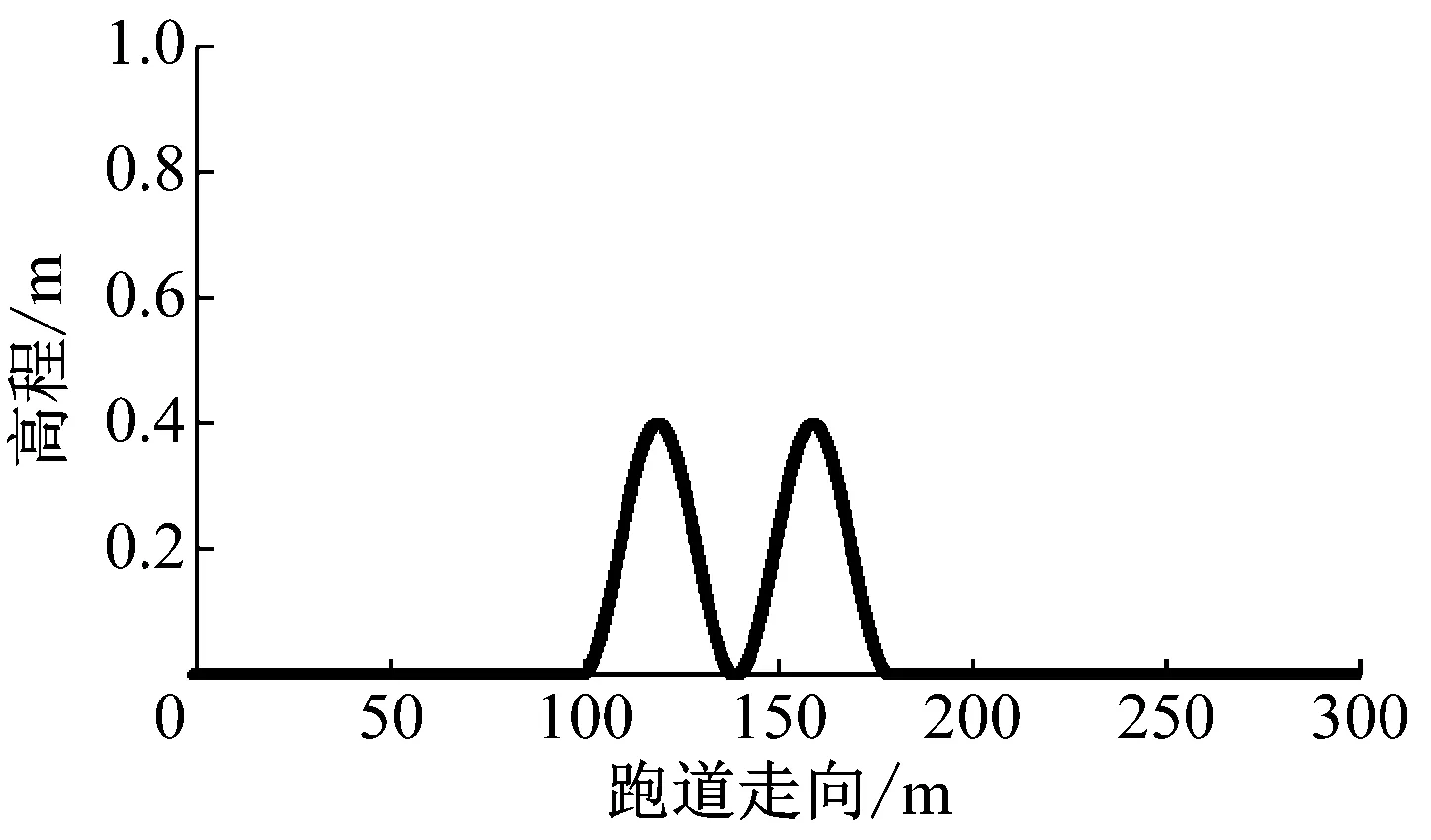
b 两个隆起
当A320-200飞机以200 km·h-1的速度在跑道上滑跑,其重心处的竖向加速度响应分别如图7a和7b所示.
可见,经过单个隆起时,飞机振动响应在1.8~3.6 s之间,其重心处的竖向加速度值经历了两次大振幅的起伏;而经过两个隆起时飞机振动响应在1.8~4.5 s之间,其重心处的竖向加速度值只经历了3次大振幅的起伏,这是因为前一个隆起的第2次大振幅还没有消散,就与后一个隆起的第1次大振幅叠加;这也表现在飞机经过单个隆起时,其响应的振幅最大值为8.6 m·s-2,而经历连续两个隆起时,其响应的振幅值达到了10.1 m·s-2,相比增加了17.4%,这表明两个连续的隆起对飞机的动力学响应起到了叠加作用.
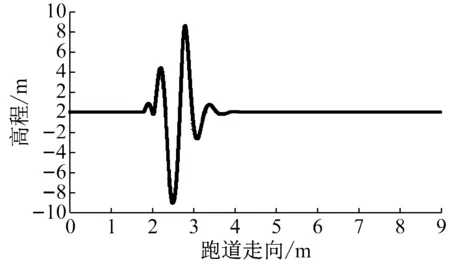
a 单个隆起的振动响应
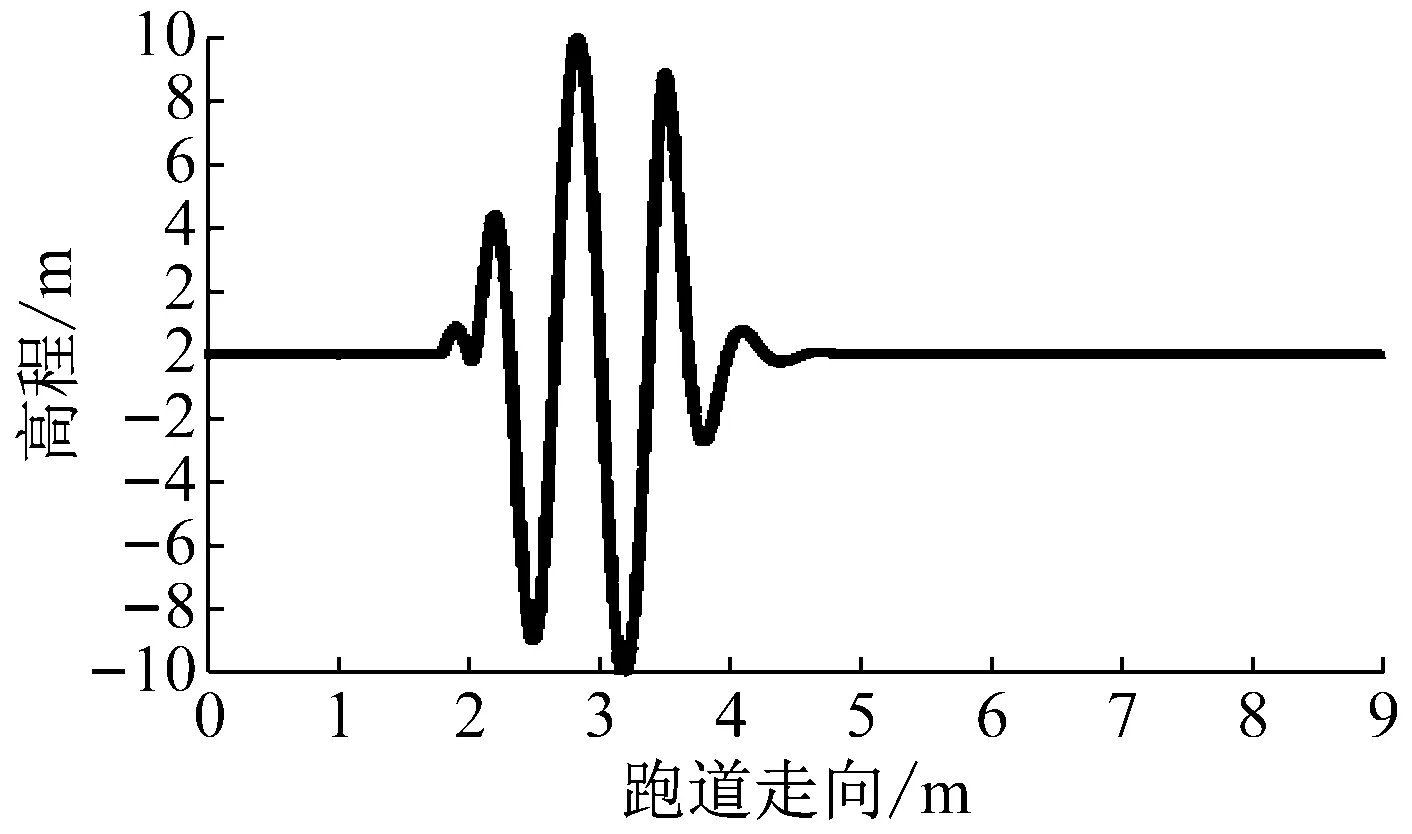
b 两个隆起的振动响应
单个隆起和两个隆起的不平整跑道的BBI分布如图8所示.单个隆起的不平整跑道的BBI值从50 m处开始增加,并且在125 m处达到最大值,并在200 m后逐渐趋于0;多个隆起的不平整跑道的BBI值从50 m处开始增加,并且在100~200 m之间值较大,并在250 m后逐渐趋于0.但是,两个连续隆起的BBI最大值都是0.19,这也表明,第1个隆起和第2个隆起对BBI值不存在叠加效应,不能有效表征飞机在多个连续隆起中滑行时实际的振动响应特征.事实上,不能有效处理多个隆起的叠加效应,是断面类平整度评价指标相对于反应类的缺点之一,BBI指标应辅以反应类的平整度评价指标进行综合评价.
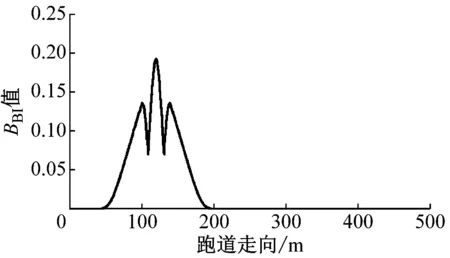
a 单个隆起
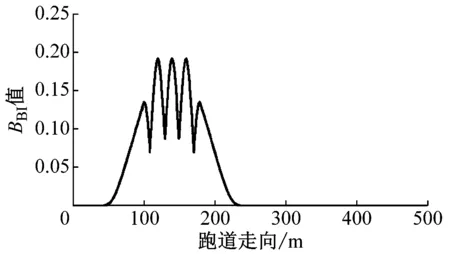
b 两个隆起
4.2 最不利速度的问题
飞机在滑跑过程中会受到气动力的作用,其中升力的大小随着速度增大而增大.图9为A320-200飞机起落架轮胎荷载系数随速度的变化情况,包含了6个速度下的统计结果,可看出在0~80 km·h-1时动载系数先增大,在80~200 km·h-1时动载系数逐渐减小,在150 km·h-1时飞机对道面的冲击与静载相同,而在200 km·h-1时只有静载的0.93倍.这是因为在速度较低时机翼提供的升力较小,道面对轮胎的冲击荷载随滑跑速度增大而不断增加,而当速度增大到一定程度,机翼可以提供较大的升力,导致冲击荷载减小,动载系数较小.由第1节介绍的波音平整度方法可知,其评价标准是基于满载飞机的起飞速度,但事实上由于升力的存在,起飞速度并不是最不利速度,因此图1中的评价标准过于宽松,在实际应用时可修正到更严格.

图9 起落架轮胎荷载系数随速度的变化
4.3 评价指标单一的问题
机场道面的平整度应该综合考虑驾驶员操纵飞机的安全性、乘客的不舒适性以及飞机起落架的疲劳寿命等.本文通过收集A320-200飞机滑跑时重心处的加速度均方根值、驾驶舱加速度均方根值以及主起落架动载系数,得到三者的拟合关系如图10和图11所示.
主起落动载系数[17]、重心处的加速度均方根值[18]、驾驶舱加速度均方根值[19]的评价标准如表1所示.当主起落架动载达到1.3时,根据图10和图11拟合公式计算得到重心处以及驾驶舱的加速度均方根值分别为0.24和0.63 m·s-2.对比表1中的评价标准可知,驾驶舱加速度均方根已经落在了超过区,这表明相比于主起落架的动载系数,驾驶舱的加速度均方值更应该值得关注.从这个角度分析,只考虑主起落架疲劳寿命的BBI评价标准也过于宽松,在实际应用时应根据驾驶员的反应而修正到更严格.
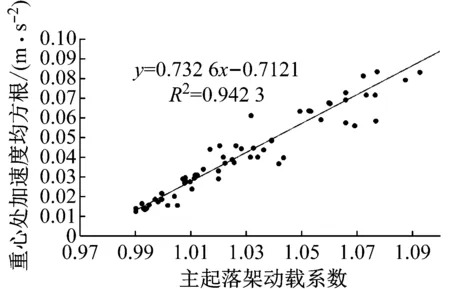
图10 重心处加速度与主起落架动载系数关系
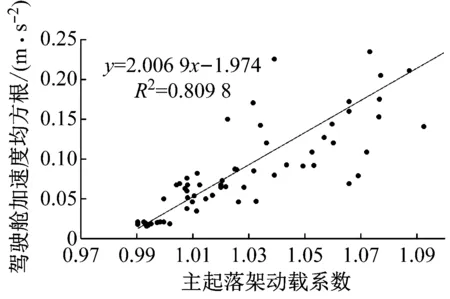
图11 驾驶舱加速度与主起落架动载系数关系
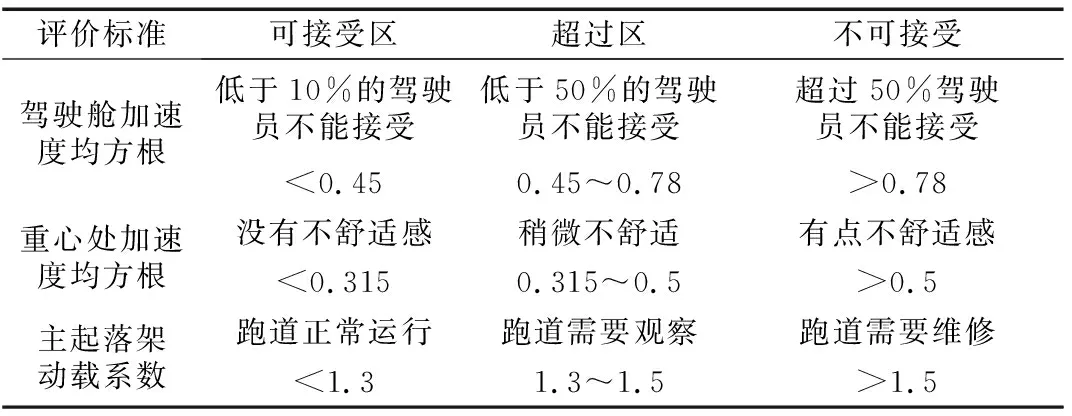
表1 基于不同指标的评价标准
4.4 评价机型单一的问题
波音平整度方法基于的是B727飞机的滑跑实验,目前该类机型已退出民航市场.表2中对比了B727-200和目前市场上常用机型A320-200以及B737-800在起飞重量以及前后起落架之间的距离.无论是在重量上还是在前后起落架之间的距离上,B727-200都要比其他两种机型大.
本文只分析起飞重量上对飞机响应的影响.在虚拟样机模型中保证其他参数不变,只改变机身子系统的重量参数,飞机在跑道上滑跑时,其重心加速度均方值对重量的敏感性如图12所示.在其他条件相同的情况下,飞机质量越大,振动响应越小,B737-800和A320-200飞机重量比B727-200飞机重量的重心加速度响应高13%和17%.从该角度分析,基于B727飞机的波音平整度方法评价标准也是偏于宽松的,在实际应用时应基于民航市场上常用机型而修正到更严格些.

表2 不同机型的参数对比
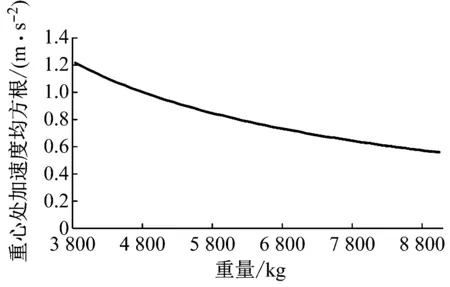
图12 重心加速度随飞机重量的变化
5 结论
(1)介绍了波音平整度评价方法,开发了计算BBI的程序,并通过虚拟样机技术,建立目前民航市场典型的A320-200机型,在实测跑道不平整和正弦函数不平整激励下,进行了飞机的滑跑实验,从指标本身以及评价标准指出了波音平整度方法应用于评价机场跑道平整度的4点问题.
(2)作为断面类的平整度评价指标,BBI不能有效处理跑道上连续隆起对飞机动力响应的叠加效应,该指标应用时还应辅以其他反应类指标进行综合评价.
(3)波音平整度方法的评价标准是基于B727飞机在接近起飞速度下的主起落架疲劳寿命,但是由于升力的存在,飞机最不利速度并非是起飞速度;相比于主起落的疲劳寿命,不平整跑道对驾驶舱振动更应该受到关注;目前民航市场上主要机型的质量都比B727要小,振动更为剧烈,因此波音平整度方法的评价标准过于宽松.
(4)波音平整度方法引用到我国机场跑道的平整度评价时,建议和IRI反应类指标综合应用,且BBI的标准需重新考虑最不利速度、多个评价指标以及多个常用机型的耦合修正,科学地反映飞机的动力学响应,合理评价机场跑道的平整度.
