大跨连续钢箱梁设计

蒋定衍

（上海市政设计研究总院集团佛山斯美设计院有限公司，广东 佛山528200）

0 引言

随着我国钢材产业逐渐由产能短缺进入产能过剩，钢结构加工工艺显著提高，钢结构更环保和可持续发展、全寿命周期经济竞争性强、人力资源更节省等优势逐渐凸显，钢结构桥梁在公路桥梁建设中表现出强劲的的竞争性。同时，为贯彻落实《交通运输部关于推进公路钢结构桥梁建设的指导意见》，各地也都在积极探索，大力推广公路钢结构桥梁的建设。

1 主梁构造

某工程的主梁采用（50+86+50）m变截面钢箱梁，梁高按2次抛物线变化，截面形式为单箱三室。中支点处梁高3.6 m（高跨比1/23.89），边支点和跨中位置梁高2.12 m（高跨比1/40.56），箱梁顶宽16.5 m，主梁横断面如图1所示。

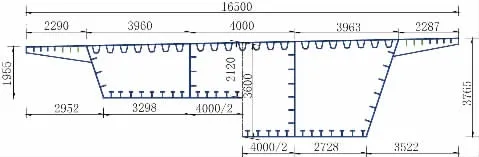
图1 主梁横断面图

2 主要计算参数

（1）一期恒载：钢材容重 γ=78.5 kN/m3，按照施工图实际自重考虑。

（2）二期恒载：

铺装：沥青混凝土 100 mm ，γ=24 kN/m3；

防撞护栏：15 kN/m/侧。

（3）车辆作用：公路-I级。

（4）支座沉降：不均匀沉降L/3 000。

（5）温度：体系升温：+30℃；体系降温：-30℃。

（6）温度梯度：正温差+14℃；负温差-7℃。

3 荷载组合

桥梁重要性系数：1.1。

（1）标准组合一：恒+活+支座沉降。

（2）标准组合二：恒+活+支座沉降+系统升温（+30℃）+正温差（+14℃）。

（3）标准组合三：恒+活+支座沉降+系统降温（-30℃）+负温差（-7℃）。

（4）基本组合一：1.2恒+1.4活+支座沉降。

（5）基本组合二：1.2恒+1.4活+支座沉降+1.05系统升（降）温+1.05温度梯度正（负）温差。

4 平面静力计算

以Midas Civil建立了结构的平面杆系模型，对结构在自重、二期恒载、活载、支座不均匀沉降，以及温度力等荷载工况下进行平面静力分析，按照最不利组合进行验算（见图2）。

图2 钢箱梁计算模型

4.1 承载能力极限状态分析

结构按公路桥规JTG D60-2015第4.1.5条承载能力极限状态效应组合进行承载力验算，主梁的承载力和内力包络见图3、图4所示。

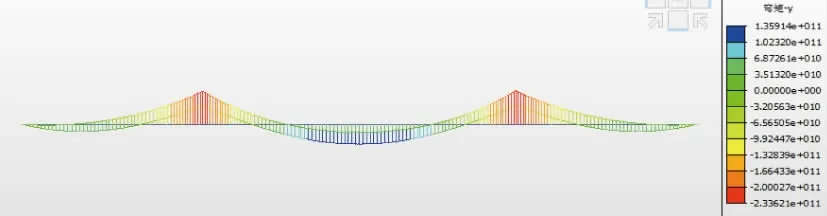
图3 正截面抗弯承载能力包络图

图4 正截面抗剪承载能力包络图

4.2 正常使用极限状态分析

按《公路钢结构桥梁设计规范》（JTG D64-2015），连续钢箱梁有效分布宽度可按下式计算：

中间支点断面：

式中：b为主梁腹板间距的一半或悬臂板的宽度；l为换算跨径。

计算结果如表1所列。

表1 截面有效分布宽度系数表

考虑剪力滞后箱梁上下翼缘应力如表2~表4所列。

5 结构活载挠度计算

根据《公路钢结构桥梁设计规范》（JTG D64—2015）中4.2.3条，计算竖向挠度时，应按结构力学的方法并应采用不接冲击力的汽车车道荷载频遇值，频遇系数为1.0，由此计算的结构扰度如图7、图8所示，86 m跨中上挠33 mm+下挠88 mm=121 mm。

表2 标准组合二上下翼缘应力一览表 MPa

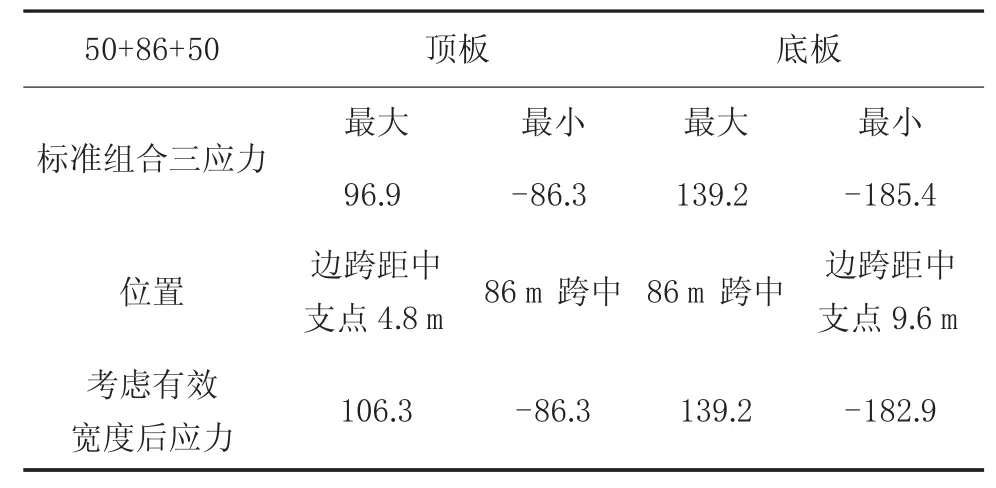
表3 标准组合三上下翼缘应力 MPa

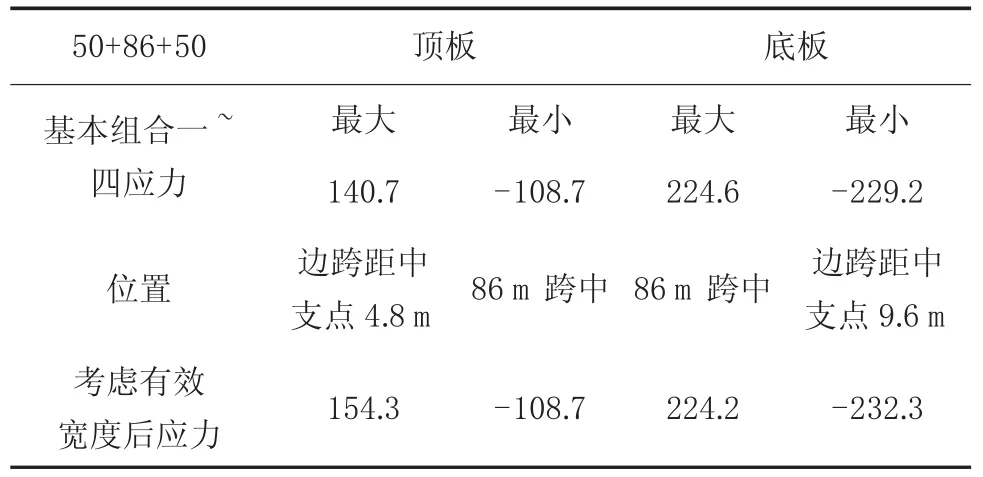
表4 基本组合一～四上下翼缘应力一览表 MPa

图7 活载MAX挠度包络图

图8 活载MIN挠度包络图

6 结构抗疲劳验算

根据《公路钢结构桥梁设计规范》（JTG D64—2015）中5.5.2条，采用疲劳荷载计算模型Ⅰ，取用等效的车道荷载，集中荷载0.7Pk，均布荷载0.3qk，四车道布载。计算结果见表5所列。

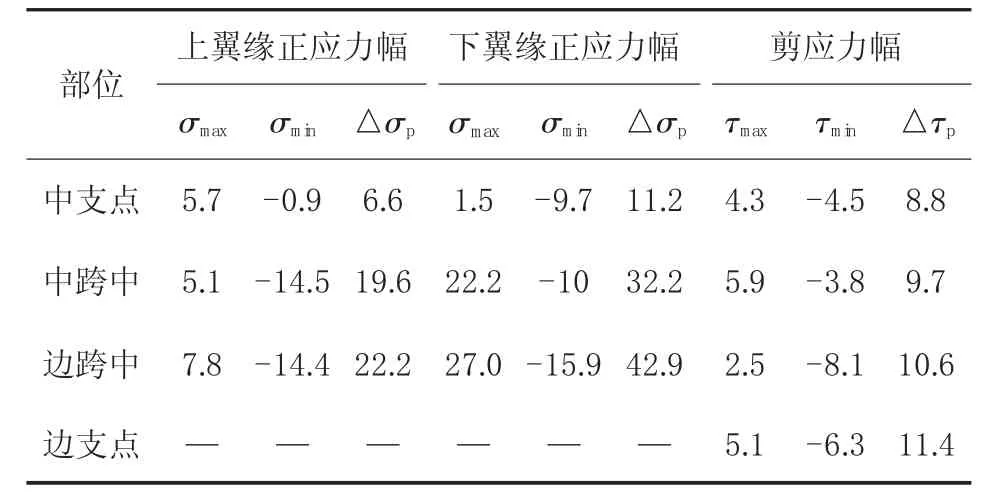
表5 结构各部位应力幅一览表 MPa

采用疲劳荷载计算模型得到的各部位应力幅满足下列公式：

（1）上翼缘母材正应力幅：

（2）下翼缘母材正应力幅：

（3）母材剪应力幅：

7 结语

通过以上计算分析，可得出如下结论：

（1）结构在最不利组合中，最大拉应力224.2 MPa，最大压应力-232.3 MPa，应力满足规范要求。

（2）梁端腹板剪切应力106.1MPa，小于155MPa,剪应力满足规范要求。

（3）活载作用下，结构中跨86 m跨中最大的挠度为 121 mm＜86 000/500=172（mm），刚度满足规范要求。

（4）结构抗疲劳验算满足规范要求。