一种具有组合正则的图像恢复方法

刘晓光

(西南民族大学计算机科学与技术学院，四川 成都 610041)

近年来，正则化方法在数字图像处理、支撑向量机等应用领域得到了深刻的关注[1-3].作为重要应用之一，若令∈RP、g∈Rq分别代表原始图像与受污染图像，数字图像恢复技术通过求解如下能量函数的最小值点f∗恢复图像f＾：

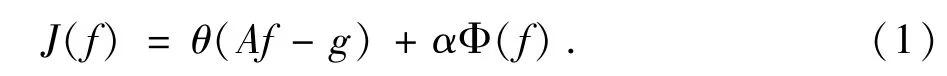
其中，A∈Rq×p代表由设备的老化与振动、恶劣的成像环境等原因引起的污染系统.函数θ：Rq→R为向量Af、g误差大小的度量，函数Φ(f)(正则项)代表图像f的部分先验信息，α＞0(正则参数)用来调节函数θ与Φ的平衡.

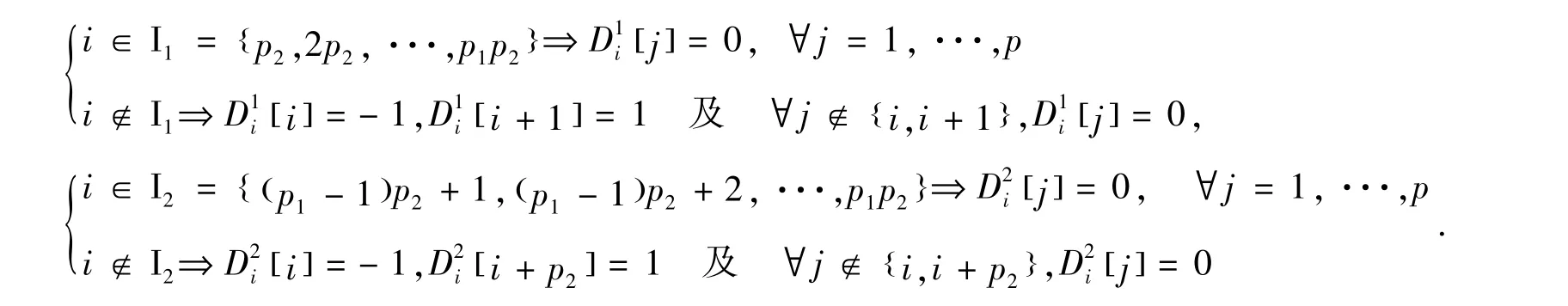
能量函数结构表明，势能函数φ在正则化数字图像恢复技术中起着关键作用，为此人们展开了深入的研究[1-4].其中，理论和数值实验结果表明吉洪诺夫类正则，如Φ(f) ＝像像素值平滑转换区域有出色的恢复性能，且其可微性使得相关算法具有较高的计算效率，从而被广泛应用[4-7].但该类正则使恢复图像过度平滑，不适用于恢复图像边缘等纹理信息[7-9].

对于吉洪诺夫类正则的上述不足，非凸非光滑势能函数：

λt/(1+ λt) ， log(λt+1) ， tλ(λ ∈ (0，1)) ，等表现出了好的恢复性能[8-17].特别地，Nikolova M等人于文献[9]中对非凸非光滑势能函数能够保护图像边缘等纹理信息的性能给出了理论证明，为该类势能函数的后续研究与应用奠定了坚实的基础.然而，文献[2，12-19]中指出一阶非凸非光滑势能函数在保护图像边缘等信息的同时会引起台阶效应，即在图像像素值平滑转换区域中形成若干虚假边缘类信息，降低图像恢复质量.为此，二阶差分近年来被广泛用在非光滑势能函数中保护图像纹理信息，图像恢复质量得到了一定提高.但非凸非光滑性决定了相应二阶非凸非光滑势能函数对台阶效应的克制存在局限性[9].

本文研究了一种以组合一阶非凸非光滑势能函数和吉洪诺夫势能函数为基础的图像恢复方法.如上所述，一阶非凸非光滑势能函数用来保护图像边缘等纹理信息.吉洪诺夫势能函数在保证恢复方法对图像像素值平滑转换区域有出色恢复性能的同时，克服前者所引起的台阶效应.类似文献[9，11]等，针对势能函数非凸非光滑性带来的数值计算困难，渐进非凸方法(GNC)及交替方向法被用来求解相关问题.最后，数值实验结果表明了推出方法的的恢复性能.

1 具有非凸非光滑组合势能函数的图像恢复方法

近似最小值点.其中，将函数Jεk(f)的近似最小值点设置为问题：mfinJεk+1(f) 的起始点 (k ＝ 0，1，2…，n-1)，从而通过依次获得具有较高性能的初始值提高能量函数(2)的图像恢复性能.对任一确定εk(k＝0，1，2…，n)，采用如下交替方向法求解.

当函数φ非凸非光滑时，组合吉洪诺夫和一阶非凸非光滑势能函数，能量函数(1)转化为：

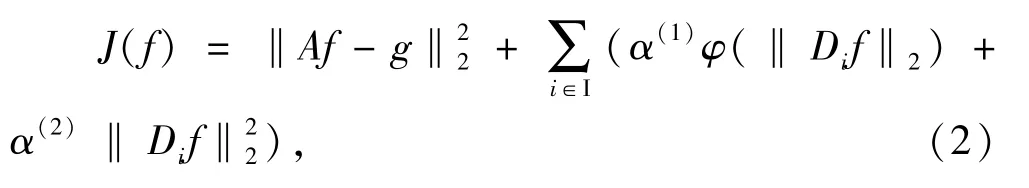
其中α(1)＞0、α(2)＞0均为正则参数.为克服非凸非光滑性引起的数值计算困难，类似文献[9]，文中采用GNC方法求解上述能量函数的近似最小值点.该方法利用一组非光滑近似势能函数φεk逼近函数φ(0 ＝ ε0＜ ε1＜ … ＜ εn＝1，φεn＝ φ)，并逐次求解如下函数序列的：

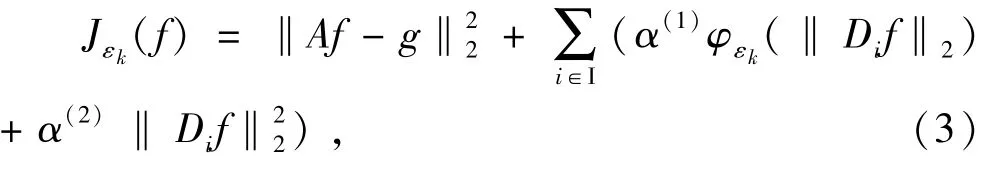
图1 原始图像Fig.1 Original images

2 数值实验

为说明算法1的恢复性能，下面给出数值实验对比结果.其中对比算法选为文献[7]中吉洪诺夫类正则恢复方法和文献[9]中一阶非凸非光滑图像恢复方法，程序参看http：//www.math.hkbu.edu.hk.测试图像为具有平滑区域和较多边缘信息的Cameraman(256×256)，Jetplane(512×512)两个传统测试图像(图 1).实验在 MATLAB2016a，Core(TM)为1.80GHz，RAM为4GB的测试环境下完成.

实验中，CPU运行时间度量算法效率，峰值信噪比(PSNR)、信噪比(SNR)：

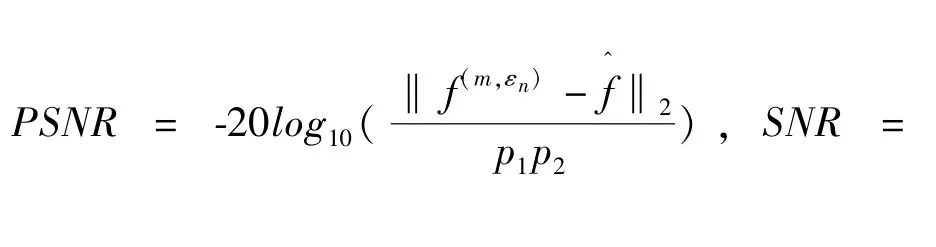
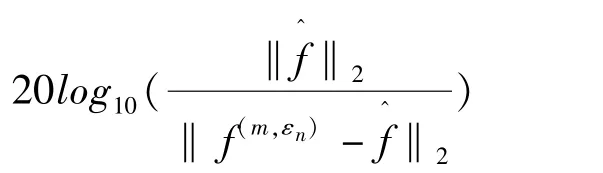
衡量图像恢复质量.如文献[9]中所示，ω1的初值设定为1.1，且以1.8倍的速度递增，τ＝1，n＝10，令α(1)＝0.015，α(2)＝0.03，非凸非光滑势能函数φ及相应近似势能函数φεk选取如下：

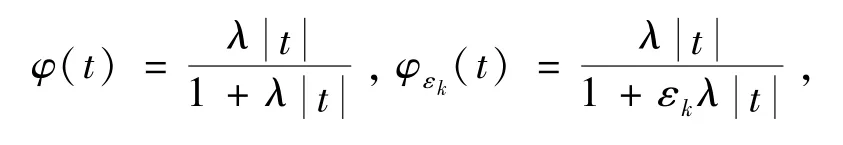
其中λ＝1.模拟污染源为支撑集分别为5×5(σ ＝1)、7×7(σ ＝1.5)、9×9(σ ＝2)的如下二维高斯函数：

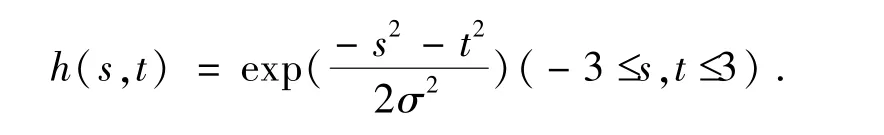
加性噪声设定为均值为0，标准差分别为0.05，0.1，0.15的高斯噪声.

首先，以两种不同的恢复情形为例，在图2-3中形象的说明算法1及对比算法的图像恢复效果.(1)针对Cameraman图像，高斯噪声标准差与污染函数支撑集分别选取为0.05、5×5，图2(a)代表受污染的Cameraman图像，图2(b-d)分别代表文献[7]中方法、文献[9]中方法、算法1的恢复结果.(2)针对Jetplane图像，高斯噪声标准差与污染函数支撑集分别选取为0.15、9×9，图3(a)代表受污染的Jetplane图像，图3(b-d)分别代表文献[7]中方法、文献[9]中方法、算法1的恢复结果.

图2 污染函数支撑集为5×5，高斯噪声标准差为0.05时Cameraman图像恢复效果图(a)污染图像 (b)文献[7]中方法恢复图 (c)文献[9]中方法恢复图 (d)算法1恢复图Fig.2 The restored Cameraman images，where the standard deviation of Gaussian noise is 0.05，the support is 5 × 5.(a)Blurred image (b)Image restored by the algorithm in[7](c)Image restored by the algorithm in[9] (d)Image restored by the algorithm 1

图3 污染函数支撑集为9×9，高斯噪声标准差为0.15时Jetplane图像恢复效果图(a)污染图像 (b)文献[7]中方法恢复图 (c)文献[9]中方法恢复图 (d)算法1恢复图Fig.3 The restored Jetplane images，where the standard deviation of Gaussian noise is 0.15，the support is 9 × 9.(a)Blurred image (b)Image restored by the algorithm in[7](c)Image restored by the algorithm in[9] (d)Image restored by the algorithm 1

观测上述两种情形可知，算法1在有效恢复图像平滑区域的同时，更好地保护了边缘等纹理信息，恢复图像有更好的视觉效果(相关恢复数据参看表1和表2).针对不同的实验环境，表1和表2中给出了相应的的数值实验结果，数据表明算法1所恢复图像的SNR、PSNR值均优于两种比较算法.其中，当测试图像为Cameraman图像时，针对文献[7]、[9]中方法恢复结果，算法1所恢复图像的SNR值至少分别提高0.04db、0.02db，PSNR 值至少分别提高 0.06db、0.04db.当测试图像为 Jetplane图像时，针对文献[7]、[9]中方法恢复结果，算法1所恢复图像的SNR值至少分别提高0.05db、0.03db，PSNR值至少分别提高0.02db、0.03db.同时，可以看到由于测试图像具有较多边缘等纹理信息，文献[9]中算法所恢复图像SNR、PSNR值在多数情形下高于文献[7]中方法恢复结果.

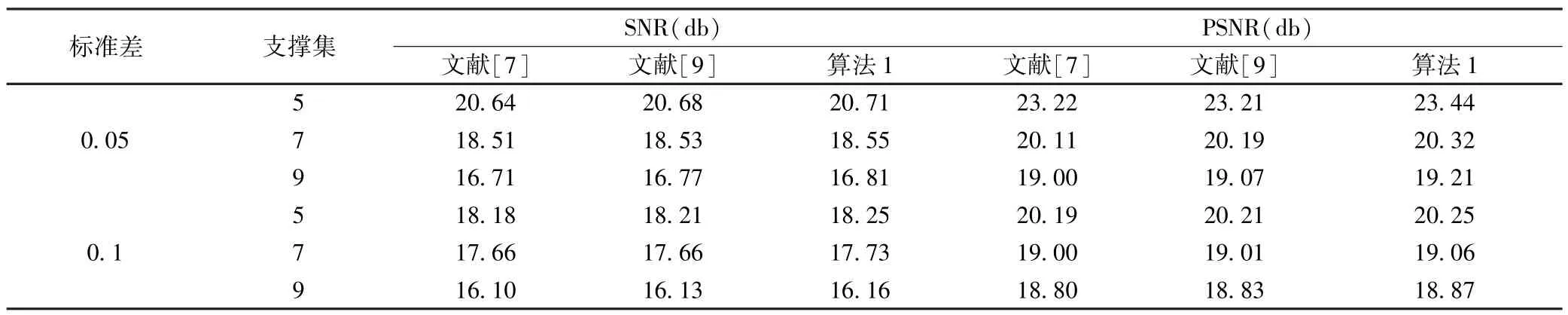
表1 Cameraman图像恢复结果Table 1 The restored results ofCameraman image

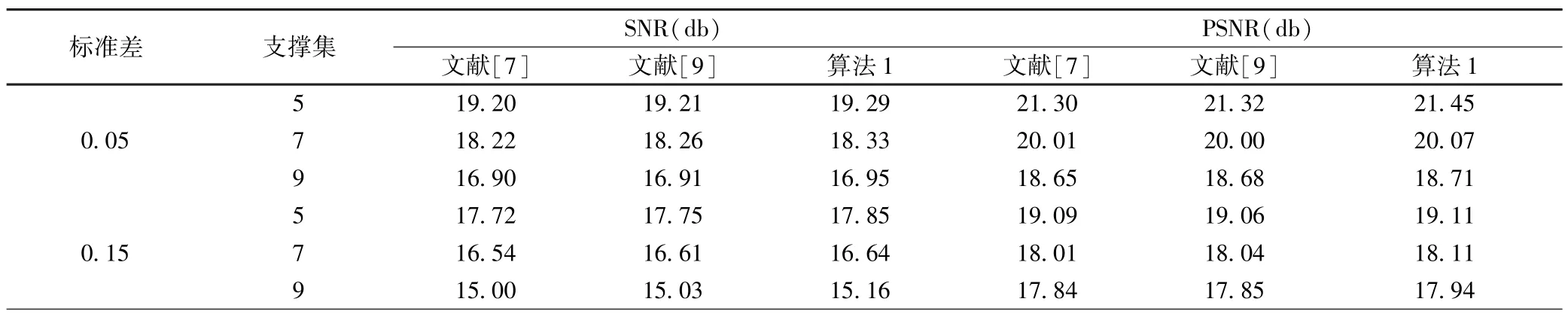
表2 Jetplane图像恢复结果Table 2 The restored results ofJetplane image

最后，需要指出的是实验数据表明相同环境下算法1运行效率较文献[9]中方法有所提高，但在少数情形下略低于文献[7]中吉洪诺夫类正则方法(参看表3).

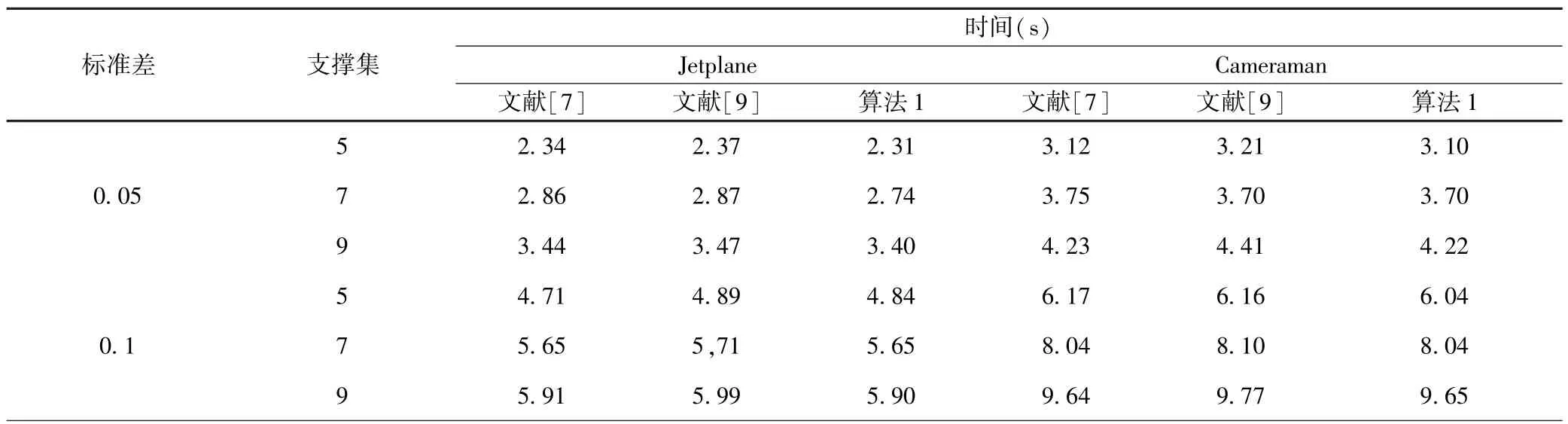
表3 运行时间对比结果Table 3 The comparison results of running time

3 结论

吉洪诺夫势能函数对图像像素值平滑转换区域具有很好的恢复性能，但不能够很好地保护图像边缘等纹理信息.相反，理论与数值实验结果表明一阶非凸非光滑势能函数对图像纹理信息有较好的的保护能力，但会引起台阶效应.为了能够同时利用上述两类势能函数的优点，克服相应不足，本文推出了一种以组合吉洪诺夫与一阶非凸非光滑势能函数为基础的图像恢复方法.实验结果表明，针对包含像素值平滑转换区域和较多边界等纹理信息的图像，本文所推出的算法具有更好的综合性能.