一类非线性电路方程的行波解

刘 倩，高 莉，姜 玥

(西南民族大学计算机科学与技术学院，四川 成都 610041)

1 引言

长久以来，非线性波动现象一直都是数学物理领域中备受关注的研究对象.而随着自然科学的蓬勃发展，涌现出了大量描述非线性波动现象的偏微分方程，比如KdV方程、Klein-Gordon方程、SchrÖdinger方程等等.如何理解这些方程解的物理意义并探索其长时间行为，行波解在其中扮演着重要的角色.近年来，人们已经发展出很多直接的方法寻找偏微分方程的行波解，比如Tanh函数法[1-2]、G’/G方法[3-5]、同伦摄动方法[6]、Adomian分解法[7-8]、变分迭代法[9-10]、ansatz方法[11-12]等.其中，G’/G方法因其简洁、高效的特点被广泛应用.

本文考察一类非线性电路方程[13]

它是著名的Boussinesq方程[14-15]

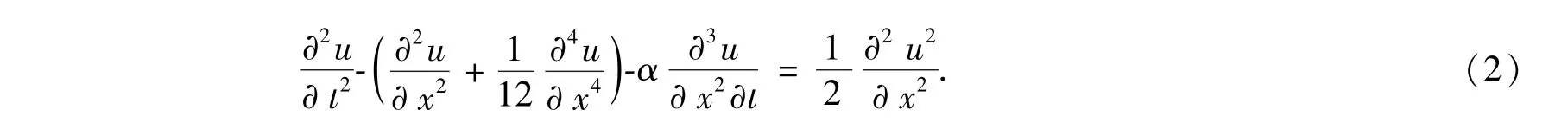
的变形和推广形式.作为一个带有耗散项的高阶不可积系统，方程(1)的行波解研究起来比较困难.我们利用齐次平衡法的思想和G’/G函数展开法，对其行波解的形式进行了假设，并将该偏微分方程约化为复杂的非线性代数方程组，借助计算机代数系统的符号运算功能求解该方程组，成功获得了电路方程包含sinh和cosh形式，sin和cos形式的行波解的精确表达式.这些解无论从理论的角度还是从应用的角度，对电路方程描述的非线性波动现象的理解和研究都有重要的意义.

2 电路方程的显式行波解

对方程(1)做行波变换u(x，t) ＝U(ξ)，ξ＝kx+ωt我们得到其行波系统如下：

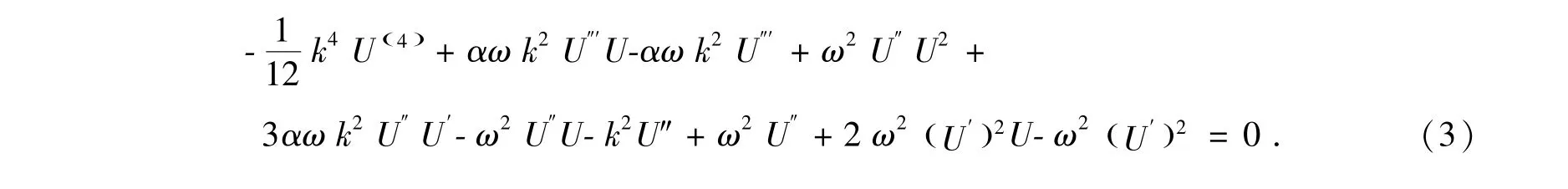
其中，a0，a1，a2为待定实参数，G(ξ)满足如下二阶方程

将U(i)(ξ)(i ＝1，..，4) 代入方程(3)，合并关于的同类项并令其系数为0，可得如下非线性代数方程组

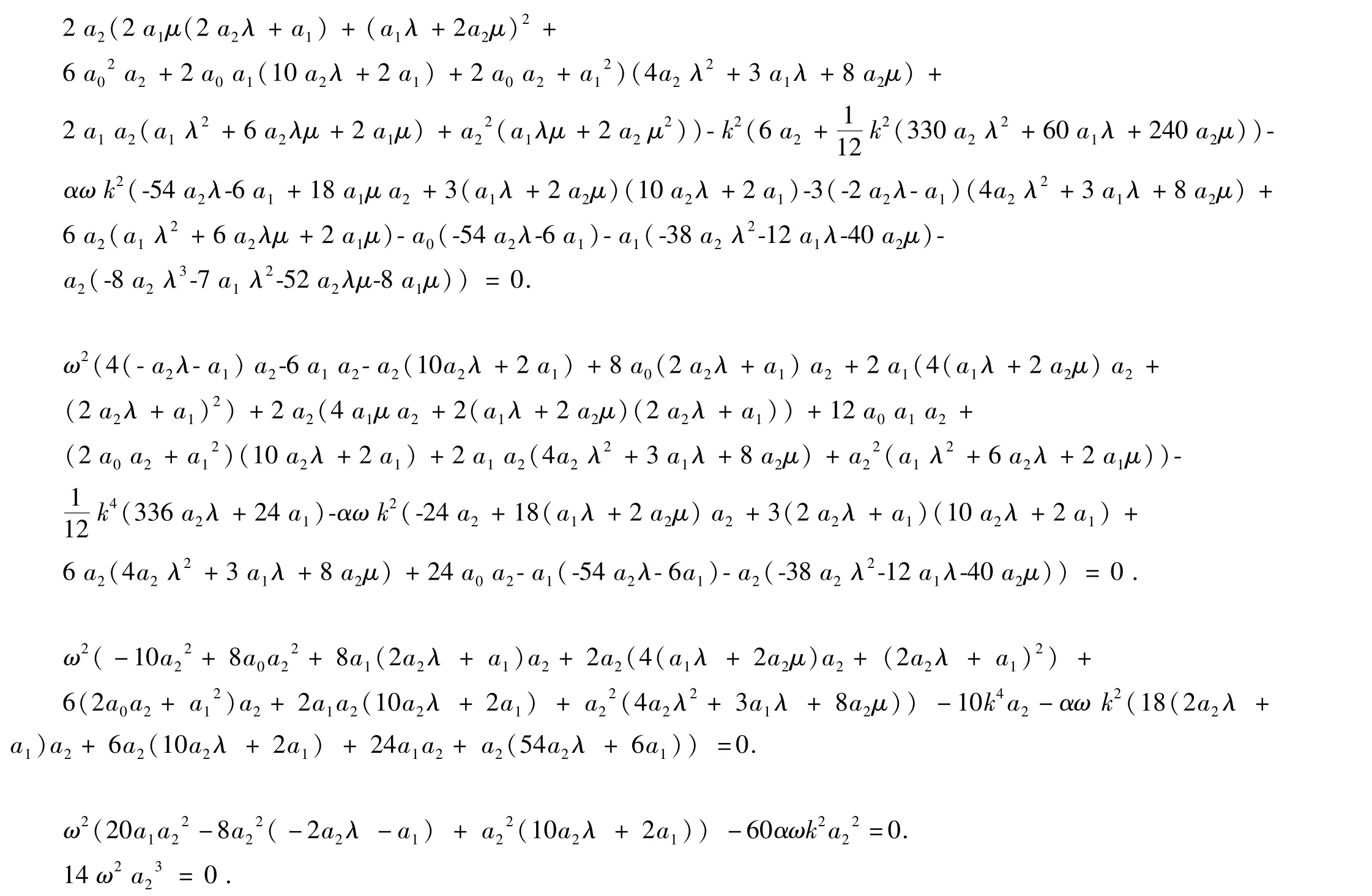
利用计算机代数系统求解上述方程组，可得

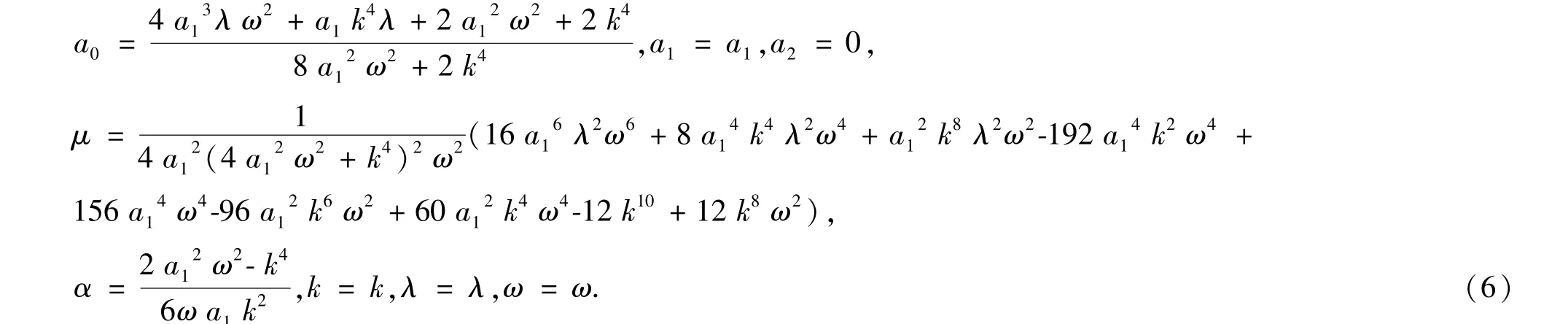
注意到二阶方程(5)有如下三种形式的解

当λ2-4μ ＞0时，

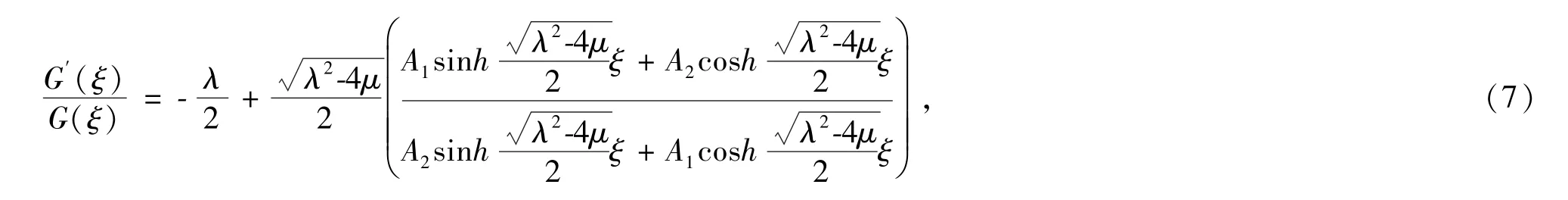
其中A1，A2为任意常数.

其中A1，A2为任意常数.

将(6)-(9)代入(4)，可获得电路方程(1)的三组行波解.

其中A1，A2为任意常数.

在三组解中，解组1和解组3为电路方程的孤波解，为直观了解其描述的波形，我们给出它们的数值模拟图(如图1所示).

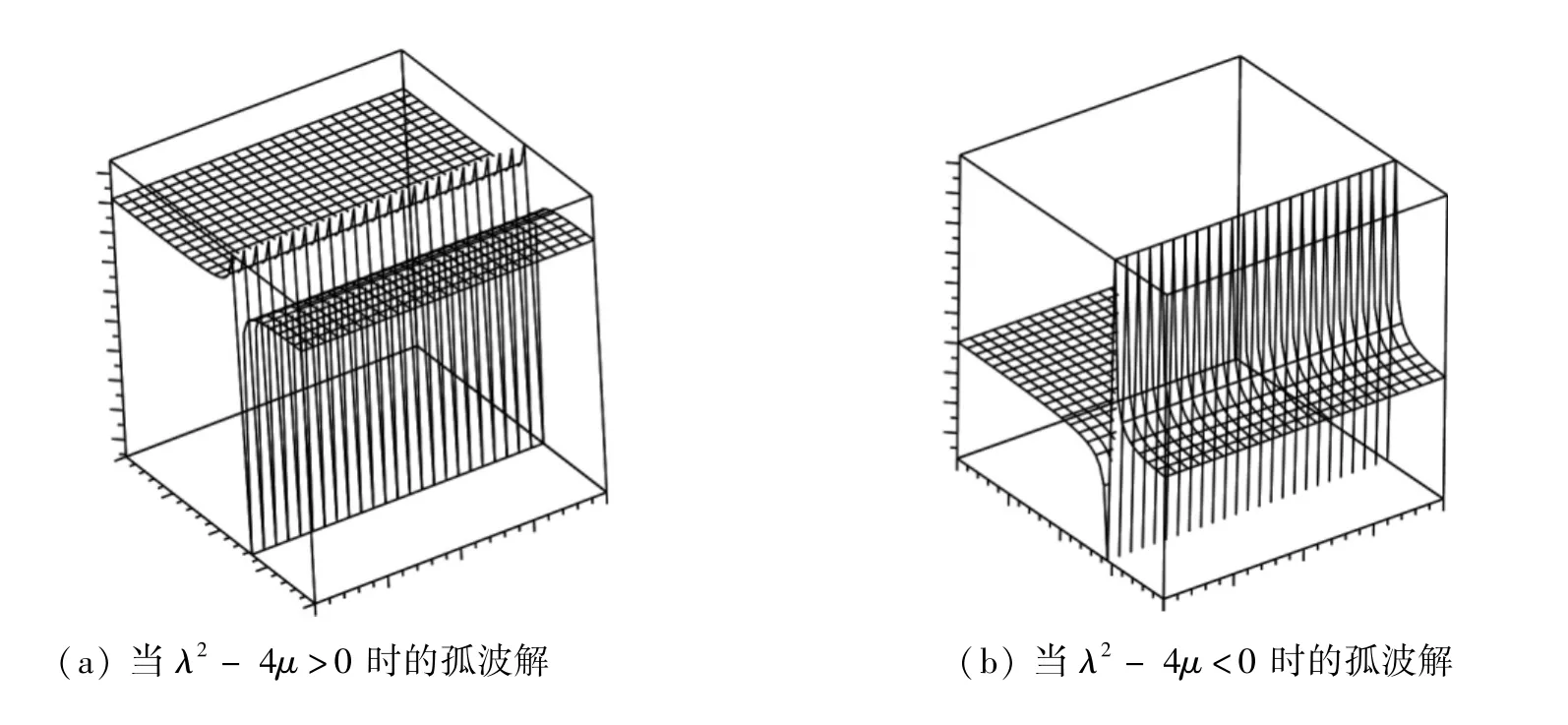
图1 电路方程的孤波解Fig.1 The solitary wave solutions of the circuit equation

3 结语

本文利用G′/G函数展开法求得了一类非线性电路方程多种类型的行波解，这些解尤其是孤波解对于理解方程描述的非线性波动现象的长时间行为有着重要作用，同时表明该方法对于求解高阶非线性偏微分方程非常有效.当然，该方程可能还有其他类型的行波解，比如无界行波解.但是由于方程具有高阶且非线性的特点，研究起来比较困难，所以目前关于其他类型的行波解的讨论结果很少，感兴趣的读者可以考虑用其他的方法来做进一步讨论.