创新驱动、教育发展与全要素生产率变化

王 婷，刘 毅，刘艳枫

(西南民族大学管理学院，四川 成都 610041)

1 引言及文献述评

中国经济增长由投入驱动向全要素生产率驱动的转型势在必行[1].在经济增速下降、发展方式转变和结构调整的新常态下，为经济增长保驾护航的投资、消费和出口的作用逐渐势弱，全要素生产率在推动经济增长中的重要作用愈加凸显.伴随资本边际报酬递减、“人口红利”逐渐消失和出口增速的回落，物质资本、劳动和出口在推动经济增长中显得后继乏力，为了助力中国经济跨越“中等收入陷阱”，为了实现中华民族的伟大复兴，转变发展方式、转换发展动力及增强发展动能已刻不容缓.

与传统发展动力不同，全要素生产率是指在要素投入水平既定的条件下，经济增长所达到的额外效率，它可弥补资本边际报酬递减的消极影响，具有长期可持续性，是经济增长经久不衰的引擎[1].因此，提高全要素生产率才是维持经济可持续发展的根本途径.

创新是提高全要素生产率的必由之路.然而如何提高全要素生产率，不同学者提出的路径并不完全一致.Zachariadis[2]通过对10个OECD国家的研究表明，提高R＆D强度可推动全要素生产率增长；郭庆旺和贾俊雪[3]的研究指出，技术进步和能力实现改善可提高全要素生产率；赵志耘和杨朝峰[4]认为全要素生产率提高的源泉在于技术进步和资源配置效应的改进.尽管对全要素生产率增长源泉的认识存在差异，但归根结底，全要素生产率的提高在于技术进步、制度创新、组织管理完善以及资源配置效率的改进等，而这些方面都离不开创新驱动的支持.因此，要乘势“大众创业、万众创新”，让创新在全社会蔚然成风，为全要素生产率的提高铺平道路，为经济的可持续发展鼓足后劲.

教育为创新提供有效的人力资本，是全要素生产率提高的智力源泉.创新是一个国家能够长久立足于世界民族之林的根本保障，如何维持创新的可持续性就成为全社会关注的焦点.创新是智力活动的产物，需要借助人力资本的载体，而教育发展直接关系到人力资本培养水平的高低，高水平的人力资本将激发更多的创新动力和活力.因此，教育与创新息息相关，创新的顺利推动离不开教育的持续发展.同时，教育也为全要素生产率的持续提升提供了源源不断的智力支撑.尽管受教育年限是全要素生产率的重要影响因素[5]，但不同的受教育水平对全要素生产率的影响存在差异[6]，不过人力资本依然是全要素生产率的促进因素[7]，且高质量的人力资本对应更高水平的全要素生产率[8].然而，人力资本的错配将降低这种促进作用，而人力资本配置效率的改进，需要进一步扩大教育规模[9].正所谓“百年大计，教育为本”，为了“两个一百年”目标的顺利实现，提高全要素生产率是根本途径，加强创新是必然选择，提升教育水平和质量是长久之路.

世界经济在低迷中蹒跚前行，中国经济步入“三期叠加”，下行压力依然较大.尽管国内经济长期向好的基本面没有变，但提质增效、转型升级的要求更加迫切，如何提高经济增长质量和效益，如何增强经济发展的可持续性，众多学者提出的路径较为一致：提高全要素生产率水平.如何提高全要素生产率，加强创新是首选，“十三五规划”已把创新发展放置于新发展理念的首位，同时，发展教育也必不可少，科教兴国战略和人才强国战略也在稳步推进.

然而，现阶段我国经济增长对要素投入的依赖依然较大[10]，且由于2008年的金融危机，全要素生产率步入了下滑通道[11]，其对经济增长的贡献度随之下降，经济的可持续发展面临挑战，那么，随之而来且亟须解决的问题在于，创新驱动和教育发展是否依然为全要素生产率的推动因素?对此加以研究的文献尚不多见.基于此，本文在前人研究的基础上，借助计量经济模型和最新相关数据，进一步论证和阐述创新驱动、教育发展和全要素生产率的动态演化关系，以此挖掘新常态下经济可持续发展的可行路径.

2 模型建立与数据来源

2.1 模型建立

在对创新驱动、教育发展与全要素生产率变化的关系进行分析时，所面临的首要问题为如何对全要素生产率进行估算.对此，目前主要存在四种方法：增长核算法、生产函数法、随机前沿分析法以及数据包络分析法(Malmquist指数法)[12-13].增长核算法简单直观，但不适于具体实证分析[14]；随机前沿分析法把全要素生产率视为一个独立的状态空间变量，以此从残差中分离出来，因而全要素生产率的估计更为精确，但本文的实证数据无法满足；Malmquist指数法适于面板数据，本文的数据为时间序列.因此，本文将借助生产函数法，即索洛残差法，对全要素生产率的变化进行测度.

索洛残差法的核心在于假定规模收益不变和希克斯中性技术满足，经济增长中扣除各投入要素贡献后的余额，即技术进步对经济增长的贡献，就是全要素生产率的变化率.

假定总量生产函数为C-D函数

其中，Yt为总产出，Kt为资本投入，Lt为劳动投入，At为满足希克斯中性的技术进步系数.根据规模收益不变的假定，α+β＝1.对(1)式两边分别取对数，并求关于时间t的导数.可得

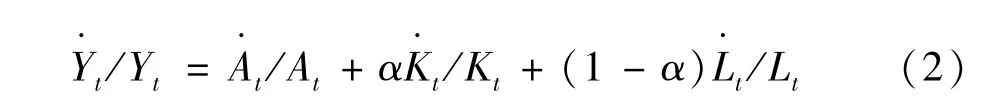
由(2)式，可得

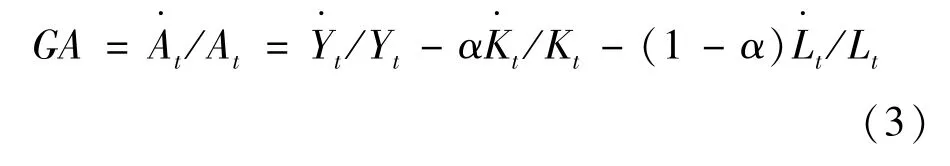
(3)式就是全要素生产率的变化率.

由(3)式可知，估算全要素生产率变化率的关键在于估计资本的边际贡献α.对(1)式两边分别除以L，并取自然对数.则有回归方程

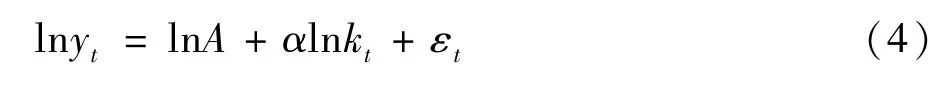
其中，yt＝ Yt/Lt为人均产出，kt＝ Kt/Lt为人均资本.同时，需要估算资本存量K，估算公式为：

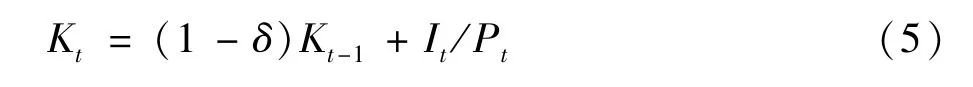
其中，Kt为第t年的资本存量，Kt-1为第t-1年的资本存量，Pt为固定资产投资价格指数，It为以第t年价格计量的固定资产投资，δ为折旧率.如此，可根据(5)式估算出各年的资本存量.

考虑到资本的边际贡献在所分析的样本期间内可能发生结构性变化，即资本对经济增长的贡献具有时变性，也就是说，α随时间发生变化，不是恒定的.基于此，把α看作一阶自回归过程，(2)式可变形为：

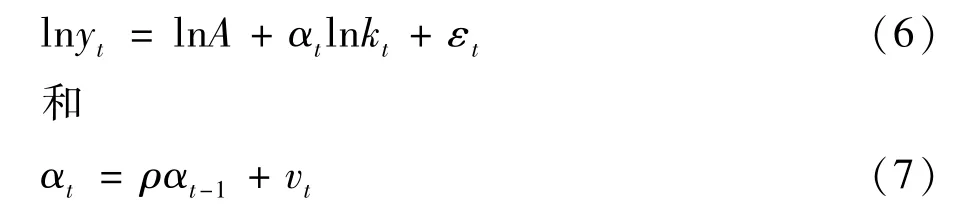
其中，ρ是自回归系数，v是白噪声过程.(6)式和(7)式组成了状态空间模型，(6)式是观测方程，(7)式为状态方程.利用极大似然法同时估计(6)和(7)式，可估算出资本的边际贡献序列αt.然后根据(3)式可测度出历年的全要素生产率变化率.

估算出全要素生产率变化率之后，就可借助协整检验模型验证创新驱动、教育发展与全要素生产率变化率之间是否存在长期均衡关系，并分析三者之间是否存在短期因果关系，利用脉冲效应描述三者之间相互影响的动态轨迹，最后，运用方差分解评价各内生变量对预测方差的贡献度.

2.2 数据来源

本文的研究期间为1978至2014年，总产出用国内生产总值(GDP)代表，劳动力指标取年初和年末就业人数的平均数，其数据均来自于各年的《中国统计年鉴》以及《新中国六十年统计资料汇编》，为了消除价格因素的影响，本文用1986年为基期的GDP平减指数对其进行平减处理.物质资本存量采用郭庆旺和贾俊雪(2005)的估算方法，折旧率取5%.教育发展指标的代表性因素较多，可使用财政性教育经费支出、人均接受教育年限、财政性教育经费占GDP和财政支出的比例等.由于财政性教育经费具有滞后性的特点，当年的财政性教育经费支出对经济增长的全部影响需要若干年后才能发挥出来.基于此，本文使用平均受教育年限作为替代性指标.该指标计算过程中所使用的数据来自于历年的《中国劳动统计年鉴》和《中国人口和就业统计年鉴》、《中国人口统计年鉴》和《中国统计年鉴》.创新驱动指标采用专利申请授权数替代，数据来自于历年《中国科技统计年鉴》.

3 统计分析

借助VAR模型，对创新驱动、教育发展与全要素生产率之间的长期动态均衡关系进行实证分析.在建立VAR模型之前，首先需要估算全要素生产率，然后对各变量的平稳性进行检验.如果所分析的变量是同阶单整的，进一步建立VAR模型，运用Johansen协整检验考察变量之间的协整关系，以此建立协整方程.最后在VAR模型的基础上，运用因果关系检验、脉冲响应函数和方差分解深入研究创新驱动、教育发展与全要素生产率变化之间的因果关系和动态影响过程.

3.1 全要素生产率变化率的测度

在估算全要素生产率变化率时，首先，根据(5)式估算出历年的资本存量，然后估计出生产函数和全要素生产率变化率.在估计生产函数时，需对规模收益不变的假设进行检验，同时，还需对生产函数的稳定性进行检验.利用Wald检验对无约束回归方程lnYt＝lnAt+αlnKt+βlnLt+εt中的假设α+β＝1进行验证，相应的F统计量的值为2.0929，伴随概率P值为0.1571，可知，P＞0.1，因此，在10%的显著性水平上，接受α+β＝1这一假设，即生产函数满足规模报酬不变.然后，对(4)式进行OLS回归，结果如下：

从回归结果可知，小括号内的 t统计量值为76.0079，以及中括号内的伴随概率P值为0.0000，P＜0.01，因此，在1%的显著性水平上，参数α是显著异于0的，也就是说lnkt对lnyt具有显著性影响，即物质资本每增长1%，产出将增长0.69%.接下来，借助CUSUM检验对参数α的恒定性进行检验，检验结果见图1.

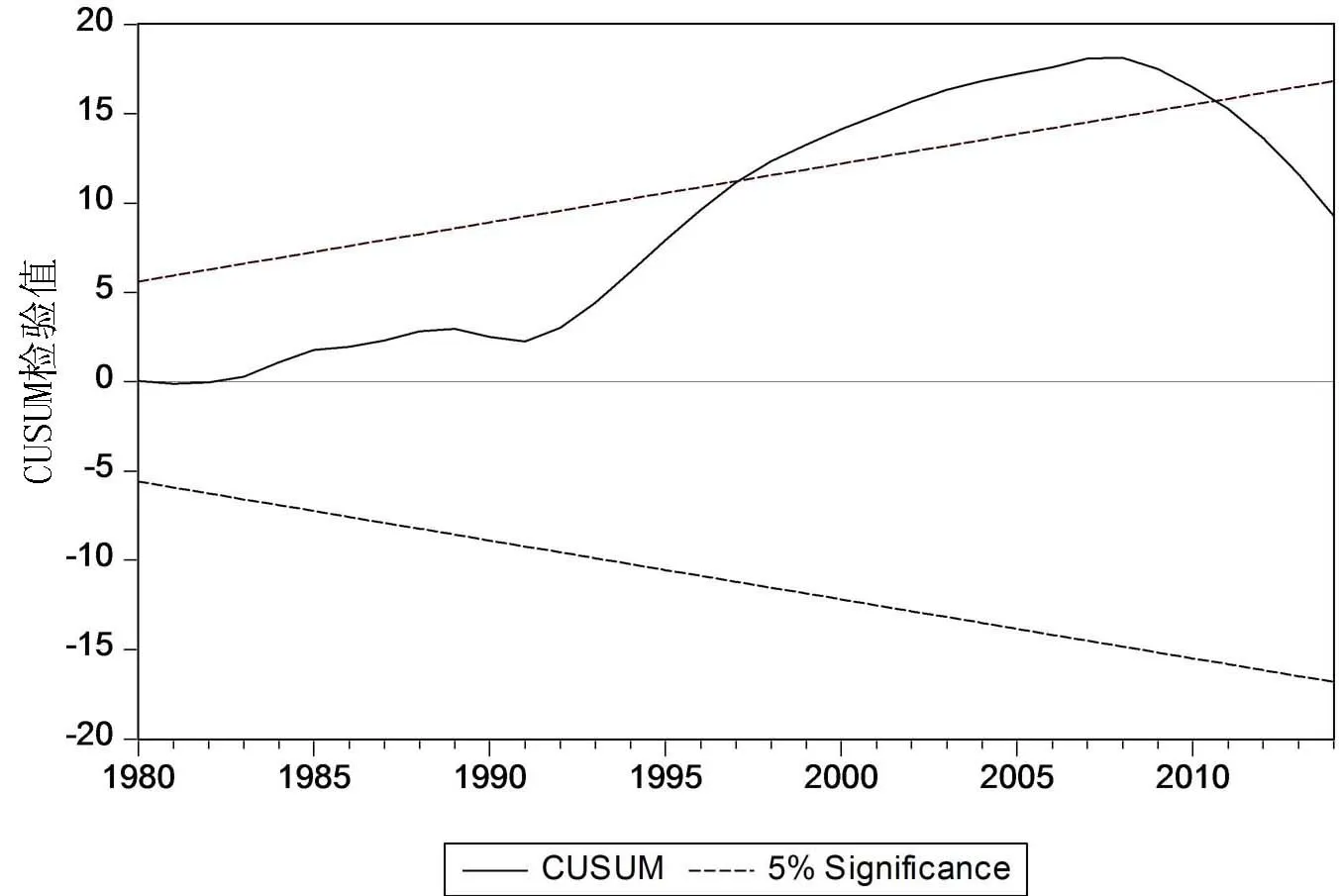
图1 模型稳定性的CUSUM检验

从图1可看出，在1997-2011年期间，生产函数的CUSUM检验值在5%的显著性水平上均超出了临界值边界(虚线表示)，这说明生产函数模型参数不恒定，具有随时间变化的趋势，需要建立可变参数状态空间模型对生产函数做进一步分析.最终，(6)和(7)式组成的状态空间模型的估计结果为：

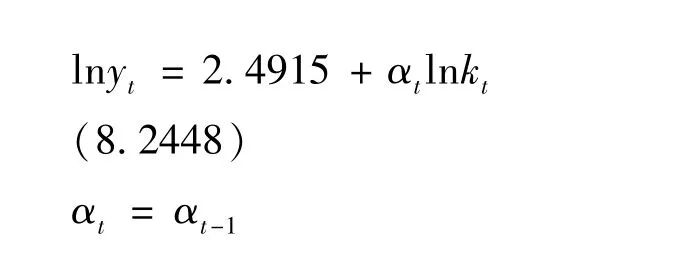
其中，括号内为t统计量值，从估计结果可知，资本的边际弹性αt是随机游走过程，其变化趋势见图2.

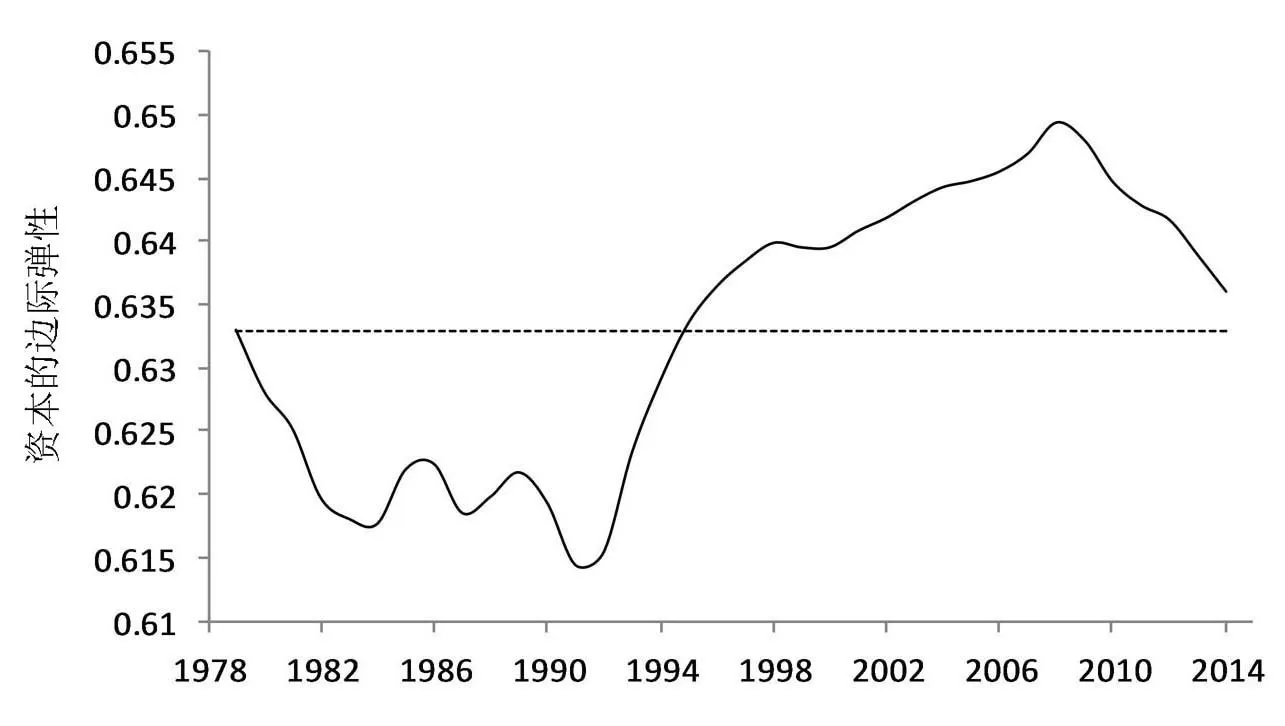
图2 资本的边际弹性αt序列的变化趋势

从图2可知，资本的边际产出弹性具有时变性(实线表示)，1979至1991年期间，总体上呈现下降趋势，1992至2008年期间，趋于上升，而2009-2014年，掉头向下.虚线部分表示的是1979至2014年期间这一弹性的平均值.

估算出资本的边际弹性αt之后，就可通过(3)式计算出全要素生产率变化率GA.该变化率序列的描 述性统计见表1.

表1 全要素生产率变化率的描述性统计

从表1可知，全要素生产率变化率处于-0.0433和0.0701之间，均值为-0.0019，中位数为0.0020，从中位数来看，全要素生产率增加率的幅度较小.

3.2 长期均衡关系

在获得了全要素生产率变化率序列之后，接下研究专利申请授权数、受教育年限和全要素生产率变化之间的长期动态关系.首先，对序列的平稳性进行检验，检验结果见表2.

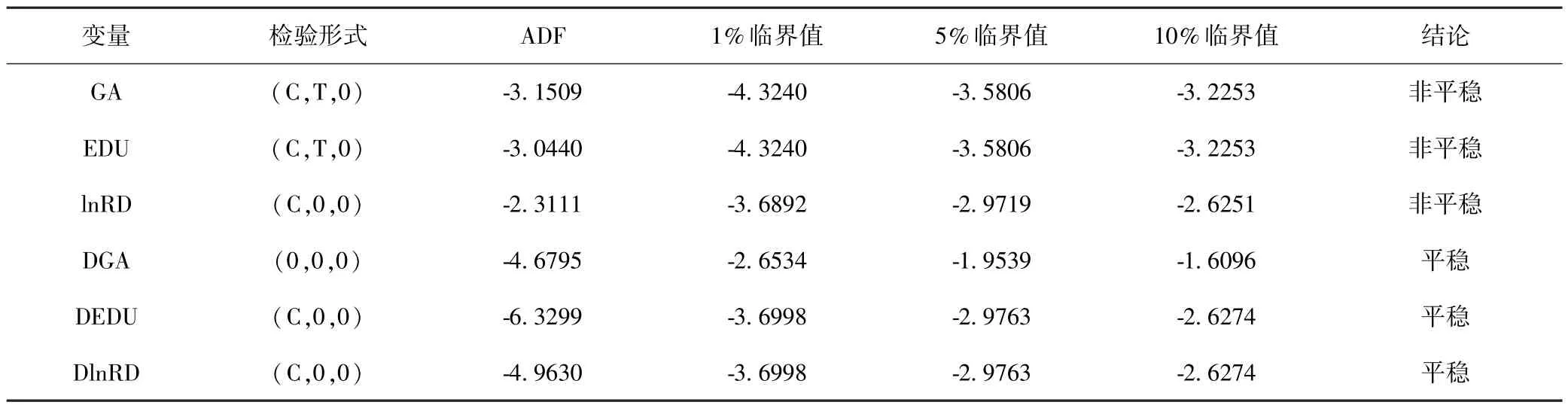
表2 ADF方法单位根检验结果

从表2可知，在10%的显著性水平上，全要素生产率变化率、受教育年限和专利申请授权数的原序列均是非平稳的，一阶差分后，各序列在1%的显著性水平上平稳，因而各序列均是一阶单整过程，即I(1).由于三个序列是同阶单整的，所以可对三个序列是否存在长期均衡关系进行验证，本文采用Johansen协整检验方法，检验结果见表3.

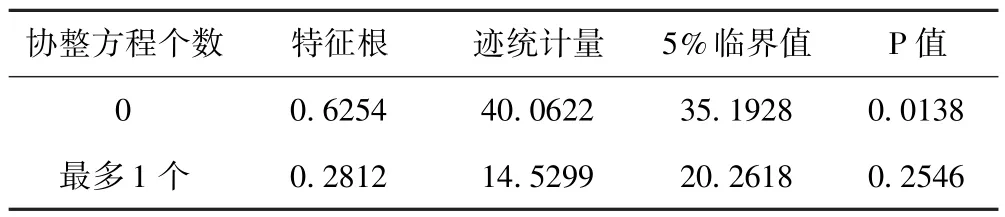
表3 协整检验结果

根据迹统计量和5%临界值的大小，可对协整方程个数进行判断.若迹统计量大于5%临界值，则拒绝原假设；若迹统计量小于5%临界值，则接受原假设.从表3可知，在5%的显著性水平上，存在一个协整方程.标准化的协整方程为：

从所估计的协整方程可知，专利申请授权数对全要素生产率变化的系数为0.1184，标准差为0.0303，受教育年限对全要素生产率变化的边际系数为-0.1711，标准差为0.0389.在5%的显著性水平上，专利申请授权数和受教育年限对全要素生产率变化的影响均显著.长期来看，专利申请授权数每增加1%，全要素生产率变化率将增加0.1184，相反，受教育年限每增加一年，全要素生产率的变化率将降低0.1711.

3.3 短期因果关系

协整检验的结果表明，专利申请授权数、受教育年限与全要素生产率变化之间存在长期动态均衡关系.然而，短期来看，三者之间会呈现何种互动.下面将借助Granger因果关系检验以验证三个变量之间是否存在短期因果关系，若存在，将进一步指出两个变量之间是否互为对方的Granger原因.检验结果见表4.

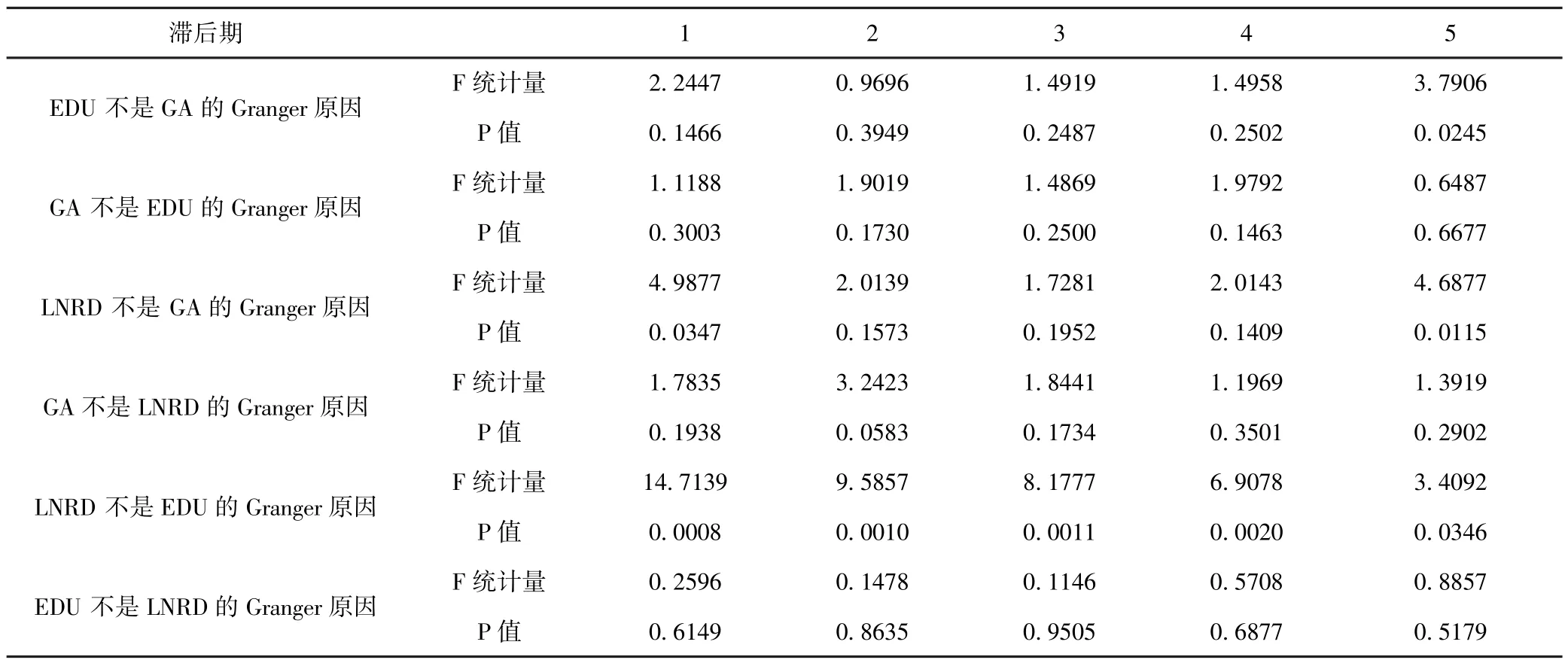
表4 因果关系检验结果

从表4可知，在滞后1期时，在5%的显著性水平上，只有专利申请授权数是全要素生产率变化的Granger原因；在滞后2期时，在10%的显著性水平上，全要素生产率的变化是专利申请授权数的Granger原因，这表明全要素生产率对专利申请授权数的反馈具有滞后性；在滞后5期时，专利申请授权数和受教育年限同为全要素生产率变化的Granger原因，受教育年限对全要素生产率变化的影响需要在更长的时间内才能显现；在所有的滞后期内，专利申请授权数均为受教育年限的Granger原因，这也验证了创新活动需要人力资本这一载体，人力资本的培养需要教育发展的支撑.

3.4 脉冲响应分析

协整检验和Granger因果关系检验的结果表明，专利申请授权数、受教育年限和全要素生产率变化之间不仅存在长期的动态均衡关系，而且具有短期的因果关系.然而，在由这三个变量组成的系统内，一个随机扰动项的变化会对系统内的变量产生何种程度的冲击，持续时间如何，接下来，运用VAR模型的脉冲响应对这一问题进行探讨.

脉冲效应函数描述的是变量的一个标准差随机扰动项的冲击对自身和其他变量的当期和未来期的影响轨迹，专利申请授权数、受教育年限和全要素生产率变化之间的脉冲响应函数见图3.

图3 专利申请授权数、受教育年限和全要素生产率变化之间的脉冲响应函数

从图3的左图可知，全要素生产率变化对自身一个标准差正向新息冲击的响应，在10个期间内始终为正，第2期达到最大，第4期处于最低，前4期波动较大，而后波动较为平稳；全要素生产率变化对专利申请授权数一个标准差正向新息冲击的响应，在第1期为零，第2至4期处于响应力度减弱阶段，随后两期趋于上升，第6期达到最大，第8期之后趋于稳定；全要素生产率变化对受教育年限一个标准差正向新息冲击的响应，第1期为零，第2和3期为正，此后响应一直为负.综合判断，全要素生产率变化对自身的冲击响应力度最强，专利申请授权数次之，且方向始终为正，对受教育年限的响应不仅强度最弱，而且，长期来看，方向为负.这表明创新驱动是全要素生产率变化的积极因素，而教育发展的增加并没有推动全要素生产率的提高，这与协整检验的结果一致.

从图3的中图可以看出，受教育年限对自身一个标准差正向新息冲击的响应，在第1期为正，且达到最大，而第2期就下降到零以下，此后一直为负，且波动较为平稳；受教育年限对专利申请授权数一个标准差正向新息冲击的响应，第1期为零，第2期为负，第3期及以后均为正，第4期之后趋于稳定，且响应力度较强；受教育年限对全要素生产率变化一个标准差正向新息冲击的响应，方向始终为负，且强度较弱.通过对图3的中图的描述，可以发现，创新驱动能够对教育发展产生持续的推动作用，这与因果关系检验的结论一致.

从图3的右图可以看出，专利申请授权数对自身一个标准差正向新息冲击的响应，强度较为稳定；面对全要素生产率变化一个标准差正向新息的冲击，专利申请授权数的反应强度较弱，方向始终为负；受教育年限一个标准差正向新息的变化，将对专利申请授权数产生持续的负向冲击，不过，相对专利申请授权数自身的冲击而言，力度稍弱.这充分说明创新驱动具有较强的惯性特征，其发展变化主要由自身推动，较少受其他两个因素的影响，这与因果关系检验的结论一致.

3.5 方差分解

脉冲响应函数描述了系统中每个内生变量的冲击对自身及其它变量影响的动态轨迹，而方差分解可以进一步评价各内生变量对预测方差的贡献度.通过方差分解，可比较相对重要性新息随时间的变化趋势，并能够估计该变量的影响程度与作用时滞.专利申请授权数、受教育年限和全要素生产率变化的方差分解结果见图4.

图4 专利申请授权数、受教育年限和全要素生产率变化之间的方差分解

从图4的左图可知，在全要素生产率的方差分解中，在滞后1期时，专利申请授权数和受教育年限对全要素生产率变化的冲击均为零，二者对全要素生产率的影响具有滞后性.专利申请授权数对全要素生产率变化的贡献持续增加，在第10期时达到最大，为17.46%.受教育年限对全要素生产率变化的贡献，在第5期达到最大，为5.85%，第7期之后趋于稳定，不过，贡献份额始终没有超过5%.这表明创新驱动对全要素生产率具有持续增加的推动作用，而教育发展的对全要素生产率变化的影响程度较小.

从图4的中图可以看出，在受教育年限的方差分解中，在滞后1期时，全要素生产率变化和专利申请授权数的冲击为零，二者对受教育年限的贡献具有一定的滞后性.专利申请授权数对受教育年限的贡献份额持续增加，且在第7期超过了受教育年限对自身的贡献，第10期时，这一贡献份额达到了46.99%.全要素生产率变化对受教育年限的冲击，前3期相对较小，而第4期增加幅度较大，由第3期的13.30%提高到21.45%，此后增加较为缓慢.这说明教育发展需要创新活动的驱动，教育与创新密切相关.

从图4的右图可以看出，在专利申请授权数的方差分解中，专利申请授权数对自身冲击的贡献在每期均在80%以上，全要素生产率变化对专利申请授权数的贡献在第1期最大，为12%，第2期降到5%左右，随后趋于稳定.受教育年限对专利申请授权数的贡献在前3期缓慢增加，第4期之后趋于稳定，并超过全要素生产率变化的贡献，但贡献份额始终较小.这说明现阶段创新驱动具有较强的惯性，较少受教育发展和全要素生产率变化的影响.

4 基本结论及建议

4.1 基本结论

本文首先对全要素生产率变化进行了估算，然后借助协整检验、因果关系检验、脉冲响应分析和方差分解，实证研究了创新驱动、教育发展与全要素生产率变化之间的关系，大体可以得到以下结论：

(1)资本的产出弹性具有时变性.从1978年至20世纪90年代初，资本的产出弹性趋于下降，然后，进入上升通道，至到2008年全球金融危机，随后，弹性降低.不过，在资本的产出弹性下降的同时，全要素生产率的增加率也趋于下降.

(2)创新驱动、教育发展与全要素生产率之间存在长期的动态均衡关系.创新驱动对全要素生产率的提高起到积极的促进作用，而教育发展对全要素生产率并没有起到预期的效果.

(3)创新驱动和教育发展均是全要素生产率变化的Granger原因，不过，教育发展发挥作用需要更长的滞后期，创新驱动也是教育发展的Granger原因.在全要素生产率变化的方差分解中，创新驱动和教育发展的贡献份额较低，不过，创新驱动的贡献在逐步增加.此外，创新驱动在教育发展的方差分解中逐步处于主导地位，成为推动教育发展的关键要素.

4.2 政策建议

根据研究结论，结合我国国情，给出相关政策建议：

(1)创新驱动对全要素生产率的提高具有显著的促进作用.这要求进一步推动“大众创业、万众创新”，使创新真正成为引领发展的第一动力，为全要素生产率的提高奠定最广泛的基础.

(2)加快推动高等教育的发展.在本文的实证研究部分，教育发展既没有对创新驱动产生积极的推动，也没有促进全要素生产率的提高.原因可能在于，本文以受教育年限作为教育发展的指标，在我国的人均受教育年限的构成中，初等教育占了较大比重，而高等教育的发展显得相对不足，高水平的全要素生产率需要高质量的人力资本，高质量的人力资本需要高等教育的培养.基于此，应进一步扩大高等教育的规模，为全要素生产率的提高供应源源不断的智力资源.