台阶式溢洪道水流压强特性试验研究

赵相航 解宏伟 郭馨 贺巨龙

摘要：为探讨台阶式溢洪道水流压强特性，结合青藏高原某水库，采用物理模型试验方法对高海拔地区台阶式溢洪道时均压强、脉动压强等特性进行了系统研究。结果表明：台阶式溢洪道水平面时均压强和脉动压强变化规律基本一致，从台阶凹角向凸角方向先有所减小，后逐渐增大，当流量较小时，时均压强在初始台阶会出现负值；台阶竖直面负压区范围超过整个台阶高度的一半，脉动压强在台阶顶角处较大；台阶式溢洪道时均压强和脉动压强沿程交替出现波峰和波谷，呈波浪状变化，总体上随流量的增大而增大，改变台阶尺寸，其值也发生变化；台阶式溢洪道脉动压强是随时间变化的平稳各态历经的随机过程，脉动优势频率为0～2Hz，属低频振动，其概率密度为偏态分布，不会危害泄水建筑物安全。

关键词：台阶式溢洪道；时均压强；脉动压强；高海拔地区

中图分类号：TV651.1 文献标志码：A doi：10.3969/ j.issn.1000-1379.2018.05.030

近几十年来，台阶式溢洪道因具有消能效果好、工程投资少、施工工期短等优点而广泛应用于各类中小型工程中。台阶式溢洪道泄槽段由一系列台阶组成，其水流多数为紊流，并在台阶内产生旋滚，主流与旋滚水流相互摩擦、剪切和混掺，显著增加了溢洪道的阻力作用，使水流能量大幅削减。台阶式溢洪道水流流场不稳定，水流紊动剧烈，紊流脉动压强加大了溢洪道的瞬时荷载，使台阶式溢洪道发生振动，而脉动产生的负压有可能加剧溢洪道空化与空蚀，直接影响水利工程的安全。台阶式溢洪道脉动压强变化具有周期性，其压强时大时小，往复作用于台阶面上，使台阶式溢洪道发生强烈振动，当水流脉动优势频率与台阶式溢流坝自振频率接近时，可能使泄水建筑物发生共振破坏[1]。

目前，台阶式溢洪道广泛应用于实际工程中，因此有必要深入研究台阶式溢洪道水流的压强特性。Sanchez J.M.等[2]测量了滑行水流台阶竖直面和水平面上的时均压强；田嘉宁等[3]研究了台阶式溢洪道时均压强的特性，得出了其沿程变化的规律；王均星等初步探讨了卡基娃水电站放空洞内阶梯泄槽底板的脉动压力特征，指出水舌冲击点处脉动压力对底板的影响不可忽视。为全面了解高海拔地区台阶式溢洪道的压强特性，结合青藏高原某水库，对台阶式溢洪道压强特性进行了系统研究，掌握了其分布规律和对台阶式溢洪道的影响。

1 模型设计

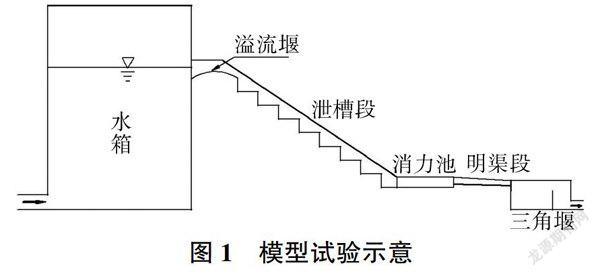
结合某水库实际工程，采用水工模型试验方法对高海拔地区台阶式溢洪道时均压强、脉动压强等特性进行研究。某水库坝面溢洪道位于坝体右岸一级阶地，由溢流堰、泄槽段、消力池和明渠段组成。溢流堰为实用堰型，采用开敞式正槽溢洪道段泄流，泄槽底坡为1：1.5。根据重力相似准则，运用正态模型设计，模型长度比尺Lr=40，材料为有机玻璃，泄槽段坡角θ=33.69°，高度为102.75cm，宽度为52.50cm，消力池长为50cm。试验对两种体型（台阶高h=3.00、2.07cm）台阶式溢洪道进行研究，单宽流量为0.0040～0.0228m3/（s·m），流量利用设在下游的三角形薄壁堰测量，并对一些典型流况进行拍照，模型试验示意见图1。

为观测台阶式溢洪道压强分布规律，沿模型宽度对称中心线布置测压孔，体型1（h=3.00cm）在台阶水平面和竖直面均布置3个测点，体型2（h=2.07cm）在台阶水平面和竖直面分别布置3个、2个测点，见图2。时均压强采用测压管测量，脉动压强采用中国水利水电科学研究院研制的DJ800系统进行数据采集和处理。试验采样频率为50Hz，采样间隔为0.02s，采样点数为4096，采样时间为81.92s。对采集数据运用Matlab仿真软件进行傅里叶变换，得到台阶式溢洪道底板压强脉动优势频率。

2 时均压强分析

2.1 台阶水平面时均压强分布

不同体型台阶式溢洪道水平面时均压强分布见图3（其中x/l为测点到台阶凹角的距离与台阶宽度的比值，q为单宽流量），从图3可以看出，台阶水平面时均压强在不同台阶高度下变化规律一致。时均压强变化趋势是从台阶凹角向凸角先有所减小，在距离台阶凹角大约0.25～0.40台阶宽度处出现一个较小值，其原因是台阶式溢洪道上覆主流受到台阶的阻碍在台阶内形成顺时针旋滚水流，当旋滚水流由水平面转向竖直面时，其运动方向背离台阶水平面，必将在水平面上产生一个压强较小点，凹角处因时均压强受台阶竖直面的阻碍而稍微偏高；随后，时均压强向外缘逐渐增大，表明台阶凸角处压强值较大，主要原因是台阶式溢洪道下泄水流受到台阶的限制，对水平面凸角处产生巨大的冲击，使凸角附近压强值增大。同时发现，台阶水平面时均压强总体上随上游来流量的增大而增大，主要原因是上游水位越高，水流惯性力越大，对台阶面时均压强影响越大。另外，改变台阶尺寸，台阶水平面凹角和中点处时均压强变化不大，凸角处时均压强变化明显；台阶高度降低，水流冲击作用减弱，凸角处时均压强随之减小。可见台阶式溢洪道水平面时均压强受上游来流量和台阶尺寸的影响。

2.2 台阶竖直面时均压强分布

不同体型台阶式溢洪道豎直面时均压强分布见图4（其中x/h为测点到台阶底角的距离与台阶高度的比值），从图4可以看出，体型1（h=3.00cm）时均压强沿台阶底角向顶角先逐渐减小，在距离台阶底角大约0.20～0.35台阶高度处开始出现负压，并在0.50台阶高度附近出现负压较小值；然后时均压强有所回升，但增幅不大。体型2（h=2.07cm）所设测点较少，只能看出时均压强沿台阶底角向顶角逐渐减小，在0.45-0.55台阶高度处出现负压。时均压强发生变化主要是旋滚水流在台阶内不断旋转、翻滚导致的；时均压强在台阶底角处因受旋滚水流的离心力作用而出现较大值；台阶内存在持续旋滚水流，空气不断被水体吸收，得不到外界补充，同时旋滚水流转向主流方向，背离台阶竖直面，使台阶内产生负压。同时发现，时均压强在台阶竖直面会形成负压区，上游来流量不同，负压区范围也不同；改变台阶高度，台阶竖直面开始出现负压的位置不同，台阶高度越小，负压区出现的位置越高。

2.3 时均压强沿程分布

通过分析台阶式溢洪道各测点时均压强可知，台阶式溢洪道台阶水平面凸角、中点和凹角处时均压强均呈波浪式发展，也就是说时均压强每隔几个台阶就会出现极大值和极小值，交替出现波峰和波谷，说明台阶水平面时均压强沿程变化规律具有起伏性。台阶式溢洪道台阶高度h=3.00cm和h=2.07cm的台阶凸角处时均压强沿程分布见图5（其中X/L为测点到台阶起点的水平距离与台阶水平长度的比值），从图5可以看出，体型相同时，随着上游来流量的增加，水流的惯性作用增强，沿程时均压强呈增大趋势，波动幅度也随之增大。改变台阶尺寸，台阶上时均压强交替出现极大值和极小值的幅度发生变化；台阶高度降低，台阶内旋滚区域缩小，过水断面尺寸变小使得水流失重减小，旋滚强度减弱，水流对台阶的冲击作用减小，时均压强随之减小。同时发现，在体型1单宽流量q=0.0043m3/（S·m）时，初始台阶位置出现负压，这主要是流量过小时产生挑射水流所致。试验结果表明，在台阶段时均压强波谷和负压区，水流空化数相对较小，应对其局部结构进行优化。

3 脉动压强分析

脉动压强常以均方根值表示，它表示了水流脉动压强偏离其数学期望值的程度，并反映水流脉动过程式中：pi'为i点脉动压强净为平均压强。

采集台阶式溢洪道底板脉动压强随时间的变化值可以发现，台阶式溢洪道底板脉动压强随时间的变化是一个随机过程，在上游来流量恒定的情况下，测量过程可以看作是平稳各态历经的随机过程。同时发现，由于台阶凸角处水流紊动剧烈，因此脉动压强变化幅度较大。体型1单宽流量q=0.0228m3/（S·m）時台阶式溢洪道脉动压强波形见图6。

3.1 台阶水平面脉动压强分布

不同体型台阶式溢洪道水平面脉动压强分布见图7，从图7可以看出，在台阶水平面上，脉动压强变化规律与时均压强的相似，即从台阶凹角向凸角先有所减小，在距离台阶凹角大约0.3～0.4台阶宽度处出现较小值，随后逐渐增大。在台阶水平面凸角处，下泄水流直接冲击在台阶上，发生强烈碰撞，因台阶的限制而发生转向，并在台阶内形成高速旋滚水流，旋滚水流与主流之间发生强烈的紊动剪切作用，水流紊乱加剧，脉动压强增大；在距离台阶凹角大约0～0.5台阶宽度处水流为旋滚水流，受上覆主流影响较小，水流流态相对稳定，该范围内脉动压强变化不大；台阶凹角处小旋滚的存在增强了自身紊乱作用，脉动压强有所增大。由此可见，台阶水平面脉动能量主要集中在台阶凸角水舌跌落处。从图7还可以看出，台阶水平面脉动压强总体上随着上游来流量的增大而增大，其原因是随着上游来流量的增大，下泄水流流速增大，水股逐渐增厚，水流对台阶面的冲击作用增强，水流之间的紊动剪切加剧，脉动压强随之增大。另外，改变台阶尺寸，台阶水平面脉动压强发生变化，台阶高度降低，凸角处脉动压强减小。可见台阶式溢洪道水平面脉动压强受上游来流量和台阶尺寸的影响。

3.2 台阶竖直面脉动压强分布

不同体型台阶式溢洪道竖直面脉动压强分布见图8，从图8可以看出，台阶竖直面脉动压强沿凹角到中点变化不大，图8（a）中脉动压强沿中点向顶角逐渐增大，图8（b）受测点少的限制无法看到台阶上部压强变化。在台阶顶角处，受上一级台阶水流冲击的影响，上覆水流变得紊乱，同时台阶内旋滚水流在顶角处发生转向，其旋转方向与上覆主流流向一致，发生强烈的紊动剪切和混掺，水流紊动剧烈，脉动压强较大。从图8（a）可以看出，顶角处脉动压强随上游来流量的增大呈增大趋势，主要原因是随着下泄水流流量的增大，主流和旋滚水流流速增大幅度不同，内部剪切加剧，另外受水流冲击作用增强，水流流态变得极其紊乱，促使顶角处脉动压强增大。改变台阶尺寸，台阶竖直面脉动压强有所改变。

3.3 脉动压强沿程分布

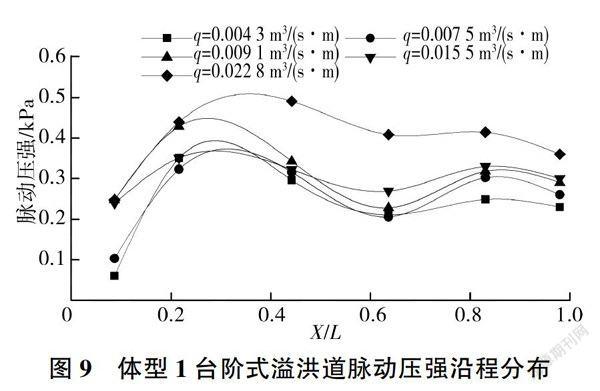
台阶式溢洪道脉动压强沿程分布研究表明，台阶各测点脉动压强在不同流量时呈现出相同的变化规律，即沿程交替出现波峰和波谷，呈波浪状分布。台阶凹角和中点处脉动压强因受台阶内水体的削弱作用而变化较小，沿程波动幅度不大，其分布也相对均匀；台阶凸角处脉动压强较大，沿程波动幅度相对明显。另外，脉动压强受上游来流量的影响较大，总体上随上游来流量的增大而增大，但对其波动幅度影响不明显。体型1台阶式溢洪道凸角处脉动压强沿程分布见图9。

3.4 频谱分析

对于台阶式溢洪道水气两相流来说，当上游来流量一定时，脉动压强变化是一个平稳各态历经的随机过程。功率谱密度表示不同频率结构分量组成脉动压强的平均能量值[9]，通过频谱分析，可以了解脉动的频率结构、能量分布、脉动强弱等压强脉动特性，并得到频谱密度最大时对应的优势频率。当台阶式溢洪道优势频率与大坝自身的自振频率接近时，将产生共振现象，使泄水建筑物发生破坏。对台阶式溢洪道频谱分析可知，台阶式溢洪道各测点优势频率分布在0～2Hz，优势频率为低频，频带较窄，受大涡体紊动惯性作用影响较大，这与台阶式溢流坝自振频率相差较大，一般不会对泄水建筑物造成共振破坏。

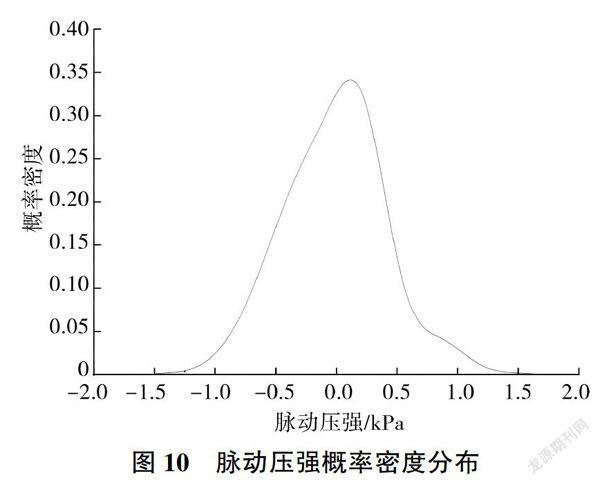
为了解台阶式溢洪道水流脉动压强随机信号的正态性，对台阶式溢洪道各测点脉动压强概率密度分布进行了研究。研究表明，台阶式溢洪道脉动压强概率密度不是标准的正态分布，而是偏态分布，但在实际工程中可以看成正态分布[10]。体型1台阶7凸角处脉动压强概率密度分布见图10。

4 结语

采用水工物理模型试验方法，对高海拔地区台阶式溢洪道压强特性进行了研究，试验结果表明：台阶水平面时均压强和脉动压强变化规律一致，从台阶凹角向凸角先逐渐减小，后逐渐增大，凸角处受水流冲击影响严重，应加强防护；台阶竖直面负压区范围超过整个台阶高度的一半，负压范围较大，易发生空化破坏；台阶竖直面凹角和中点处脉动压强相差不大，从中点向顶角逐渐增大；台阶式溢洪道时均压强和脉动压强沿程呈波浪状变化，交替出现波峰波谷，且总体上随上游来流量的增大而增大，改变台阶尺寸，其值也发生变化；当流量较小时，时均压强在初始台阶出现负值；台阶式溢洪道水流脉动过程属于平稳各态历经的随机过程，水流脉动优势频率为0～2Hz，属低频振动，其概率密度分布为偏态分布，不会对泄水建筑物造成共振破坏。该工程位于青藏高原地区，研究成果可为高海拔地区类似工程的优化设计提供参考。

参考文献：

[1]李静，姜伯乐，金峰.消力池底板及导墙脉动压力特性试验研究[J].人民长江，2009，40（17）：52-54.

[2]SANCHEZ J M，POMARES J，DOLZ J.Pressure Field inSkimming Flow Over a Stepped Spillway[C]//Proceeding ofthe International Workshop on Hydraulics of Stepped Spill-ways.Switzerland：A，A，Balkema，2000：137-145.

[3]田嘉宁，魏炳乾，李布雳，等.台阶式溢流坝的时均压强特性[J].水力发电学报，2007，26（6）：67-72.

[4]王均星，杜少磊，陈利强，等.卡基娃水电站放空洞脉动压力模型试验研究[J].武汉大学学报（工学版），2012，45（4）：436-441.

[5]中华人民共和国水利部.水工（常规）模型试验规程：SL155-2012[S].北京：中国水利水电出版社，2012；1-21.

[6]刘安富，杨敏，李会平，等.宽尾墩消力池透水底板脉动压力试验研究[J].水科学进展，2012，23（2）：243-248.

[7]任雨，王承恩，刘斌.阶梯式溢洪道水平面上时均压强试验研究[J].人民黄河，2011，33（3）：123-124.

[8]曾东洋.台阶式溢洪道水力特性的试验研究[D].西安：西安理工大学，2002：53-54.

[9]张微，陈锐，王玥.过水围堰混凝土面板水流脉动压力试验研究[J].水电能源科学，2012，30（1）：145-148.

[10]郑阿漫.掺气分流墩台阶式溢洪道水力特性的研究[D].西安：西安理工大学，2001：45-50.