基于Fibonacci-Lucas序列构造大围长QC-LDPC码的方法

袁建国，曾 晶,袁 梦，范福卓，刘家齐，郑德猛

(重庆邮电大学 光通信与网络重点实验室，重庆 400065)

0 引 言

生活在当今信息时代，人们在许多领域如政治、经济、军事、科技方面都需要可靠有效地传输信息，现代的数字通信系统基本上都使用了信道纠错编码技术。低密度奇偶校验(low-density parity-check, LDPC)码是一种误差纠正技术，可适用于不同信道范围。LDPC码应用十分广泛，诸如无线局域网通信、深空宇航通信、数字水印技术、磁性记录信道、超高速光纤传输等[1]，其实际意义和经济价值很大。

根据LDPC码特点，能从不同的角度进行分类，结构化构造和随机构造就是按照其校验矩阵的特性进行分类，渐进边增长(progressive edge growth, PEG)构造法是随机构造中的一种，为了增加其Tanner图的边而采用计算机搜寻方式，正由于其校验矩阵的随机可变，并且有着高的计算复杂度，所以实践中应用并不广泛。而结构化构造LDPC码，对比于随机构造，复杂度低出很多，同时十分有利于实践应用，因而受到广泛关注[2-4]。准循环LDPC (quasi-cyclic LDPC, QC-LDPC)码是一种由单位矩阵循环置换后的矩阵构成的阵列，仅仅需要数量较少的存储器存储它们的奇偶校验矩阵，它们的结构性质比随机性更加容易分析,它们能在实践中方便简单的实现[5-7]。LDPC码Tanner图的周期结构对纠错性能有很大影响，其Tanner图中最小环长称为围长，由于小围长会使得译码过程中信息在迭代之后互相关，影响到了译码收敛性能[8-10]，因此，自LDPC研究以来，就有大量的工作投入用于设计较大围长的LDPC码[11]。

本文基于斐波那契-卢卡斯序列并结合文献[12]中三角旋转法构造出的QC-LDPC码，计算复杂度低且不存在四环和六环，硬件实现简单，经Matlab软件仿真后，进行对比分析，表明该码字性能比基于Fibonacci数列并结合三角旋转法构造出来的QC-LDPC码更好，同时也好于基于卢卡斯数列无四六环构造方法构造出来的QC-LDPC码[13]和基于等差数列(arithmetic progression sequence, APS)构造的QC-LDPC码。

1 斐波那契-卢卡斯序列简介

1.1 斐波那契-卢卡斯序列的定义

斐波那契序列定义：数列F(n)分布形式如0，1，1，2，3，5，8，13，21，34，…，其中,n≥0，n∈N，F(0)=0，F(1)=1，则Fibonacci序列被如下递归方式定义为F(n)=F(n-1)+F(n-2)(n≥2,n∈N)。

卢卡斯序列定义：数列L(n)分布形式如2,1,3,4,7,11,18,29,47,…,其中,n≥1，n∈N*，L(1)=2，L(2)=1，则Lucas序列被如下递归方式定义为L(n)=L(n-1)+L(n-2)(n≥3,n∈N)。

斐波那契-卢卡斯序列定义：递增数列F(n)分布形式如1,3,4,7,11,18,29,47,…，其中,n≥0，n∈N，F(0)=1，F(1)=3，Fibonacci-Lucas序列被如下递归方式定义为F(n)=F(n-1)+F(n-2)(n≥2,n∈N)。

1.2 Fibonacci-Lucas序列定理

定理1对于整数数列F(n)，f(n)为数列中第n个数的数值，若m>n，且m,n,k∈N*有f(m+k)-f(m)>f(n+k)-f(n)[14]。

根据Fibonacci-Lucas序列中数字的特性结合三角旋转法，得到一种围长为8的QC-LDPC码。

2 基于斐波那契-卢卡斯序列的QC-LDPC码构造方法

2.1 基于斐波那契-卢卡斯序列并结合三角旋转法构造QC-LDPC码

步骤1把斐波那契-卢卡斯序列按照如下三角形结构放置，其中，行数i=1,2,3,…，参数r的取值影响着码长的变化，为了得到长码长则r取较大值，反之得到短码长则r取较小值，其中r∈Z+。

i=1F(1+1+r)+1

i=2F(2+2+r)+2F(2+1+r)+2

i=3F(3+3+r)+3F(3+2+r)+3F(3+1+r)+3

iF(2i+r)+iF(2i-1+r)+i…F(i+1+r)+i

步骤2逆时针旋转45°为

i=1F(1+1+r)+1F(2+1+r)+2F(3+1+r)+3…

i=2F(2+2+r)+2F(3+2+r)+3F(4+2+r)+4…

i=3F(3+3+r)+3F(4+3+r)+4F(5+3+r)+5…

i=4F(4+4+r)+4F(5+4+r)+5F(6+4+r)+6…

步骤3基于以上形式，构造出一个指数矩阵E(H)，E(H)的维数为J×L。F(0)为1占满了指数矩阵第一行，其后所有行所构成的矩阵形式即为45°旋转后所得到的矩阵。于是，指数矩阵为

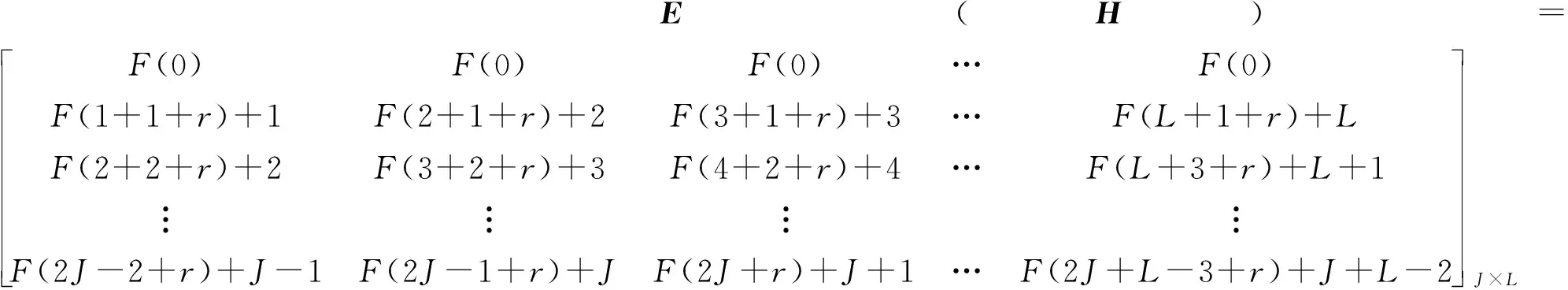
(1)

从(1)式中可看出，指数矩阵E(H)中元素均为正整数；除第一行元素全为F(0)外，其余每行都是递增数列。令0≤i≤J-1，0≤s≤L-1，E(H)中任意一个元素可表达为

E(i,s)=F(2i+s+r)+i+s

(2)

步骤4根据构造出来的指数矩阵E(H)，为了能充分利用码长来进一步优化，引入参数k，替换E(H)中尾部元素为E(i,s)+k(k∈N)，使其逼近维数P，再用维数为P×P的单位矩阵循环移位后得到的矩阵去代换E(H)中各元素，其中，循环移位数即指数矩阵E(H)中对应元素，扩展因子P即单位矩阵维数，需满足表达式：P≥F(2J+L-3+r)+J+L-1+k，于是，校验矩阵H的构造如(3)式所示。

(3)

循环置换子矩阵维数可连续取值，扩展后的校验矩阵维数为JP×LP。

2.2 围长至少为8的性质证明

首先，定义y(i,s)为指数矩阵中第i行，第s列的元素，其中，0≤i≤J-1,0≤s≤L-1且i,s∈N。QC-LDPC码中存在的2K环可以用表达式表达为y(i0,s0)，y(i0,s1)，y(i1,s1)，…，y(ik-1,sk-1)，y(ik-1,s0)，y(i0,s0)。为了使得基于Fibonacci-Lucas序列并结合三角旋转法构造QC-LDPC码无2K环，则应使得(4)式成立。即

(4)

(4)式中：iv≠iv+1；sv≠sv+1。

从2个方面分别进行说明，无四环及无六环。

不存在四环证明：根据(4)式可知要得到无四环即使得(5)式成立，即

y(i0,s0)-y(i1,s0)+y(i1,s1)-y(i0,s1)≠0 modp

(5)

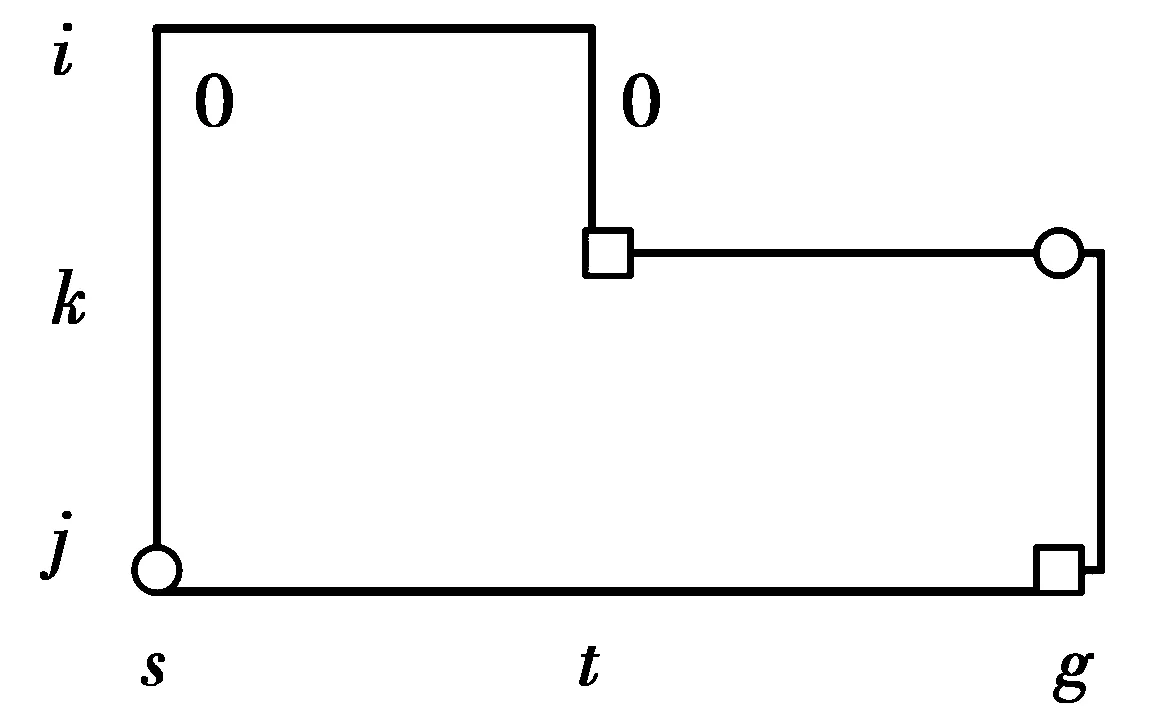
令i0

y(i0,s0)-y(i1,s0)+y(i1,s1)-y(i0,s1)=

F(2i0+s0+r)+i0+s0-(F(2i1+s0+r)+i1+s0)+

F(2i1+s1+r)+i1+s1-(F(2i0+s1+r)+i0+s1)

由定理1可推得

F(2i1+s1+r)+i1+s1-(F(2i1+s0+r)+i1+s0)>

F(2i0+s1+r)+i0+s1-(F(2i0+s0+r)+i0+s0)，

0

由上式推导可知构造的校验矩阵无四环的存在。

无六环证明：在Tanner图中，六环存在的形式有6种如图1所示。

图1 六环的6种形式Fig.1 Six pattern of the girth-6

可将图1中6种六环结构分为2类：①图1所示的前4种形式，若已推得其中一种形式，另外3种则可由其变形推导而得；②图1所示后2种形式，也可以相互变形推导。因此，每一类只需推导其中一种形式即可。

根据(4)式可知要得到无六环即需(6)式成立，即

y(i,s)-y(i,t)+y(j,t)-y(j,g)+

y(k,g)-y(k,s)≠0 modp

(6)

对于图1第1类，当i=0时可能出现如图2所示的情形，下面证明图2中六环第1类中的第1种形式，其他情况同理可推得。

由(2)式和(6)式可得

y(i,s)-y(i,t)+y(j,t)-y(j,g)+y(k,g)-y(k,s)=

1-1+F(2j+t+r)+j+t-(F(2j+g+r)+j+g)+

F(2k+g+r)+k+g-(F(2k+s+r)+k+s)=

F(2j+t+r)+j+t-(F(2j+g+r)+j+g)+

F(2k+g+r)+k+g-(F(2k+s+r)+k+s)

图2 六环的形式一Fig.2 Type-1 of the girth-6

令s=g-m,t=g-n且m>n，则上式可化为

y(i,s)-y(i,t)+y(j,t)-y(j,g)+y(k,g)-y(k,s)=

F(2j+g-n+r)+j+g-n-(F(2j+g+r)+j+g)+

F(2k+g+r)+k+g-(F(2k+g-m+r)+k+g-m)=

F(2j+g-n+r)-n-F(2j+g+r)+

F(2k+g+r)-(F(2k+g-m+r)-m)

(7)

又由定理1可得

F(2k+g+r)-(F(2k+g-m+r)-m)>F(2j+g+r)-

(F(2j+g-n+r)-n)

则：0<(7)式

当i≠0：

y(i,s)-y(i,t)+y(j,t)-(y(j,g)+y(k,g)-y(k,s))>

y(i,s)-y(i,t)+y(j,t)-(y(j,g)+y(j,g)-y(j,s))=

y(i,s)-y(i,t)+y(j,t)-y(j,s)>0

y(i,s)-y(i,t)+y(j,t)-(y(j,g)+y(k,g)-y(k,s))<

y(k,s)-y(i,t)+y(j,t)-(y(j,g)+y(k,g)-

y(k,s))=y(j,t)-y(i,t)+y(k,g)-y(j,g)<

y(j,g)+y(k,g)-y(j,g)=y(k,g)

夹逼定理定义：F(x)与G(x)连续且存在同样的极限Α，即x→X0时，limF(x)=limG(x)=Α，则若函数f(x)在X0的某邻域内，恒有F(x)≤f(x)≤G(x)，则当x趋近X0，有limF(x)≤limf(x)≤limG(x)即Α≤limf(x)≤Α，故limf(X0)=Α。

根据夹逼定理可以得到：原式≠0 modp。

对于图1第2类中第1个形式，当i=0：

y(i,s)-y(i,t)+y(k,t)-(y(k,g)+y(j,g)-

y(j,s))=1-1+F(2k+t+r)+k+t-(F(2k+g+r)+

k+g)+F(2j+g+r)+j+g-(F(2j+s+r)+j+s)=

F(2k+t+r)+k+t-(F(2k+g+r)+k+g)+

F(2j+g+r)+j+g-(F(2j+s+r)+j+s)

令s=g-m,t=g-n且m>n，则上式可化为

y(i,s)-y(i,t)+y(k,t)-(y(k,g)+y(j,g)-y(j,s))=

F(2k+g-n+r)-n-F(2k+g+r)+

F(2j+g+r)-(F(2j+g-m+r)-m)

(8)

由定理1可推得

F(2j+g+r)-(F(2j+g-m+r)-m)<

F(2k+g+r)-(F(2k+g-n+r)-n)

则：-P<(7)式<0，即原式≠0 modp。

当i≠0：

y(i,s)-y(i,t)+y(k,t)-(y(k,g)+y(j,g)-y(j,s))<

y(j,s)-y(j,t)+y(k,t)-(y(k,g)+y(j,g)-y(j,s))=

y(j,g)-y(j,t)+y(k,t)-y(k,g)<0

y(i,s)-y(i,t)+y(k,t)-(y(k,g)+y(j,g)-y(j,s))>

y(i,g)-y(j,t)+y(k,t)-y(k,g)>y(k,t)-y(k,g)>-p

根据夹逼定理可以得到：原式≠0 modp。

由以上分析可得，6种六环形式是不可能出现的，所以，当P≥F(2J+L-3+r)+J+L-1时，无四环及六环，围长至少为8的性质得以证明。

3 仿真性能分析

基于斐波那契-卢卡斯序列结合三角旋转法构造出1个QC-LDPC码，列重为J=3，行重L=6，参数r=2，其指数矩阵为

(9)

P的取值为：P≥E(J-1,L-1)+1=430，本文选择P=450和P=430，那么码长分别为2 700和2 580。最终可分别得到行重为6，列重为3，码率为0.5的F-LQC-LDPC(2 700,1 352)码和F-L-QC-LDPC(2 580,1 292)码。

基于斐波那契-卢卡斯序列并结合三角旋转法构造的QC-LDPC码，对其使用Matlab软件进行仿真，设置在白色高斯信道，同时进行二进制相移键控调制，且使用BP译码算法，译码迭代次数选取为50次，再将F-L-QC-LDPC码仿真图分别与同码长同码率基于Fibonacci序列结合三角旋转法构造出来的QC-LDPC码、基于卢卡斯数列构造的无四六环QC-LDPC码和基于等差数列构造的QC-LDPC码进行对比分析，如图3所示。

由图3分析可知，在BER为10-6时，基于Fibonacci-Lucas序列并结合三角旋转法构造的F-L-QC-LDPC(2 700,1 352)码相较于文献[12]中基于Fibonacci数列并结合三角旋转法构造的同码长同码率F-QC-LDPC(2 700,1 352)码，围长增大到至少为8，净编码增益改善了大约1.0 dB，相较于文献[13]中使用卢卡斯序列填充指数矩阵构造的同码长同码率L-QC-LDPC(2 700,1 353)码，虽然同样避免了四六环，但Fibonacci-Lucas序列同时巧妙结合了三角旋转法使得其他码比特对信息计算提供了更大的帮助，提高了纠错性能，净编码增益改善了大约1.6 dB，同样在BER为10-6时，基于Fibonacci-Lucas序列并结合三角旋转法构造的F-L-QC-LDPC(2 580,1 292)与文献[9]中基于等差数列构造的APS-QC-LDPC(2 580,1 292)码相比，净编码增益提高了约1.0 dB。从编码复杂度角度来看，可从2个方面进行分析，一个是运算复杂度；另一个是编码所需存储的参数，其中，运算复杂度是运算量和码长的变化关系。本文提出的构造方法相比于文献[12]中基于Fibonacci数列构造的F-QC-LDPC码和文献[13]中使用卢卡斯序列构造的L-QC-LDPC码具有相同码长和码率，且都是通过生成矩阵进行编码，运算量均与码长的平方呈线性关系，因此，运算复杂度一样大。而本文提出的构造方法，其指数矩阵尺寸为J行L列，其中第一行全为元素1，因此，所需存储的参数为(J-1)×L+1个，与文献[12]和文献[13]中构造J行L列指数矩阵对比，所需存储参数个数相同，从编码复杂度来看三者一样。综合分析可得，本文提出的构造方法与文献[12]和文献[13]中构造方法对比，在复杂度相同的情况下，纠错性能得到改善。

图3 F-L-QC-LDPC码与其他码的纠错性能仿真图Fig.3 Simulation diagram of the error-correction performance among theF-L-QC-LDPC code and other codes

4 结 论

基于Fibonacci-Lucas序列并结合三角旋转法构造QC-LDPC码，能避免四环和六环的产生，有较好的纠错性能，循环置换子矩阵维数可连续取值，另外设置相应的参数可得到不同的码长和码率。用此构造方法构造的F-L-QC-LDPC码，仿真结果表明，其纠错性能优于基于Fibonacci序列结合三角旋转法构造的同码长同码率F-QC-LDPC码也同样优于使用卢卡斯序列填充指数矩阵的同码长同码率L-QC-LDPC码和基于等差数列构造的APS-QC-LDPC码。