非严格递增作业速度的斗链装配线自平衡特性
2018-09-08刘俨后左敦稳李学伟
刘俨后,麻 娟,左敦稳,李学伟,3
(1.山东理工大学 机械工程学院,山东 淄博 255000;2.南京航空航天大学 机电学院,江苏 南京 210016; 3.西安瑞特快速制造工程研究有限公司,陕西 西安 710000)
1 问题的提出
Bucket Brigades是一种采用walking-worker的生产组织形式,中文文献一般称之为斗链,其基本规则为:
规则1工人按固定顺序排列且不允许超越,工人与工件同步移动的同时完成作业,直到下游工人接手其工件(或到达末端)。
规则2完成作业的工人返回上游工人处接手工件(或从始端领取任务)。
斗链的示意图如图1所示,其中wj(j=1,2,…,n)表示在线工人,xj表示工人wj的位置。斗链最早由Bartholdi和Eisenstein开始研究,其研究基于以下约束:①工人为异质员工,按照作业速度由慢到快递增排列;②由于工件交接和回取耗时比作业时间小得多,回取速度和交接时间忽略不计;③作业均匀连续分布在生产线上,交接可在任意位置进行[1]。基于上述约束,Bartholdi等[1]建立了一个标准斗链(Normative Bucket Brigades, NBB)模型,并证明NBB具有自平衡性。

在NBB的基础上,国内外诸多学者对斗链展开了研究。Bartholdi等[2-3]分析了随机斗链的自平衡特性和生产效率,并针对分支装配线设计了一种作业共享机制;Bratcu等[4-5]结合实际案例,采用混合动态系统理论分析斗链的平衡性,并基于MATLAB进行建模与仿真;Armbruster等[6-7]针对工人差异,建立改进模型以提高生产效率,并研究了工人学习能力对斗链性能的影响;Song等[8]通过优化工人指派进行斗链的自平衡研究;Lim[9]和Quader等[10]对双向作业斗链进行研究,保证工人在回走阶段也能有效作业;Manzini等[11]和Hong等[12]将斗链应用于物流配送仓储的拣货系统;Chen等[13]在斗链中引入工人超越机制,以提高生产效率。目前国内的相关研究较少,徐翔斌等[14]对斗链进行研究综述及应用前景展望;彭勇等[15]研究了回取速度与工件交接位置的关系,证明回取速度越小,交接位置偏离越大;廖世龙等[16]提出一种带有超越站的超越机制,以提高产能;刘俨后等[17]根据工位约束条件的不同,对斗链的平衡点特性进行了对比研究。
上述研究多针对约束②或考虑超越机制进行研究,文献[17]针对约束③进行了研究,目前尚未有针对约束①的相关文献。在真实车间环境中,很难对个体作业速度进行衡量和评价,作业速度或作业时间一般通过车间数据统计给出,约束①很难严格满足。因此在实际生产中,管理决策更多的是针对作业速度相同的同质员工进行。为此,在释放NBB的约束条件①的基础上,本文对非严格递增作业速度的斗链装配线(Bucket Brigades Assembly Line, BBAL)进行建模与仿真研究,并进一步提出同质员工BBAL的有效运行规则。
2 问题描述
有n个工人{wj|j=1,2,…,n}的BBAL如图1所示。若定义一个基准作业速度v0,则wj的作业速度可记为vj=λjv0(j=1,2,…,n),其中λj≥1为作业速度系数,NBB满足约束①,即λ1<λ2<…<λn。若作业速度系数满足λ1≤λ2≤…≤λn,且至少存在一个“=”,则称作业速度非严格递增排列,本文根据约束①的满足程度,将BBAL分为标准斗链装配线(Normative Bucket Brigades Assembly Line, NBBAL)和非严格递增斗链装配线(Non-Strictly increasing Bucket Brigades Assembly Line, NSBBAL)两类,其中NSBBAL又分为NSBBAL-E和NSBBAL-C,具体定义如表1所示。

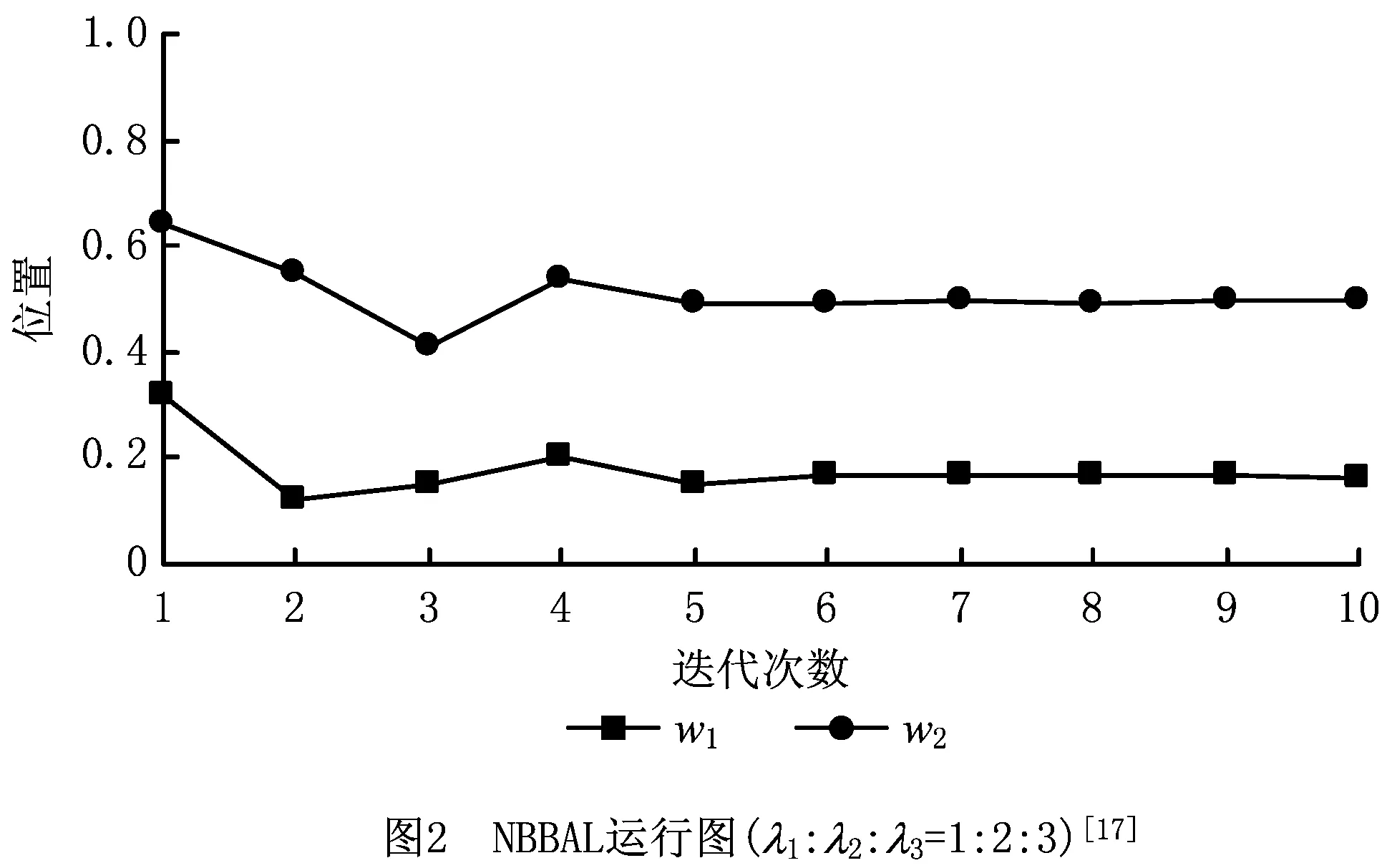
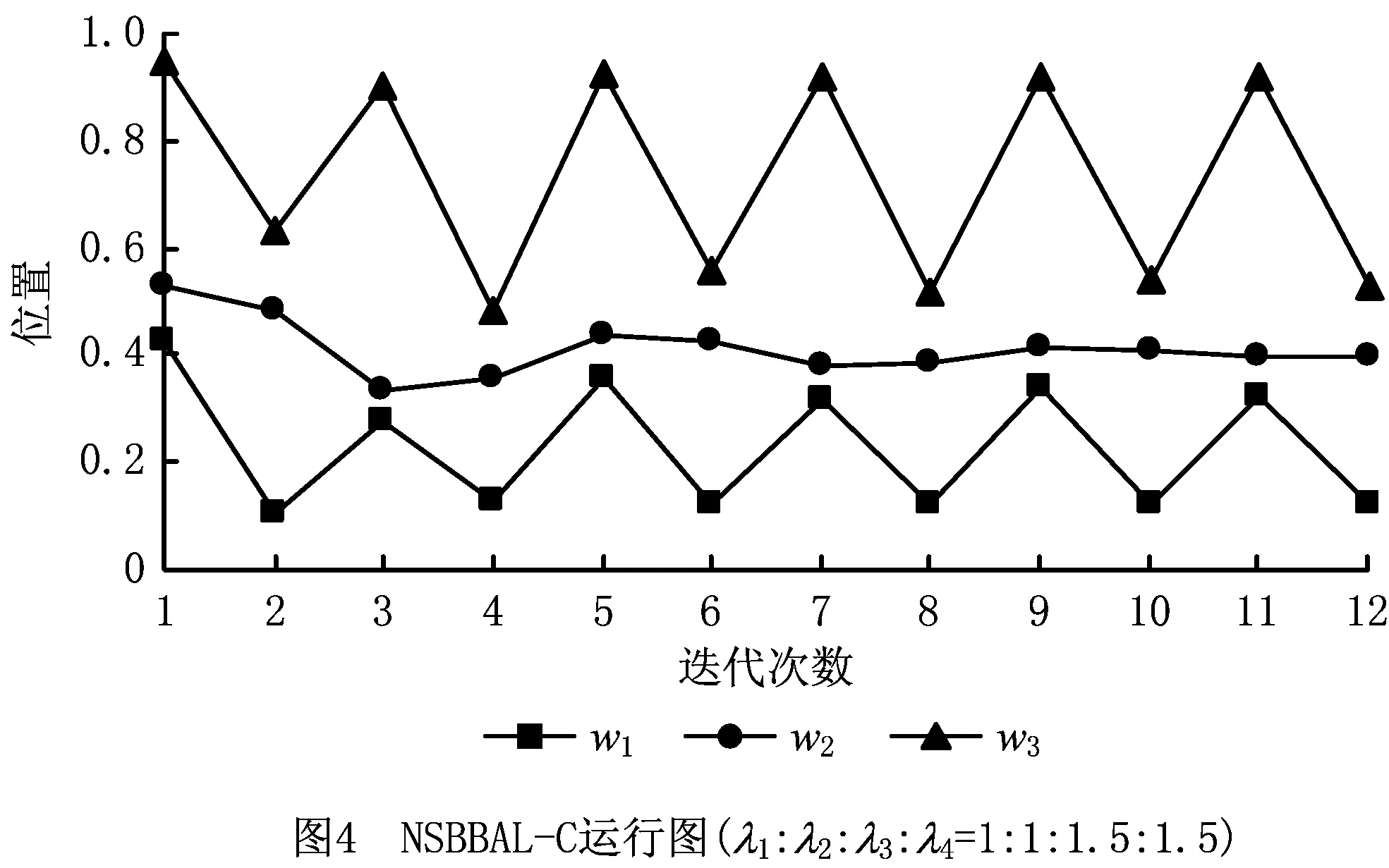
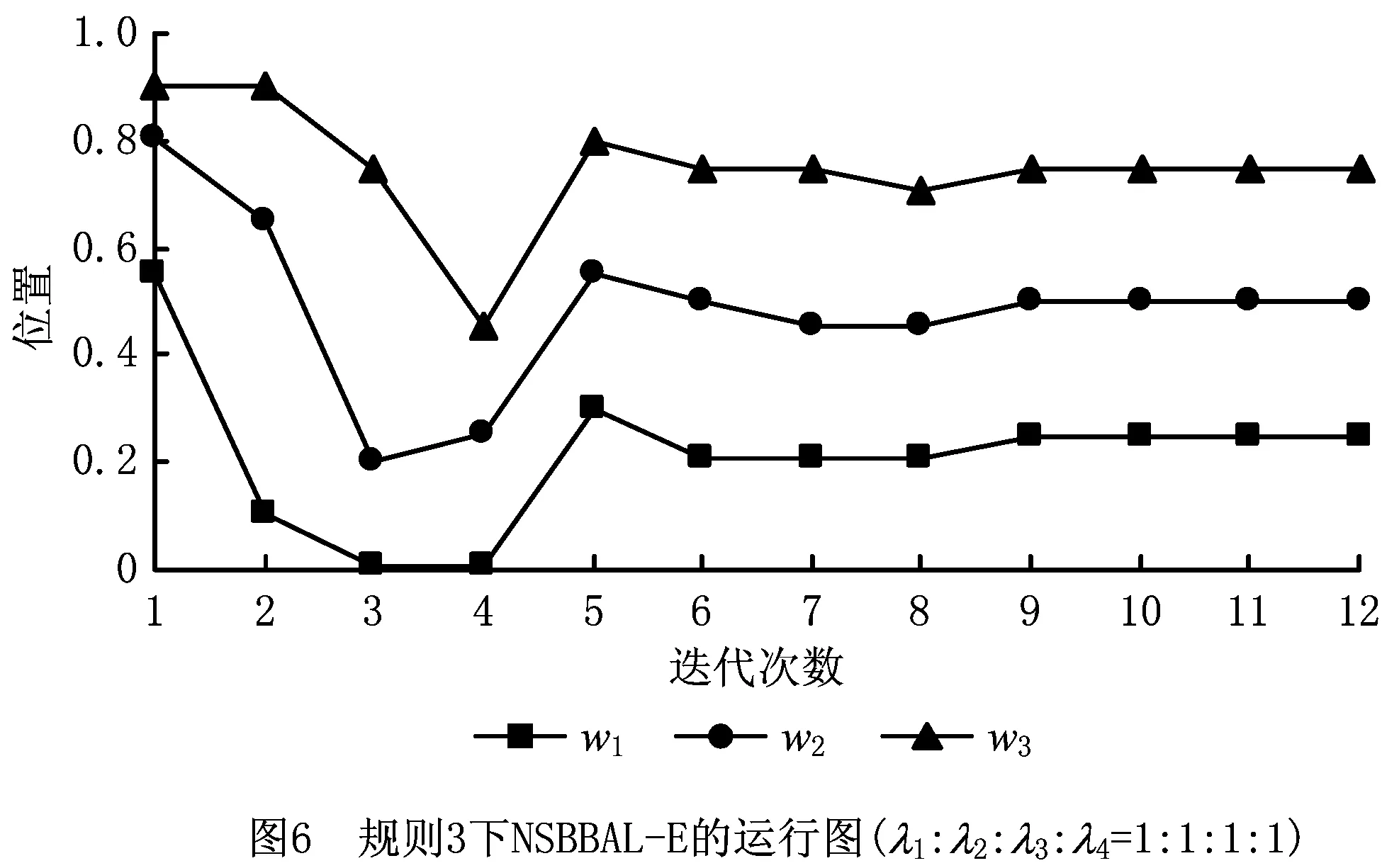
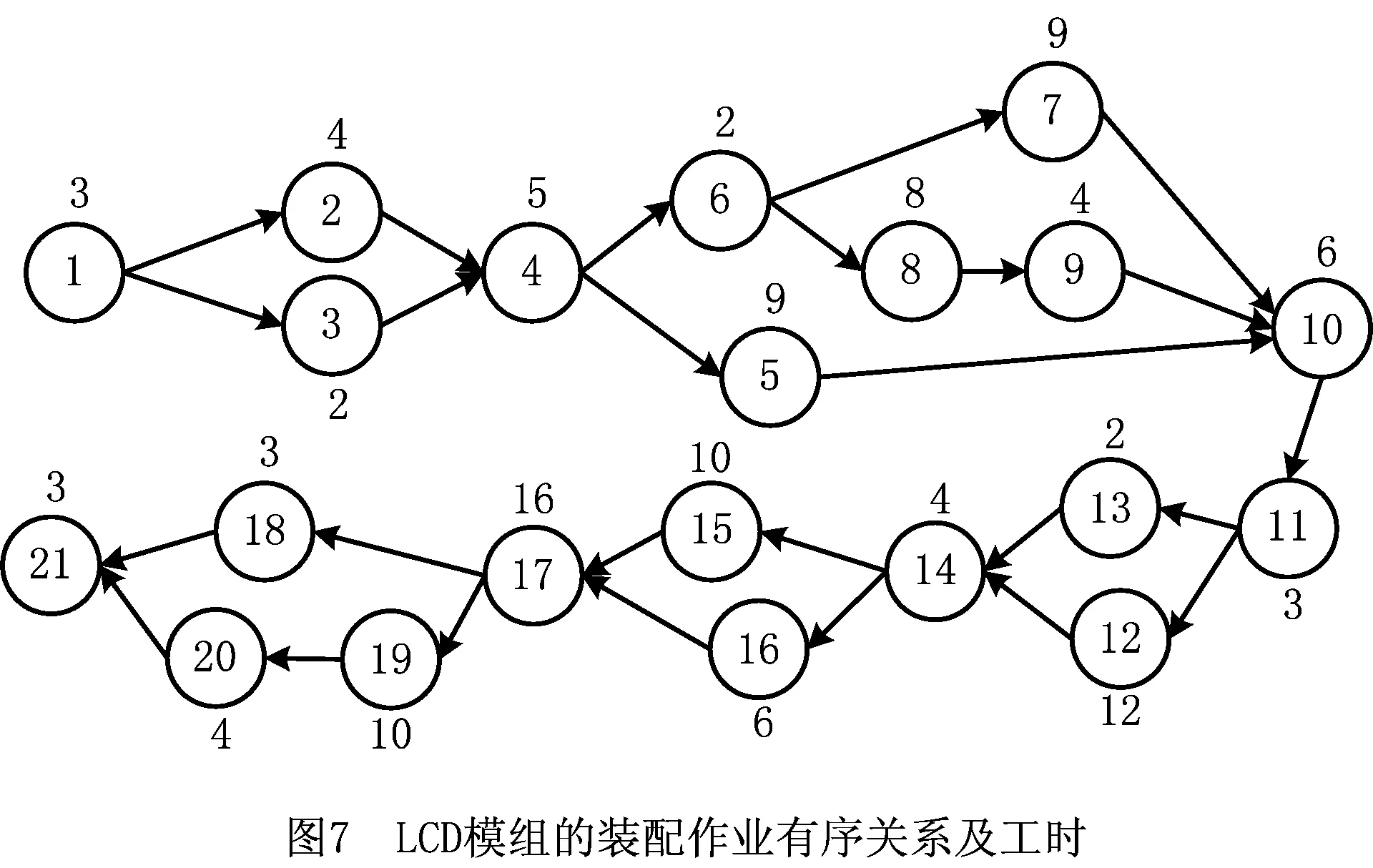
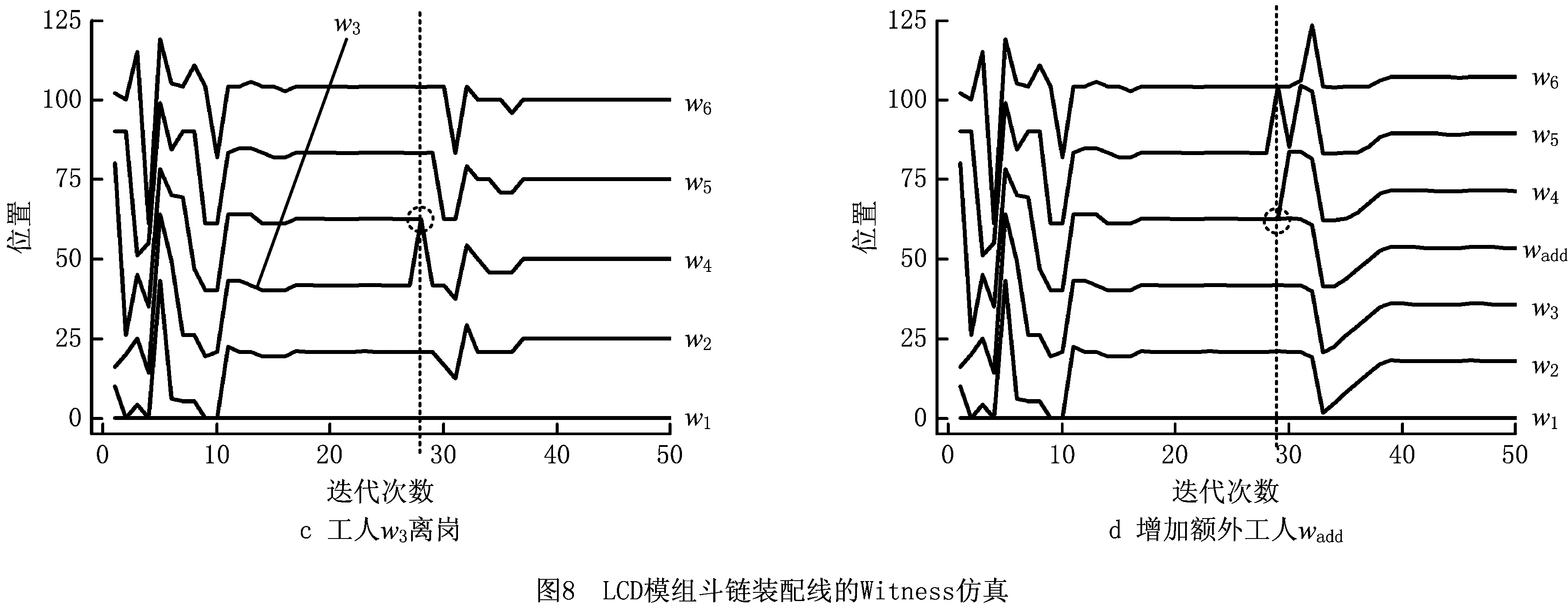
在约束②和约束③下,所有工人在同一时刻完成任务交接,若定义装配线长度为单位长度1(无量纲),可用工人位置xj(0≤x1<… 定理1对于自平衡的生产线,均存在一个平衡点X*=f(X*),即存在位置状态向量X*,如果每名工人从X*给定的对应位置开始作业,则其总是在该位置接手下一个任务。 定理2若工人按作业速度沿生产线严格递增排列(作业速度越低的工人在排列中越靠近生产线始端),则平衡点是唯一的,该平衡点 (1) 上述定理描述了斗链的自平衡性,即存在一个平衡点X*,工人从任意状态X0给出的位置开始工作,最终均能收敛至平衡点X*。在文献[17]中,NBBAL已被证明具有自平衡性,其证明过程如下: (2) (3) 根据式(3),NBBAL的状态转移过程是一个Markov链,可表示为 Xr=T×Xr-1+λ。 (4) Xn=(0,v1tn,v1tn-1+v2tn,v1tn-2+v2tn-1 +v3tn,…,v1t2+v2t3+…+vn-1tn)T。 (5) 若记v1/vn=a0,(vj-vj-1)/vn=aj-1(j=1,2,…,n-1),则 (6) 在迭代次数r≥n时, (7) 因为λ1<λ2<…<λn,即v1 ∑aj=1,0 (8) 在NSBBAL中,式(4)所示的Markov链模型仍然成立,即方程X=T×X+λ存在唯一解X*=(E-T)-1×λ,系统具有唯一的平衡点。首先分析“<”个数为0,即NSBBAL-E(λ1=λ2=…=λn)的情况,此时式(7)中系数a0=1,a1=a2=…=an-1=0,可得 (9) (10) (11) ∀j∈[1,n]。 (12) 式(12)表明状态向量Xn=X0,即经过n次迭代后,系统回到初始状态,系统的可达状态是一个有限集合{X0(Xn),X1,…,Xn-1},系统在可达状态集内循环迭代(X0→X1→…→X0→X1→…),即NSBBAL-E不具有从任意状态收敛的能力。即使令X0=X*,系统也仅是理论上处于平衡状态(X*→X*→…),由于实际生产环境存在干扰,系统从平衡位置偏离后,不能重新收敛到平衡。 在更一般的情况下,不妨设λ1≤λ2≤…≤λn中存在q(0 (13) 记d1,d2-d1,d3-d2,…,n-dq的最大公约数为d(工人按作业速度分组,d为每组人数的最大公约数),另记d1/d=p1,d2/d=p2,…,dq/d=pq,则在迭代次数r≥n时式(7)表示为 … … 因为式(13)中非零系数之间的最小间隔为d,所以上述迭代过程存在d个相互独立的递推数列 … … … d1,d2-d1,d3-d2,…,n-dq的最大公约数为d,也就是按照排列每d个工人速度相等,即λn-(d-1)=λn-(d-2)=…=λn-1=λn,则 (14) 式(14)说明,随着d个独立递推数列的分别收敛,工人wn-(d-1)的任务交接位置收敛至同一点,同理可以证明工人wd+1,w2d+1,…,wn-(d-1)的任务交接位置收敛。若n/d=nd,则按作业速度可将工人分为nd个工人组{dwk|k=1,2,…,nd},即dw1={w1,w2,…,wd},dw2={wd+1,wd+2,…,w2d},…。若将dwk作为一个整体,则所有dwk的任务交接位置均收敛,符合定理1和定理2所述的自平衡性。NSBBAL-C存在以下定理: 定理3在NSBBAL-C中,若以nd个工人组dwk作为个体,且工人组作业速度递增(非严格)排列,则以dwk为个体装配线可以从任意状态收敛至唯一的平衡点,该平衡点 (15) 由定理3可知,若最大公约数d=1,则n=nd,dwk=wk(j=1,2,…,n),此时NSBBAL-C具有从任意状态收敛的自平衡特性。 本文基于C++Builder 2010进行数值建模与仿真。由于任务交接在xn=1时刻同时进行且瞬时完成,则任务交接位置状态与xn=1时状态一致,以xn=1时的状态X为观察对象,记录迭代过程中w1~wn-1的位置变化。 图2所示为文献[17]对NBBAL的数值仿真结果,从图2数据可看出,NBBAL收敛于唯一的平衡点,平衡点特性符合定理1和定理2。 从图3仿真结果可以看出,在规则1和规则2下,NSBBAL-E不具有从任意状态收敛的能力,系统在可达状态集内循环迭代,仿真结果与前面推导结论相符。 从图4仿真结果可以看出,按作业速度对工人以d分组,以dwk为工人个体,则dwk任务交接位置向平衡点收敛,仿真结果与定理3相符,即从w1开始每隔d个工人存在一个收敛的任务交接位置。 图5所示为最大公约数d=1时的NSBBAL-C仿真结果,此时wk=dwk,NSBBAL-C具有定理1和定理2所述的自平衡性。与图2相比,其收敛速度小于NBBAL。 (16) 在工人沿装配线按作业速度严格递增排列时,λ1<λ2,则可得 (17) 由式(17)可看出,严格递增作业速度(λ1<λ2)的NBBAL中存在一个负反馈控制,在交接位置偏离平衡点时,使偏离差值Δx2向零收敛。速度比(λ2/λ1)越大,负反馈控制作用效果越强,这也解释了图5收敛速度比图2慢的原因。 在实际生产中,考虑同质员工的NSBBAL-E具有更现实的意义。由定理3及式(17)可知,当作业速度系数为λ1<λ2=…=λn(d=1)时,负反馈的控制作用仍然存在。因此,在规则1和规则2的基础上为NSBBAL-E增加如下规则: 规则3对于首名工人w1,若其与w2的距离x2-x1小于1/n,则w1停止作业;若距离大于1/n,则按规则1进行;当任务被接手后,按规则2返回。 规则3限制w1与下游工人的距离,令Δx2强制置零,继而实现下游各Δxj的归零,使系统最终收敛于平衡状态,其作用效果如图6数值仿真结果所示。 从图6可以看出,规则3使NSBBAL-E从任意状态向平衡点收敛。与NBBAL的基本规则相比,规则3仅增加了对w1与下游工人距离的限制,且对于装配线始端的首名工人w1来说,这种距离的限制在实际生产中是容易实现的。 综上所述,NBBAL,NSBBAL-C和NSBBAL-E的自平衡特性如表2所示。 某电子产品由主板模组、上盖模组、液晶显示屏(Liquid Crystal Display, LCD)模组和其他关键零部件组合而成,其中LCD装配线的作业有序关系及标准作业时间如图7所示。该产品生产线全部采用固定工位组织形式,其生产效率及稳定性受市场波动及人员流动的影响较大,因此现在需要基于NSBBAL-E模型对LCD装配线进行斗链生产的示范性规划。目前,LCD装配线由6个工位S={s1,s2,…,s6}组成,作业分配情况及工位作业时间st为:s1(1,2,3,4,5),st1=23;s2(6,7,8,9),st2=23;s3(10,11,12),st3=21;s4(13,14,15,16),st4=22;s5(17,18),st5=19;s6(19,20,21),st6=17。其生产节拍C=max(st)=23。 基于实际生产数据,建立LCD斗链装配线的Witness模型,如图8a所示。根据标准作业工时,将装配线长度定义为125(st1+st2+st3+st4+st5+st6),并采用6名同质员工作业,以满足原生产节拍要求。LCD斗链装配线的正常运行如图8b所示,其具有从任意状态收敛的自平衡性,此时生产节拍C=125/6≈21,生产效率显著提高;在需要调整生产效率,或由于发生动态干扰,工人数量变化时,它也可以通过自平衡性重新收敛至平衡状态,以保证最大人均效率,如图8c和图8d所示。 本文在NBBAL的基础上,对NSBBAL进行了建模及数值仿真研究,分析了其平衡点特性和向平衡状态收敛的能力,并提出NSBBAL-C的平衡点存在定理,继而给出NSBBAL-E的运行规则,实现了其有效运行,为斗链在实际装配生产中的应用提供了一定的理论基础和研究思路。 本文对BBAL的模型分析和Witness仿真,是基于约束③“作业均匀连续分布,交接可在任意位置进行”,但在实际生产中,有些工序是不宜中断的,如图7中的作业16(撕除导电布背胶,贴于螺丝孔上)。此时若中断作业进行任务交接,则会增加工时;若让下游工人等待,则影响生产效率。因此,BBAL虽然不存在平衡问题,但仍需考虑作业分配顺序问题,以保证交接耗时最小,这将是下一步的研究内容。



3 NSBBAL自平衡性的建模分析及数值仿真
3.1 NSBBAL-E模型
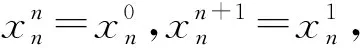
3.2 NSBBAL-C模型

3.3 数值仿真


4 NSBBAL-E的自平衡方法
4.1 自平衡中的负反馈控制
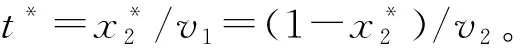

4.2 NSBBAL-E的新规则

5 生产实例的Witness仿真

6 结束语
