变“适应”为“促进”，实现学生个性化发展——《长方形和正方形的面积》教学实践与思考

江苏南通市天生港小学 缪 谦

数学课程标准指出：“教学中应尊重每个学生的个性特征，允许不同的学生从不同的角度认识问题，采用不同的方式表达自己的想法，用不同的知识与方法解决问题。鼓励解决问题策略的多样化，是因材施教、促进每个学生充分发展的有效途径。”这一表述强调了数学教育“个性化”的价值取向。笔者曾执教了《长方形和正方形的面积》一课，磨课的过程让笔者对如何促进学生“个性化发展”有了新认识。

一、设定差异目标，由负担变为资源

教学应立足于学生数学能力的差异，教师不应将差异看成负担，而应看作资源，并通过教学活动设计、师生互动交往等手段充分开发和利用这一资源。

《长方形和正方形的面积》一课在图形面积计算教学中占据着“认知原点”的地位。这是学生在建立了面积概念后，对平面图形面积计算公式的起始性探究。而在这次探究过程中所获得的对公式意义的理解将成为学生将来探索其他平面图形面积计算方法的“地基”。为了帮助学生夯实“地基”，让其获得原始的意义支撑，笔者在探究长方形面积计算公式的首个环节设计了让学生用面积单位来“摆量”长方形面积的操作活动。

教学片段：

出示长4分米，宽3分米的长方形。

师：想知道这个长方形的面积有多大吗？用哪个单位来计量它的面积比较合适？

生：平方分米。

师：（出示1平方分米）能估计一下，这个长方形的面积大约是几平方分米吗？

生1：一行大约摆4个，大约能摆3行，所以是12平方分米。

生2：一行大约摆3个，大约能摆2行，所以面积约是6平方分米。

师：怎么才能知道它的面积到底是多少？

生：可以用面积是1平方分米的正方形来摆。看一共能摆几个1平方分米的正方形，长方形的面积就是几平方分米。

师：他的意思其实就是要知道——一共能摆几个面积单位？解决了这个问题，就知道了这个长方形的面积。

师：下面老师就想让大家用摆的办法来找到这个图形的面积……

设计的意图是让数学能力存在差异的学生用不同的方法解决问题，产生多样化的摆量方法。

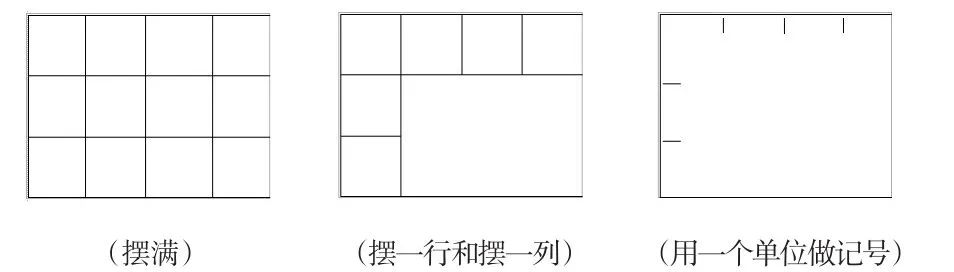
通过对不同“摆量”方法的共性比较形成本质性的认识，建立起长方形面积计算公式和其原始意义的对应关系。利用这些逐步简化的“摆量”方法来实现学生的认识从具体到抽象的深化，促进不同数学能力的学生都得到充分的发展。

二、给予差异条件，由矛盾引发探究

因为学生个体内在的数学能力存在差异，所以教师提供的外部学习条件也要存在相应的差异。三年级学生以具体形象思维为主，如果提供给学生的面积单位都足够摆满长方形，他们在解决问题时将一致选择最符合自己认知特点的方法——摆满。这样就无法出现预期的方法多样化，学生表现出来的思维水平将没有差异，而且维持在一个较低层次的水平上。为了让学习能力不同的学生得到不同的外部学习条件，笔者课前将学生进行了学习能力的同质分组，将学生分成学习能力较弱、中等和较强的三类，同时为这三类小组分别提供了不同的面积单位的个数。

第一次试教片段：

师：下面就来动手摆一摆，看看这个长方形的面积到底是多少？

生：没有1平方分米的正方形怎么摆呀？

师：老师给你们准备了。第一组和第二组（能力弱），根据刚才的估计，老师各发给你们15个。第三组和第四组（能力中等），老师只为你们准备了8个，在解决问题的过程中，要多动脑筋。剩下的两组（能力强）老师只为你们准备了一个，能不能解决问题就看你们的本领了。（学生议论纷纷）

生：1个太少了。

师：老师也觉得和其他组相比，1个的确少了些，不过这正是个挑战，老师相信你们通过思考，能解决这个难题。

从汇报结果看，能力弱的2个小组都运用“摆满”的方法；能力中等的4个小组都运用了“摆一行和一列”的方法；能力强的2个小组都运用了“用一个面积单位做记号”的方法。课前预想的三种摆量方法如约而至。

反思教学过程，笔者在课前将学生分组，是把握了学生的个性特点、学习情况和学习能力等方面的差异。为学习能力不同的小组提供了不同的外部学习条件，做到了从学生的实际出发，能针对不同学生的不同情况实施差异教学。从整体来看，就是以学习者的主体性为导向，提高了教学预设的针对性。而提供的面积单位不足以摆满长方形，这就与学生的思维特点产生了矛盾。这个矛盾恰恰能促使他们寻找到更简洁、更抽象的方法。由此，不难看出教学时为学生提供的学习外部条件应该足以与学生个体的内在数学能力之间发生矛盾，这样才能实现“不同的人在数学上得到不同的发展”。

三、设置差异变量，由预设变为生成

差异教学就是要以生成为导向，提高预设的针对性、开放性和可变性，追求教学内容、方式方法在共性基础上的多样性、灵活性，给学生提供选择的机会，使“外因”和“内因”的矛盾维持一定的张力，从而实现不同能力的学生能有共同而有差异的发展。如果以学生的个性化发展为导向，原来的教学预设的开放性和可变性还有待提高。

第二次试教片段：

师：下面我们就动手摆一摆，看看这个长方形的面积到底是多少？

师：老师准备了一些1平方分米的小正方形，放在这些信封里。不过，这里面的小正方形个数有多有少，有的里面装了15个，有的里面装了8个，还有里面只有1个。（学生有些疑惑）

师：是不是每个信封都能解决问题？如果老师让你来抽一个信封，你希望抽个数多的，还是抽个数少的？

学生分组议论

师：下面就请每个小组派一个代表来抽取你们需要的信封。（学生自主抽取信封）

师：现在每组同学都抽到了自己需要的信封。不过不管你是抽到多的，还是抽到少的，抽到的正方形需要几个就用几个。

这次教学笔者放弃了将学生按照数学学习能力的强、中、弱同质分组的方式，改为自然异质分组，以提高学生分组的随机性。这些随机形成的学习小组又通过抽签的方式来获得不同个数的面积单位，学习个体就增加了外部学习条件获得的自主性。

接着教师提出了两个问题：“是不是每个信封都能解决问题？”“如果老师让你来抽一个信封，你希望抽到个数多的，还是抽到个数少的？”和一个提示：“不过不管你是抽到多的，还是抽到少的，抽到的正方形需要几个就用几个。”让学生来实现个体获得外部学习条件的动态性。

在这样的引导下，学生汇报的结果是：共两组抽到了15个面积单位，其中一组选择“摆满”的方法，另一组选择“用一个面积单位做记号”的方法；共四组抽到了8个面积单位，三组选择“摆一行和一列”的方法，一组选择“用一个面积单位做记号”的方法；共两组抽到1个面积单位，都成功地运用“用一个面积单位做记号”的方法。

这次教学与原先相比，学习过程让学生有了想的空间和做的余地。教师在教学过程中注意了面向全体学生，使不同能力的学生得到了与其数学能力相适应的个性化发展。

教学实践告诉我们：过往的教学中，我们在面对学生的个体差异时总是选择消极的“适应”。教学的积习，让我们把正态分布中中间水平的学生作为主要的教学对象。也就是学生个体数学能力的“平均数”。但我们知道，“平均数”只是一个虚拟的数。数学教学只有在高度地尊重真实存在的学生个体差异和细心地研究学生个体差异的基础上，变被动的“适应”为主动的“促进”，才能实现每个学生的个性化发展。♪