压−弯−扭共同作用下闭口截面钢构件弯矩作用平面内极限承载力
2018-09-07韩庆华程禹皓芦燕
韩庆华,程禹皓,芦燕
压−弯−扭共同作用下闭口截面钢构件弯矩作用平面内极限承载力
韩庆华1, 2,程禹皓1,芦燕1, 2
(1. 天津大学 建筑工程学院,天津,300072;2. 天津大学 滨海土木工程结构与安全教育部重点实验室,天津,300072)
利用Umansky闭口截面扭转理论,在现行GB 50017—2003“建筑钢结构规范”的基础上,得到适用于压−弯−扭共同作用下闭口截面构件弯矩作用平面内极限承载力的计算方法;采用数值分析方法对提出的设计公式进行验证,在建模时引入初始几何缺陷和残余应力,在分析时考虑几何非线性和物理非线性的影响;最后针对扭矩作用下矩形截面压弯构件截面塑性发展规律进行分析。研究结果表明:本文所提出计算公式能够真实反映构件的受力状态,使用便捷;在压力、弯矩和扭矩共同作用时可能存在的7种荷载路径对矩形截面钢管的极限承载力几乎没有影响;构件的抗弯和抗压极限承载力随着扭矩的增大而降低,且降低的程度越来越大;约束扭转的存在只会使截面最危险点更早地进入塑性状态,而对截面最终承载能力的影响不大,因此,根据自由扭转理论提出的设计公式对于存在约束扭转的矩形截面构件依然适用。
压−弯−扭共同作用;闭口截面;弯矩作用平面内极限承载力;约束扭转;荷载路径
闭口截面的钢管作为一种常见的构件,具有较高的抗弯和抗扭抵抗力,且能够较好地满足建筑美观需要,因此被广泛应用于框架柱、桥梁的箱梁、空间结构杆件以及交通指示牌立柱等需要承受复杂荷载情况的建筑物或构筑物。对于诸如风荷载作用下的悬臂交通指示牌立柱等构件会同时受到压力、弯矩和扭矩的作用,因此,有必要对压−弯−扭共同作用下闭口截面钢管的极限承载力进行分析。目前,人们对于压弯构件承载力已进行深入研究,各国规范中也有着明确的规定[1]。对于在弯扭共同作用下构件承载力的相关问题,人们也进行了大量研究。KIM等[2]对弯扭构件极限承载力预测公式进行了简化,提出了适用于设计的承载力下限,在建模时考虑了残余应力与几何初缺陷的影响,并且在分析时考虑了几何非线性和材料非线性;陈宜言等[3]对弯扭共同作用下圆形截面钢管进行了有限元分析,但其分析时没有考虑初始缺陷的影响。总体而言,人们对于压弯构件极限承载力的研究主要集中在其整体稳定问题,而对于弯扭构件极限承载力的研究主要集中在板件局部稳定问题。现行的 GB 50017—2003“钢结构设计规范”[4]中仅给出了压弯作用下构件的平面内和平面外稳定设计方法, GB 50018—2002“冷弯薄壁钢结构技术规范”[5]中给出了考虑约束扭转对截面翘曲影响后的弯扭构件平面外稳定(弯扭失稳)设计方法。而在美国钢结构协会(AISC)最新的设计规程[6]中所提出的压−弯−扭共同作用下钢管极限承载力设计公式,依然采用的是FELTON等在试验研究基础上针对方钢管和圆钢管提出的理论,由于试件涵盖的构件种类比较少,因此,参考价值一般。人们对扭矩对压弯构件弯扭失稳的影响进行了研究,并得到了相应的设计方法[7]。而我国目前针对钢构件在压−弯−扭共同作用下的研究较少。罗尧治等[8]对双锥型压−弯−扭圆钢管进行了试验研究,并采用有限元法对试验进行了模拟,分析中考虑到几何非线性和材料非线性,未考虑初缺陷的影响。曹哲玮[9]对压−弯−扭共同作用下的冷弯矩形钢管进行了试验研究并基于试验结果总结了设计公式。田兴 运[10]对扭矩对弯扭共同作用下的弯扭失稳的影响进行了解析分析并得到了建议设计公式。压−弯−扭共同作用下的构件除了在弯扭作用平面外产生稳定问题(弯扭失稳)外,当构件平面外的变形受到足够约束或构件截面受扭不产生翘曲时,构件将在弯矩作用平面内失稳。而现在对于压−弯−扭构件弯矩作用平面内的研究主要集中于钢管混凝土构件[11−13],对于钢构件反而缺乏相关研究,因此,有必要对压−弯−扭共同作用下钢构件弯矩作用平面内的极限承载力进行研究。荷载种类的增多产生了多种荷载路径,即荷载的加载顺序有着多种形式。陈宜言等[3, 14]对压弯构件和弯扭构件进行了研究,认为荷载路径对构件极限承载力的影响很小。但对于压−弯−扭共同作用下的构件,荷载路径种类更多,因此,需要进一步进行研究。本文作者针对压−弯−扭共同作用下闭口截面钢构件在弯矩作用平面内的极限承载力进行研究。在GB50017—2003“钢结构设计规范”[4]给出的压弯构件平面内稳定极限承载力公式的基础上,考虑自由扭转理论中的相关假设,得到压−弯−扭共同作用下构件弯矩作用平面内极限承载力设计公式;利用试验验证后的有限元模型对该公式进行验证,证明其适用于工程中常见的圆钢管和矩形截面钢管等构件;利用有限元方法对荷载路径对极限承载力的影响进行研究。
1 压−弯−扭共同作用下闭口截面钢构件平面内极限承载力计算公式推导
压−弯构件极限承载力的求解通过GB50017—2003“钢结构设计规范”[4]中平面内稳定计算公式进行。

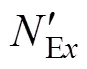
该公式以轴心受压构件考虑初缺陷和塑性变形得到弯曲屈曲临界力为基础,以弯矩最大截面的边缘纤维开始屈服并考虑进一步的截面塑性发展为准则推导得出。是一个半理论半经验的设计方法。
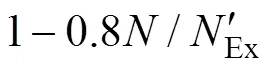
对于一般的压弯构件,在构件的最危险截面上,最大正应力一般在弯矩平面内的受压边缘处,而剪应力最大值一般出现在弯矩作用平面内的中性轴处,而在最大正应力的位置,剪应力一般为0 MPa。故在压弯构件中以max=[]作为判断边缘纤维屈服的准则是合理的。
但对于承受扭矩的构件,以单室闭口截面为例,根据自由扭转理论,截面上产生的剪力流均匀分布,此时最大正应力位置处剪应力也最大,继续使用max=[]作为边缘屈服的准则而不考虑剪应力对屈服的影响可能会引起较大误差。因此,得到压−弯−扭共同作用下构件平面内极限承载力计算公式的关键是将复杂应力情况下构件的屈服准则和塑性发展形式引入到构件屈服判别准则中。
轴心受压构件在弹性阶段的弯曲屈曲欧拉力计算公式如下:
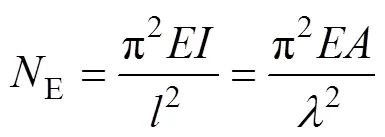
式中:E为构件欧拉力;为构件的计算长度;为弯矩作用方向构件长细比。欧拉力公式在临界应力cr<y时构件处于弹性状态发生屈曲,有较高的准确性。但当cr>y时,构件将在弹塑性状态发生屈曲,这时欧拉公式将不再适用。
考虑截面的塑性发展可以得到在材料发生弹塑性屈曲时的临界荷载cr:

式中:e为考虑塑性发展后的截面惯性矩。在此基础之上进一步考虑残余应力对构件弹塑性性能的影响。通过大量试验和数值分析,最终可以得到柱子曲线和稳定系数。轴心受压构件的稳定性计算公式为
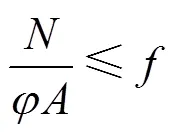
图1所示为压−弯−扭共同作用下的悬臂构件(其中,和分别为构件受到的轴力和扭矩,为推力)。以图1中悬臂构件为例,在考虑轴心受压构件弯曲屈曲临界力的基础上对压−弯−扭共同作用下构件的极限承载力计算公式进行推导。

图1 压−弯−扭共同作用下的悬臂构件
假定构件只发生自由扭转,即在构件变形过程中构件的扭转角和弯曲转角不耦合[15],可以认为扭矩与轴向压力和弯矩均不发生二次作用。
在弯矩作用下在自由端产生的挠度为m。当作用于轴心力后,根据式(2)可得在弹性范围内自由端挠度增加为

式中:=/E,为量纲一轴向力。
在推力引起的端弯矩和轴向压力作用下的固定端极限弯矩max为



进一步考虑各种初缺陷并将其等效为与原变形情况相似的初始挠度0。计算弯矩取为端弯矩,则固定端总弯矩为

对于复杂应力作用下,材料由弹性状态转入塑性状态的情况能够很好地用von Mises准则体现。针对本文钢构件所受的压弯正应力和扭转剪应力,等效应力eq可以简化为

式中:y为钢材屈曲强度。
在此基础上,考虑构件固定端处截面外边缘纤维达到屈曲时,构件外荷载应满足:

式中:为抗弯惯性矩;p为抗扭惯性矩。
对于压弯构件的塑性发展,由于轴向压力引起的材料非线性已经通过稳定系数考虑,故应单独考虑弯矩作用对塑性发展的影响,对截面抗弯抵抗矩进行放大。图2所示为矩形截面钢构件截面塑性发展形式。在考虑压、弯、扭三者共同影响时,由于假定闭口截面构件只发生自由扭转,轴向压力和扭矩引起的应力在截面上均匀分布,不会改变塑性发展的形式和程度(塑性发展的形式见图2(a),其中箭头方向表示塑性发展方向),故为便于公式推导,将塑性发展等效为屈服强度的提高即γfy,最终得到极限状态下内力和应力的关系(见式(9))。此时,γ将同时对轴力和弯矩项进行放大,轴向压力作用下材料的非线性通过和γ考虑了2次,此处的重复考虑可以在式(12)代回求解极限承载力时也将γ假设为轴力和弯矩共同作用下的塑性发展系数来进行修正[16]。悬臂构件自由端横向力作用下产生的弯曲剪应力比弯曲正应力小得多(对于本文算例小于5%),故采用与现行规范[4]中相同的简化方式(式(9)中未考虑弯曲剪应力的影响)。

令=0,=0,则有初始缺陷的轴心受压构件弹塑性稳定表达式为

将轴心受压稳定承载力0=y代入式(11)可得

将式(12)代入式(10)可得

令等效轴向压力系数为n,则有

最终得到压−弯−扭共同作用下构件的平面内极限承载力计算公式:

采用与压弯构件平面内稳定设计方法中相同的安全冗余考虑方法,取折减后的E(E=π2/(1.1λ2))代替E[4],代替y,最终得到设计公式如下:

式(15)和(16)是基于假设构件在扭矩作用下只发生自由扭转的假定得到的。根据Umansky闭口截面薄壁杆件约束扭转理论,对于闭口截面薄壁直杆,在扭矩作用下构件的扭转变形平衡微分方程为


2 有限元分析
2.1 分析模型
参考文献[9]中对压−弯−扭共同作用下的悬臂冷弯矩形钢管的试验分析,验证本文的有限元分析方法。分析模型简图如图3所示,截面长×宽×壁厚分别为250 mm×250 mm×6 mm(模型A),300 mm×200 mm×6 mm(模型B),350 mm×150 mm×6 mm(模型C),钢材采用A36钢。加载制度参照试验,先将轴向压力加载到0.1y(y为全截面塑性轴心受压抵抗力),然后逐渐施加偏心横向力直至构件破坏。对于3种截面的模型采用大偏心横向力(偏心距为920 mm)和小偏心横向力(偏心距为460 mm)分别进行加载(横向力方向垂直于模型长边方向),最终得到6个模型的数值模拟结果。

数据单位:mm
采用C3D8R实体单元建立有限元模型(FEM),C3D8R是一种较为通用的单元类型,既能够广泛地适用于各种线性和非线性分析,又具有适中的精度[17]。试件有限元模型如图4所示。考虑到支撑刚度和冷弯过程对冷弯矩形钢管转角部位钢材本构的影响,将构件按材料性质分为3个部分。试件平板部位采用理想弹塑性模型。试件转角部位的钢材由于受到辊弯 作用的影响而不再具有明显的屈服平台,因此采用Ramberg-Osgood模型表示。本构模型如图5所示。

式中:为材料应变;为本构曲线转弯处的弯曲程度;Yc为名义屈服应力,通常取塑性变形为0.2%时对应的应力。Ramberg-Osgood公式通常通过大量试验结果拟合得到。KEY等[18]针对A36冷弯方钢管的研究表明,取15时能够很好地模拟转角处真实的材料本构;由于上盖板连接有大刚度加载构件,加持段试件填充有混凝土,故将二者刚度设置为试件部位刚度的100倍,以便近似模拟刚性构件。由于试验并未提供材性试验结果,故本文选取A36钢材料性质的通常取值来赋予材性,弹性模量=206 GPa;直板部位名义屈服应力Yf=250 MPa;转角部位名义屈服应力Yc=250 MPa;泊松比= 0.3。
1—试件平板部位;2—试件角部;3—上盖板和加持段。
图4 有限元模型
Fig. 4 Finite element model

图5 本构模型

图6 残余应力分布形式
计算非线性极限承载力时考虑试件的几何初始缺陷和冷弯过程中产生的残余应力对于提高分析精度是十分必要的。几何初始缺陷的最大幅值通过参考GB 50017—2003“钢结构设计规范”[4]中关于构件加工精度的要求,定为试件总长度的1/1 000[19]。而其几何初缺陷的变形形式则通过特征值屈曲分析选取与试验中构件破坏形式相符的第一阶屈曲模态来进行。而对于冷弯矩形钢管的残余应力,由于同时受热轧和冷弯过程的影响,残余应力的分布形式复杂,因此本文主要基于KEY等[18]针对冷弯方钢管进行试验研究后得出的模型进行分析。以A截面试件为例,将残余应力代入ABAQUS有限元模型之后的应力云图如图6所示(其中最小应力位于钢管外侧,为负(压应力);最大应力位于钢管内侧,为正(拉应力))。
2.2 有限元分析结果与试验结果对比
表1所示为构件极限承载力有限元分析结果与试验结果对比。从表1可以看出:除小偏心构件受扭的截面B模型外,极限承载力的误差均在10%以内,说明有限元分析模型具有较高的精度。
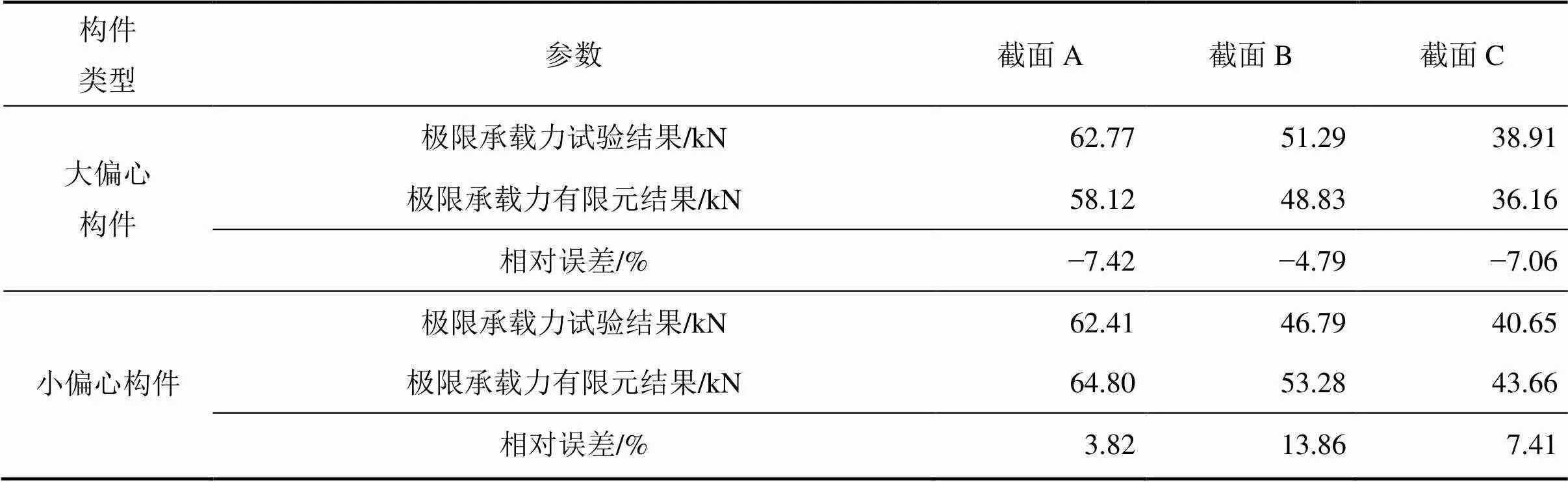
表1 极限承载力有限元分析结果与试验结果对比
3 荷载路径对极限承载力的影响
在实际工程中,受到多种荷载作用的构件有着多种受力状态。在不同受力状态下可能存在着不同极限状态。对于在压−弯−扭共同作用下的构件,可能的7种荷载路径如图7所示。
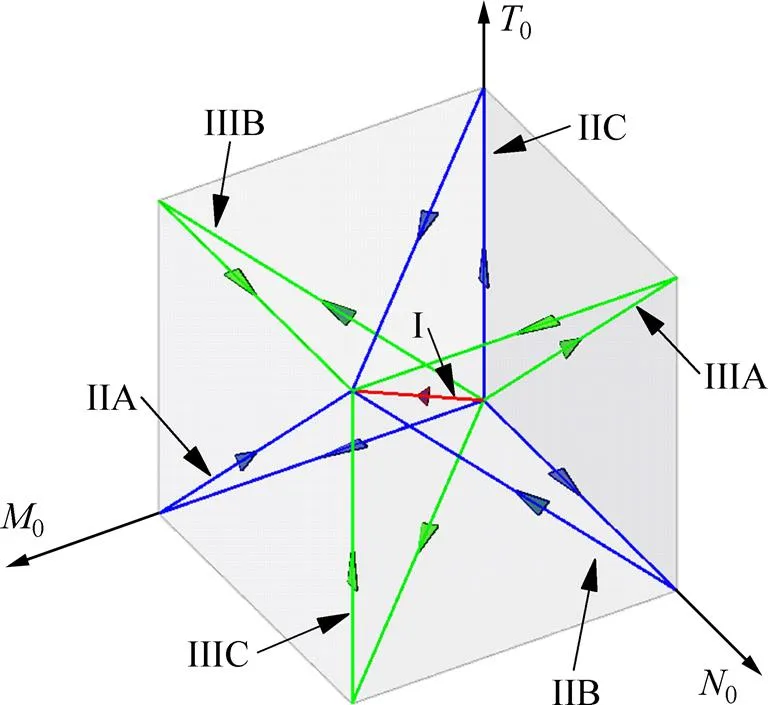
图7 压−弯−扭共同作用下试件荷载路径
分析时,弯矩、轴向压力、扭矩按照一定比例(::=p:p:p,其中p,p和p分别为全截面塑性时的弯矩、轴向压力、扭矩承载力)加载直至构件破坏,得到极限承载力u0,u0和u0。图7中坐标轴代表的量纲一弯矩0、轴向压力0、扭矩0为各种荷载路径极限状态下的各种荷载分别与u0,u0和u0的比值。路径I即为由原点到(1,1,1)的向量,表示3种荷载按全截面塑性抵抗力的比例逐渐增大直至达到极限状态。
路径II存在3种情况。分别令弯矩、轴力和扭矩保持为u0,u0和u0不变,另外2种荷载按照全截面塑性抵抗力的比例逐渐增大,直至构件达到极限承载力,最终可以得到路径IIA,IIB和IIC。
路径III也存在3种情况。分别令轴力和扭矩保持为u0和u0,弯矩和扭矩保持为u0和u0,或弯矩和轴力保持为u0和u0,使另外1种荷载逐渐增大,直至构件达到极限承载力,最终可以得到路径IIIA,IIIB和IIIC。
以截面长×宽×壁厚为250 mm×250 mm× 6 mm的模型为例进行研究,将各种路径得到的量纲一极限承载力作为坐标绘制在三维直角坐标系中,不同荷载路径下极限承载力对比如图8所示。通过坐标点的位置以及坐标点与3个坐标平面围成的立方体可以看出7种荷载路径的极限承载力几乎相等。
为了能定量地对荷载极限承载力进行对比,将增量分析时表示荷载增长程度的荷载比例因子[17]最大值作为评价指标进行对比,不同荷载路径下极限承载力对比如表2所示。从表2可以看出:7种荷载路径对应的极限承载力与荷载路径I得到的极限承载力的误差均在6%以内,可认为荷载路径对极限承载力没有影响。

(a) 荷载路径Ⅰ与荷载路径Ⅱ;(b) 荷载路径Ⅰ与荷载路径Ⅲ

表2 不同荷载路径下极限承载力对比
注:为增量分析时的荷载比例因子(LPF),分析时初始的弯矩、轴向压力和扭矩分别为1.85 kN·m,19.88 kN·m和1.42 kN·m;相似度取各种荷载路径的与路径I的之比。
4 压−弯−扭共同作用下构件弯矩作用平面内极限承载力分析
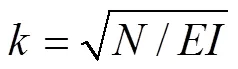
为进行参数化分析,对在压−弯−扭共同作用下的热轧圆钢管、焊接方钢管和焊接矩形钢管在内的270个模型进行分析,分析时模型一端固定一端自由,轴向集中荷载、扭矩和横向力通过点面耦合施加在自由端截面形心处。为了防止发生平面外失稳,在端部平面外方向上施加约束,初始几何缺陷的幅值依然为l/1 000,残余应力的分布形式参见文献[1]。钢材选取Q235钢。由于荷载路径对极限承载力没有影响,为了便于收敛,在分析时保持轴向压力和扭矩不变,逐渐增加横向力直至达到极限承载力。
4.1 圆钢管和方钢管
圆钢管的截面直径×壁厚为299 mm×16 mm,方钢管的截面边长×壁厚为300 mm×20 mm,分析选取的试件长细比分别为40,80,120和160。选取的恒定轴向压力分别为300,600,900,1 200和1 500 kN。选取的恒定扭矩分别为0,50,100,150,200和 250 kN·m。按照文献[7]中给出的分布形式分别对热轧圆钢管和焊接方钢管施加残余应力。同时,需要先对构件在轴心受压情况下的极限承载力进行分析以得到稳定系数。图9所示为分析得到的稳定系数曲线与GB 50017—2003“钢结构设计规范”[4]中标准柱子曲线(图中虚线)对比。由图9可知:分析所用模型的稳定系数曲线与文献[4]中柱子曲线a基本吻合。计算时采用的稳定系数如表3所示。
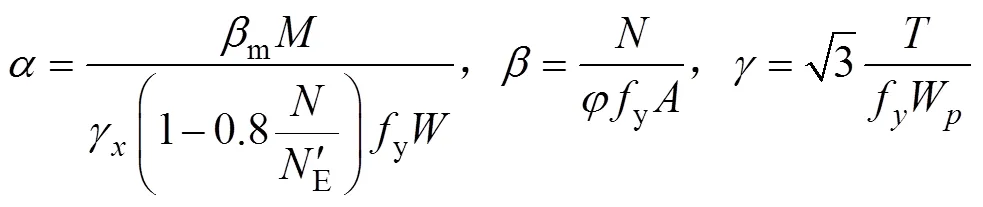
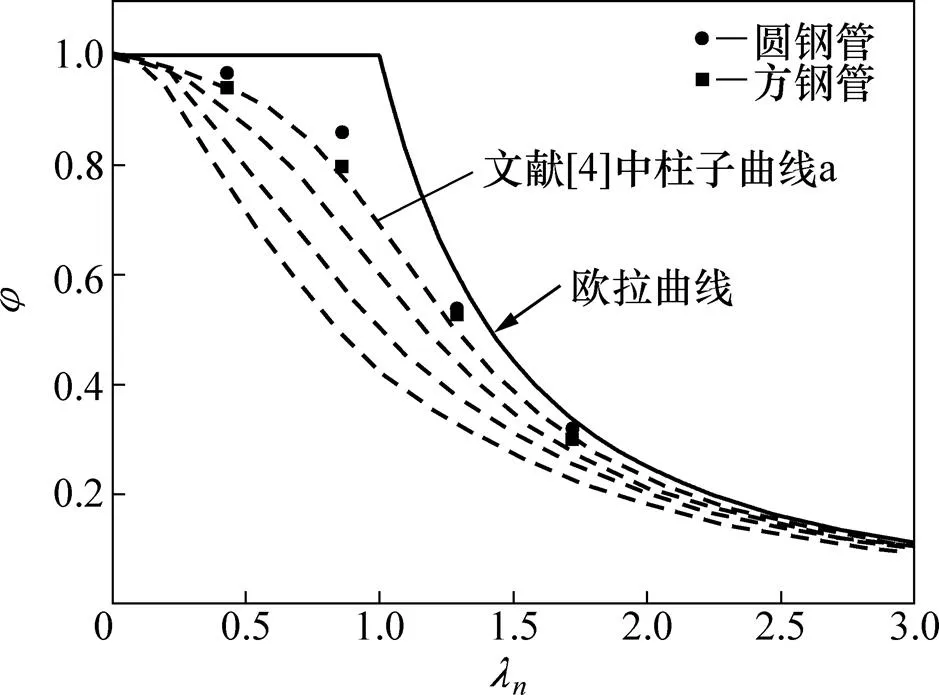
图9 柱子曲线对比

表3 稳定系数

4.2 矩形钢管
相比于等厚圆钢管与方钢管,矩形钢管很难保证板件宽度之比等于板件的厚度之比,在扭矩作用下截面往往会发生翘曲,因此,需要对扭矩作用下矩形截面压弯构件截面塑性发展的规律进行研究。对截面长×宽×壁厚为400 mm×300 mm×16 mm的箱形构件进行分析,材料特性、模型建立和分析方法与前面的相同。压−弯−扭共同作用下矩形截面构件塑性发展形式如图12所示。由图12(a)可知:截面塑性发展趋势相当于图2中的2种发展趋势叠加,具体可以表示为图12(b)中所示的3个区域,其中箭头表示塑性发展的方向。在塑性发展区域范围内,区域1的翘曲正应力正值和负值的分布关于纵轴对称即积分后结果为零,而区域2与区域3的翘曲正应力也可大部分相互抵消,因此,可以认为塑性发展开始时翘曲正应力对塑性发展只有促进作用(区域1的右半部分和区域3上部),之后对塑性发展有抑制作用(区域1的左半部分和区域2)和很弱的促进作用(区域3的下部),总体来说,区域2和3的塑性发展平均后仍可以近似认为是沿横向力作用方向均匀发展(见图12(a))。也就是说,翘曲正应力的存在只会使截面最危险点更早地进入塑性状态,而对截面最终承载能力的影响不大,因此,由式(15)和式(16)得到的设计方法依然适用。为了对这一理论进行进一步验证,本文对长细比为80和120的2类模型,选取恒定扭矩分别为0,150和300 kN∙m,共30个模型进行分析。
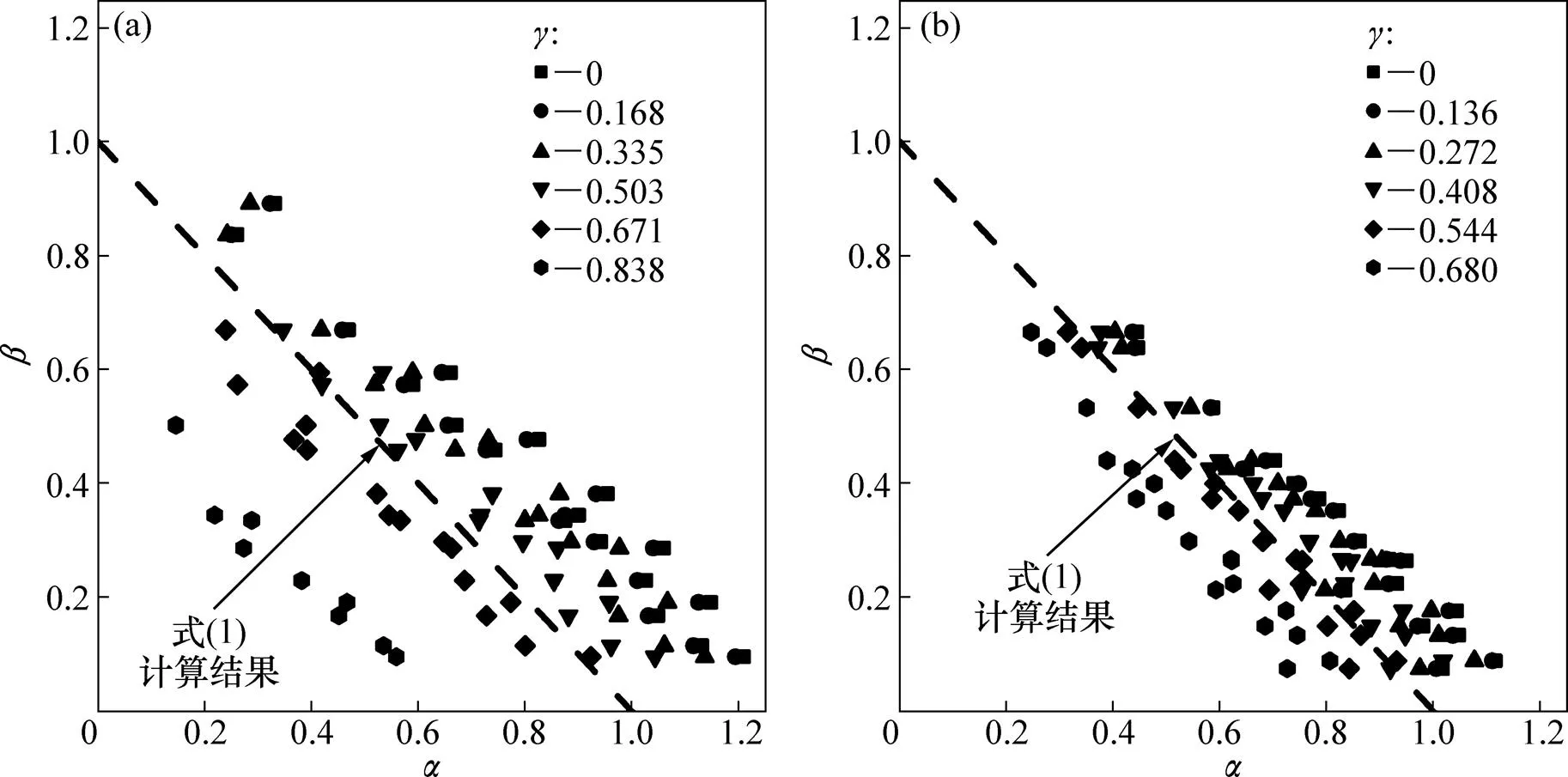
(a) 圆钢管;(b) 方钢管
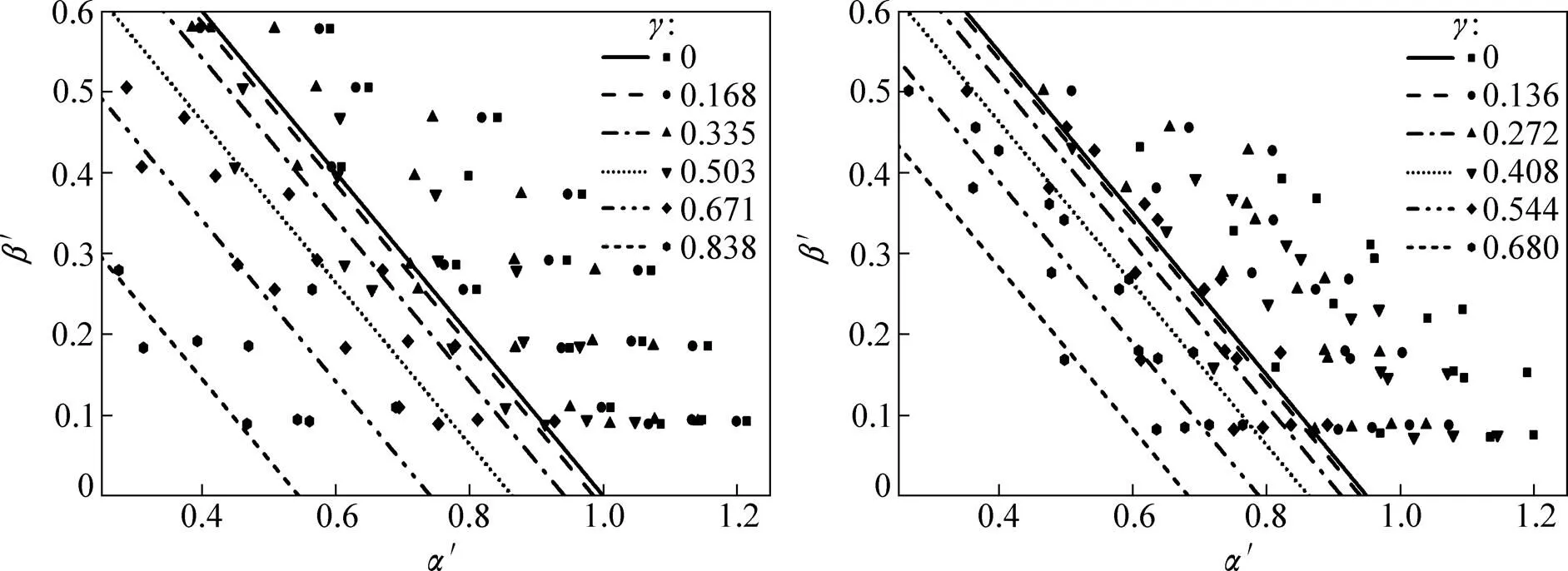
(a) 圆钢管;(b) 方钢管
针对矩形截面构件采用本文公式进行适用性验证所得结果见图13(其中,直线方程见式(15),数据点表示有限元分析结果)。由图13可知:式(15)同样能够很好地适用于在压−弯−扭共同作用下存在翘曲的矩形截面构件弯矩作用平面内极限承载力计算,证明了前文假设塑性发展理论的正确性。同时,考虑到结构工程中所使用的闭口截面构件多为圆钢管或包括方钢管在内的矩形截面钢管,因此,可以认为式(16)适用于在压−弯−扭共同作用下的闭口截面构件平面内承载力计算,并且具有较高的精度。此外,式(16)与现行GB 50017—2003“建筑钢结构设计规范”中的压弯构件弯矩作用平面内稳定设计公式在形式上一致,因而公式使用便捷。
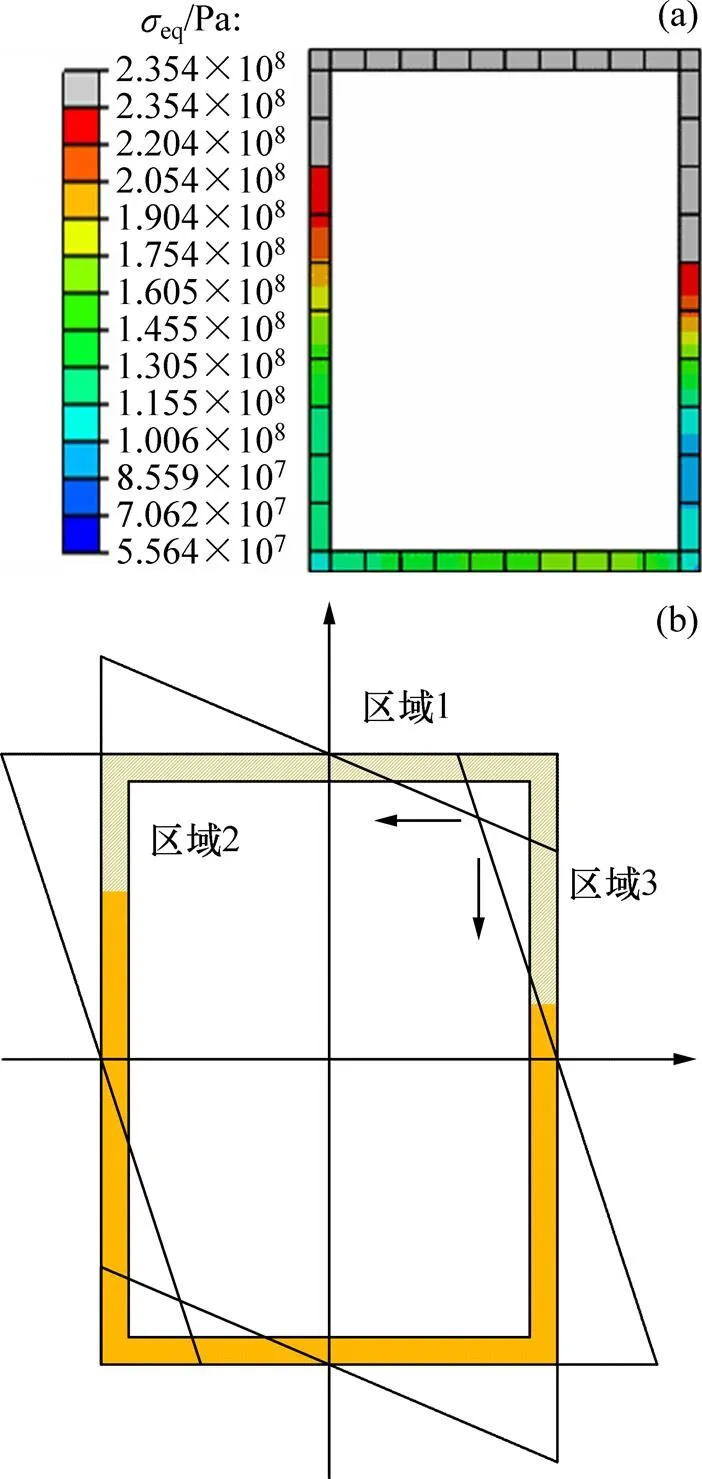
(a) 有限元结果;(b) 塑性发展趋势分析
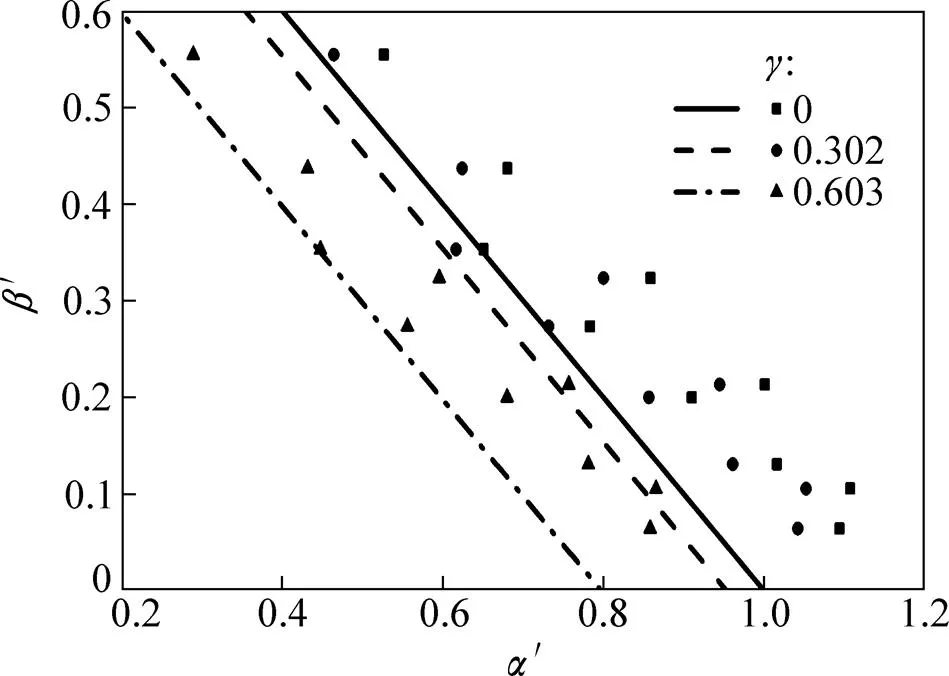
图13 针对矩形截面构件本文公式适用性验证
5 结论
1) 基于Umansky的闭口截面扭转理论和现行GB 50017—2003“建筑钢结构设计规范”压弯构件弯矩作用平面内稳定设计公式,推导出适用于压−弯−扭共同作用下闭口截面构件弯矩作用平面内极限承载力计算公式;该公式与现行规范中公式在形式上一致,在经验参数上能够共用,便于工程应用。
2) 通过量纲一的荷载比例因子分析压−弯−扭共同作用时冷弯矩形钢管所经历的7种荷载路径下的极限承载力,证明荷载路径对于构件的极限承载力几乎没有影响。
3) 大量数值模拟试验证明所提出的设计公式具有较高的精度;构件弯矩和轴向压力承载力随着扭矩增大降低,且降低程度越来越大。
4) 约束扭转的存在只会使截面最危险点更早进入塑性状态,而对截面最终的承载能力影响不大。根据自由扭转理论得出的设计公式对于存在约束扭转的矩形截面构件依然适用。
[1] 陈骥. 钢结构稳定——理论与设计[M]. 北京: 中国电力出版社, 2014: 118−141.CHEN Ji. Stability of steel structures and design[M]. China Electric Power Press, Beijing, 2014: 118−141.
[2] KIM K, YOO C H. Ultimate strengths of steel rectangular box beams subjected to combined action of bending and torsion[J]. Engineering Structures, 2008, 30(6): 1677−1687.
[3] 陈宜言, 林松, 尧国皇. 圆形钢管弯扭构件承载力实用计算方法研究[J]. 特种结构, 2012, 29(2): 102−105, 115.CHEN Yiyan, LIN Song, YAO Guohuang. Research on the behavior of steel tubular members with circular sections subjected to bending and torsion[J]. Special Structures, 2012, 29(2): 102−105, 115.
[4] GB 50017—2003, 钢结构设计规范[S]. GB 50017—2003, Code for design of steel structures[S].
[5] GB 50018—2002, 冷弯薄壁型钢结构技术规范[S]. GB 50018—2002, Technical specification for cold-formed thin-walled steel structures[S].
[6] AISC 360-12. Specification for structural steel building[S].
[7] 陈骥. 受轴压、双向弯曲和扭矩作用的两端简支工形截面压弯构件的稳定设计[J]. 建筑钢结构进展, 2010, 12(3): 7−13. CHEN Ji. Stability design of simply supported i-section beam-columns under axial compression, biaxial bending and torsion[J]. Progress in Steel Building Structures, 2010, 12(3): 7−13.
[8] 罗尧治, 张冰, 季伟捷, 等. 双锥型变截面矩形钢管的试验研究及承载力分析[J]. 土木工程学报, 2006, 39(9): 8−16.LUO Yaozhi, ZHANG Bing, JI Weijie, et al. Experimental study and capacity analysis of double-tapered rectangular steel tubes[J]. China Civil Engineering Journal, 2006, 39(9): 8−16.
[9] 曹哲玮. 箱型钢结构于三维载重下之承载行为[C]. 海峡两岸地震工程青年学者研讨会. 上海, 2010: 178−181. CAO Zhewei. Ultimate strength of hollow steel box sections under combined three-dimensional load[C]. Symposium of young scholars and on seismic engineering between the two sides of the Taiwan Straits. Shanghai, 2010: 178−181.
[10] 田兴运. 扭矩对受弯和压弯钢构件整体稳定性的影响[J]. 工程力学, 2010, 27(6): 106−112. TIAN Xingyun. The impact of torsions on the overall stability of curved and compressed steel members[J]. Engineering Mechanics, 2010, 27(6): 106−112.
[11] 黄宏, 朱琪, 陈梦成, 等. 方中空夹层钢管混凝土压弯扭构件试验研究[J]. 土木工程学报, 2016, 49(3): 91−97. HUANG Hong, ZHU Qi, CHEN Mengcheng, et al. Experimental study on concrete filled double-skin square steel tubes under compression-bending-torsion loading conditions[J]. China Civil Engineering Journal, 2016, 49(3): 91−97.
[12] 吴丽珠, 朱琪, 黄宏, 等. 方中空夹层钢管混凝土压弯扭构件承载力计算方法探讨[J]. 南昌大学学报(工科版), 2015, 37(3): 257−261. WU Lizhu, ZHU Qi, HUANG Hong, et al. Load carrying capacity of concrete filled double skin square steel tubes under compression-bending-torsion loading conditions[J]. Journal of Nanchang University (Engineering & Technology), 2015, 37(3): 257−261.
[13] 徐玉野, 何叶, 罗漪, 等. 压扭作用下钢筋混凝土L形柱的抗扭承载力[J]. 中南大学学报(自然科学版), 2014, 45(3): 932−938.
XU Yuye, HE Yei, LUO Yi, et al. Ultimate torque of reinforced concrete Lshaped columns under combined axial force and torque. Journal of Central South University (Science and Technology), 2014, 45(3): 932−938.
[14] 蔡春声, 王国周. 加载途径对钢压弯构件稳定极限承载力的影响[J]. 建筑结构学报, 1992, 13(3): 19−28. CAI Chunsheng, WANG Guozhou. The effect of load paths on the stability bearing capacity of compression-bending steel members[J]. Journal of Building Structures, 1992, 13(3): 19−28.
[15] 包世华, 周坚. 薄壁杆件结构力学[M]. 北京: 中国建筑工业出版社, 2006: 91−132.BAO Shihua, ZHOU Jian. Structural mechanics of thin-walled member[M]. Beijing: China Architecture & Building Press, 2006: 91−132.
[16] 丁阳. 钢结构设计原理[M]. 2版. 天津: 天津大学出版社, 2011: 239−271. DING Yang. Design principle of steel structure[M]. 2nd ed. Tianjin: Tianjin University Press, 2011: 239−271.
[17] ABAQUS Inc. ABAQUS Analysis user’s manual [EB/OL]. 2017-6-10 http://dsk.ippt.pan.pl/docs/abaqus/v6.13/books/usb/de fault.htm
[18] KEY P W, HANCOCK G J. A theoretical investigation of the column behaviour of cold-formed square hollow sections[J]. Thin-Walled Structures, 1993, 16(1/4): 31−64.
[19] 王登峰, 贾文文, 王元清, 等. 初始缺陷对除尘器壳体立柱轴压稳定性的影响[J]. 中南大学学报(自然科学版), 2016, 47(8): 2810−2819.
WANG Dengfeng, JIA Wenwen, WANG Yuanqing, et la. Influence of initial imperfection on stability of axially compressed column in electrostatic precipitator casing. Journal of Central South University (Science and Technology), 2016, 47(8): 2810−2819.
[20] 陈绍蕃, 申红侠, 冉红东, 等. 钢压弯构件面内等效弯矩系数取值的改进(下)——端部有侧移的构件[J]. 建筑钢结构进展, 2010, 12(5): 8−12. CHEN Shaofan. Improvement of the equivalent moment factor for in-plane stability calculation of steel beam-columns part (II): members supported at both ends[J]. Progress in Steel Building Structures, 2010, 12(5): 8−12.
(编辑 伍锦花)
In-plane ultimate strength of closed section steel members subjected to combined compression, bending and torsion
HAN Qinghua1, 2, CHENG Yuhao1, LU Yan1, 2
(1. School of Civil Engineering, Tianjin University, Tianjin 300072, China; 2. Key Laboratory of Coast Civil Structure Safety of Ministry of Education, Tianjin University, Tianjin 300072, China)
To obtain the in-plane ultimate strength of closed section members subjected to combined compression, bending and torsion, a new design method was proposed based on Umansky’s torsion theory and code for GB 50017—2003 “Design of steel structures”. The ultimate strengths of in-plane buckling of closed section members subjected to combined compression, bending and torsion were analyzed by numerical analysis. The geometric initial imperfection and residual stress were taken into account when modeling and the nonlinearity of material and geometric were also taken into account. The results show that the proposed design method is suitable for the closed section members subjected to combined compression, bending and torsion. It reflects the real loading conditions and is also easy to be used. Seven kinds of load paths caused by combined compression, bending and torsion have little effect on the ultimate strength of models, and the design method has high accuracy. The bearing capacity of compression and bending decreases when torque increases, and this effect increases with the increase of torque. Restrained torsion causes the change of early plastic development while it has little influence on the ultimate strength of the rectangular box columns. Therefore, the design method based on free torsion theory is also suitable for the rectangular box columns under combined compression, bending and torsion.
combined compression, bending and torsion; closed section steel members; in-plane ultimate strength; restrained torsion; load path
TU391
A
1672−7207(2018)08−2039−11
2017−08−12;
2017−09−29
国家重点研发计划项目(2016YFC0701103);国家自然科学基金资助项目(51525803);天津市建设系统科学技术发展计划项目(2014)(Project(2016YFC0701103) supported by the National Key Research and Development Plan of China; Project(51525803) supported by the National Natural Science Foundation of China; Project(2014) supported by the Scientific and Technological Development Plans of Tianjin Construction System)
芦燕,博士,副教授,从事钢结构与空间结构研究;E-mail:yanlu86@tju.edu.cn
10.11817/j.issn.1672−7207.2018.08.026
