基于干扰观测器的盾构推进系统非线性控制
2018-09-07李明杰魏建华方锦辉
李明杰,魏建华,方锦辉
基于干扰观测器的盾构推进系统非线性控制
李明杰,魏建华,方锦辉
(浙江大学 流体动力与机电系统国家重点实验室,浙江 杭州,310027)
为了提高盾构推进系统在复杂地质中进行隧道掘进的精度和稳定性,提出1种基于干扰观测器、同时考虑推进液压系统中的模型不确定性和外部干扰非线性控制算法。建立推进系统的动力学模型,并通过反步设计法的李雅普若夫方程证明控制系统的稳定性。通过MATLAB和AMESim联合仿真以及MATLAB Simulink实时系统下的实验验证控制算法的有效性。研究结果表明:相比于传统PID控制算法,本文提出的控制算法的控制精度和抗干扰能力均有较大提高。
盾构;干扰观测器;非线性控制;反步设计法;李雅普若夫方程
随着社会经济的发展,地下空间的开发利用已经成为城市和区域交通建设的重要领域。盾构系统具有安全、高效、环保及自动化程度高等诸多优点,因此被广泛应用于铁路、公路、市政、供水、供气、防洪、水电等隧道工程建设[1]。盾构掘进机的主要组成部分包括刀盘及其驱动系统、推进系统、管片拼装机、排渣机构、导向系统等[2−3]。推进系统是盾构掘进机的关键子系统,需要实现压力控制、速度控制、姿态控制,决定着隧道设计线路的施工质量。由于地下施工条件复杂,推进系统必须能够适应不同地质情况,并提供合理的推进力和推进速度。推进系统目前广泛采用比例阀控油缸系统以及比例−积分−微分(PID)控制策略,在地质条件单一的地层中施工效果较好,但在地质条件复杂的地层中往往会减缓施工进度,产生蛇形,甚至超过误差要求。液压系统中存在较强的非线性以及外部干扰,导致采用传统控制策略无法取得较好的控制效果。为了提高液压系统的控制精度和抗干扰能力,许多非线性控制策略被应用到液压控制系统中。反馈线性化[4−5]将非线性的液压系统线性化,并能根据线性系统设计控制器。滑模控制器[6−7]的应用能够消除系统不确定性和外部干扰带来的影响,但同时也容易引起系统高频颤振,降低控制效果。自适应控制[8−9]始于高性能飞行器自动驾驶研究。自适应控制器能够实现参数在线估计和实时调整,但抗扰动能力不强。干扰观测器[10−15]能够很好地克服系统中出现的负载扰动和模型不确定性。由于实际盾构推进系统中负载很难被测量,无法实现对负载的实时补偿,致使控制效果下降,而干扰观测器恰好能够解决这个问题。本文作者通过建立推进系统的动力学模型,设计干扰观测器,对比例溢流阀模拟的负载进行实时观测估计。通过仿真和实验的方法研究基于干扰观测器的非线性控制策略(DOBC)在控制精度和抗干扰能力上的有效性。
1 推进系统建模
图1所示为盾构推进系统单缸液压原理图。其中推进油缸与加载油缸通过质量块连接,推进油缸由比例伺服阀控制,加载油缸由比例溢流阀控制。在实际运动过程中,通过给比例溢流阀施加一定信号加载,同时给定位移指令,通过控制比例伺服阀实现推进油缸位移的精确控制(其中,L为加载油缸加载腔压力;s为系统供油压力;t为系统回油压力)。
推进油缸的力平衡方程为

式中:1为推进油缸作用腔压力;1为推进油缸油液作用面积;L为加载油缸所施加的负载力;为负载等效质量;为重力加速度;为外部干扰(包括摩擦力、黏性阻力等);L为推进油缸位移。
由于在盾构实际施工中负载无法实时测量,故将负载与系统干扰进行集中处理,其表达式如下:

推进油缸的流量连续性方程为

式中:1为推进油缸作用腔流量;t为推进油缸总泄露系数;0为推进油缸初始容积;为油液弹性模量。
比例伺服阀阀口流量压差为
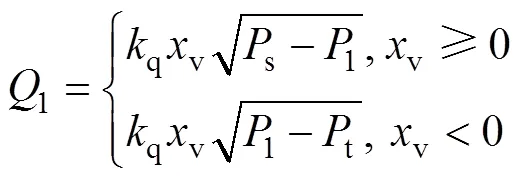
式中:q为比例伺服阀流量增益;v为比例伺服阀阀芯位移。
由于液压系统的频响与比例伺服阀的频响相比小得多,所以忽略比例伺服阀的动态响应,将其视为如下比例环节:
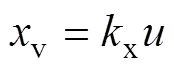
式中:x为比例增益系数;为比例伺服阀控制指令。
定义系统状态变量为
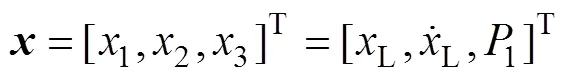
由式(1)~(5)得到系统状态方程如下:
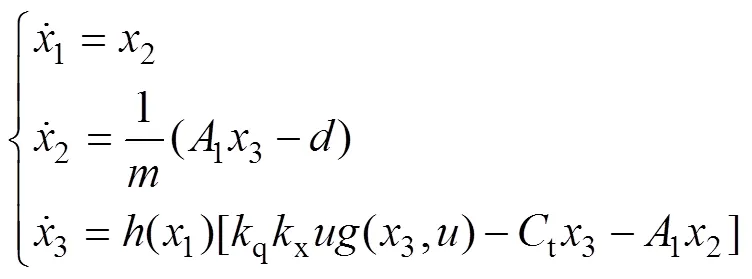
式中:
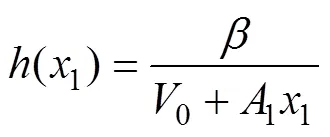
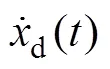
2 控制器设计
为使液压推进系统能够在复杂的地质情况下实现对指令位移的准确跟踪,设计观测器补偿外部负载干扰和系统自身模型不确定性。
2.1 干扰观测器设计
所提出的干扰观测器建立在状态变量2的基础之上,观测器方程表达式如下:
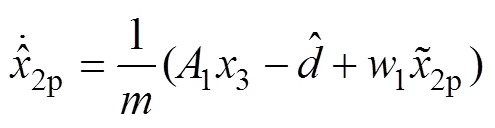

选择如下自适应率:

式中:1为正常数;为额外的修正项,用以保证整个闭环控制系统的稳定性。
定义李雅普若夫函数1为

将1对时间求导,并代入式(8)和(9)可得

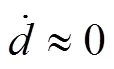
2.2 非线性位移控制器设计
非线性控制器由外部位移闭环和内部压力闭环构成,并采用反步设计方法。
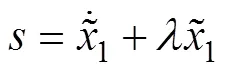
式中:为正常数。
将式(12)两边对时间求导,并代入式(6)可得
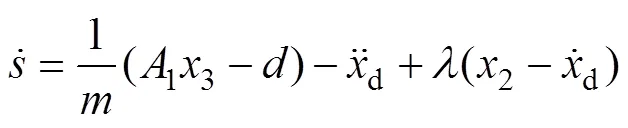
将3作为式(13)的虚拟控制输入,设3的虚拟控制输入3为
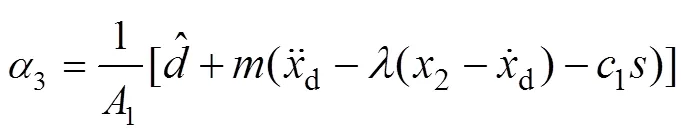
式中:1为正常数。
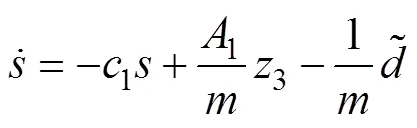
定义李雅普若夫函数2为

式中:2为正常数。
将2对时间求导,并代入式(11)和(15)可得
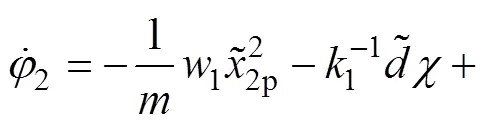
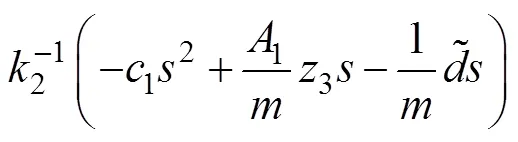
故令
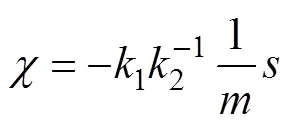
将式(18)代入式(17)可得
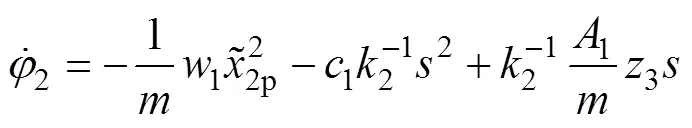
第2步,将3对时间求导可得:
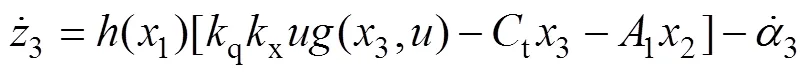
故设计实际控制输入为

式中:2和3均为正常数。
将式(21)代入式(20)可得

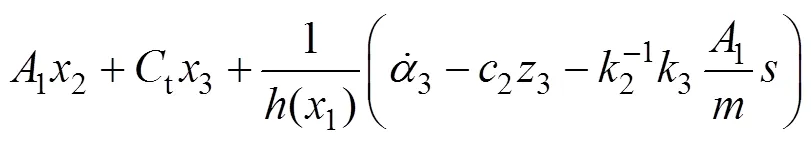

则

定义李雅普若夫函数3为
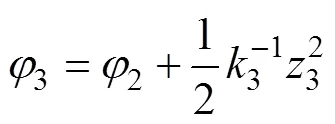
将3对时间求导,并代入上述式(19)和(22)可得
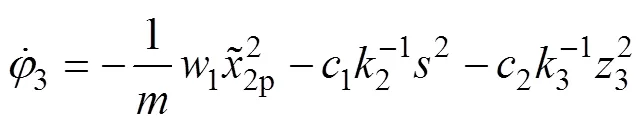
设计基于干扰观测器的非线性控制器(DOBC)的稳定性得到了证明,且系统稳定后位移跟踪误差趋于0 mm。
3 仿真分析
为了验证本文所提出算法的有效性,采用MATLAB和AMESim联合仿真的办法进行仿真验证。系统采用比例溢流阀(最大溢流压力为21 MPa)加载的方式模拟盾构推进过程中的负载。
图2所示为位移指令信号曲线。

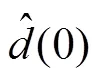
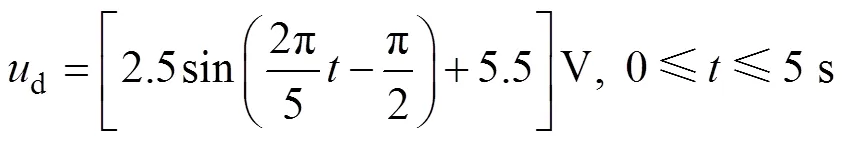
3种不同工况下的位移跟踪误差仿真结果分别如图4~6所示。由图4~6可知:当负载不变或变化频率较小时,位移跟踪误差均保持在±0.02 mm之内。
即使在负载突变的情况下,仅在突变瞬间位移跟踪误差增大到−0.8~0.5 mm,其余时刻均能保持在 ±0.02 mm之内。由此可见,在仿真条件下,DOBC控制算法在负载变化较慢以及突变时均有较好的控制效果,可以有效地抑制因负载变化而引起的控制效果 下降。
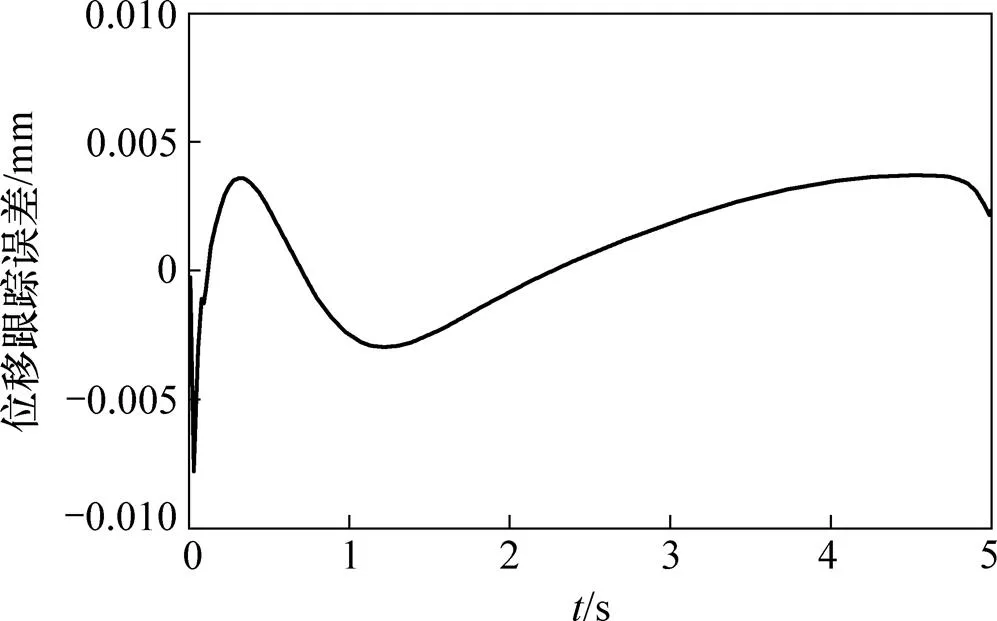
图3 比例溢流阀电压指令为3 V时位移跟踪误差

表1 推进系统参数和DOBC控制器参数
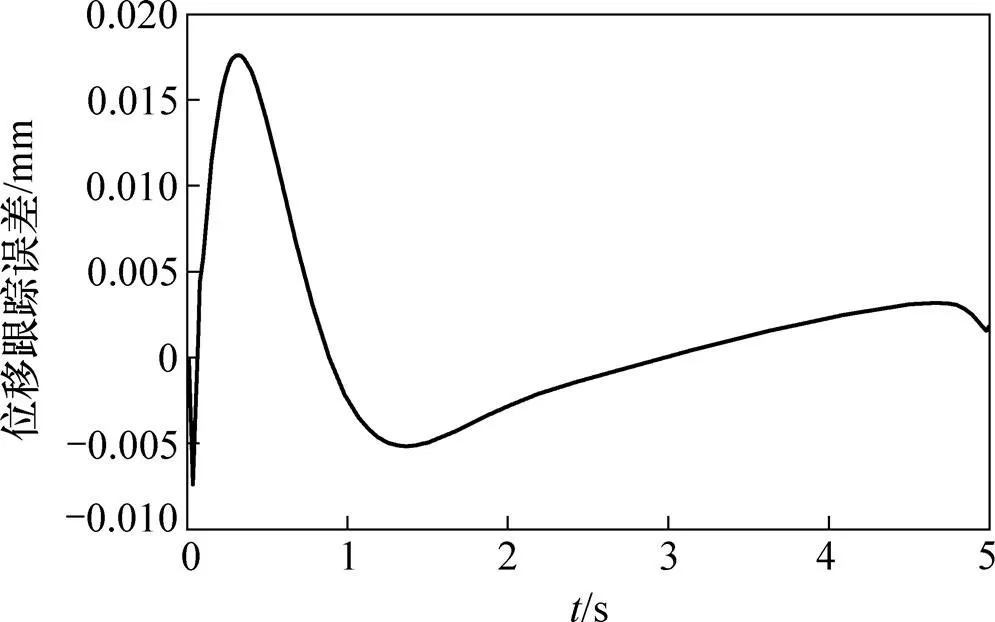
图4 比例溢流阀电压指令为8 V时位移跟踪误差
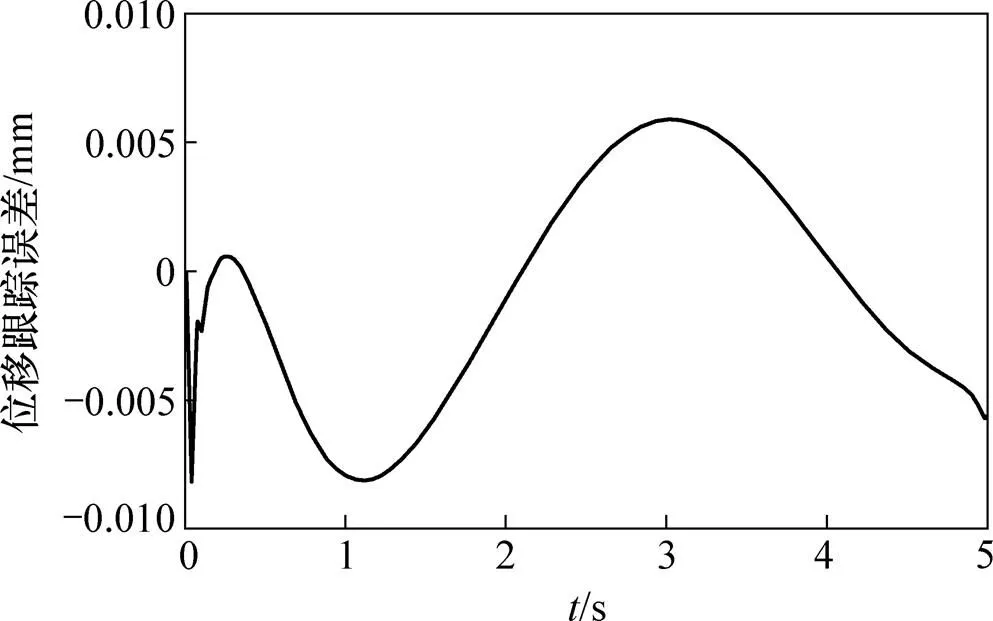
图5 比例溢流阀电压指令为正弦信号时位移跟踪误差

图6 比例溢流阀电压指令为阶跃信号时位移跟踪误差
4 实验分析
搭建实验平台进一步验证所提出的DOBC控制算法的有效性。实验平台建立在MATLAB Simulink实时系统的基础上,实验平台框架结构如图7所示。实验元件型号及参数见表2。
为了更好地说明DOBC控制算法的控制效果,将其与传统使用的PID控制算法进行对比。同样,PID控制算法的参数是在恒定负载的工况下(比例溢流阀

图7 实验平台框架图

表2 实验元件型号及参数
电压指令为3 V)整定完成,控制器方程表达式如下:

不同工况下PID及DOBC控制算法位移跟踪误差实验结果分别如图8~12所示。由图8~12可知:PID控制算法在恒定负载下可以达到±1.2 mm的跟踪精度,DOBC控制算法可以达到±0.03 mm的跟踪精度。虽然实验中采用比例溢流阀加载,负载依然存在一定变化,但DOBC控制算法能够补偿负载变化,所以,可以得到高的控制精度。此外,PID控制算法在负载变化后控制精度明显下降,位移跟踪精度从±1.2 mm下降到±2.5 mm;而DOBC在负载变化时,控制精度基本保持稳定,除初始阶段和负载阶跃突变时以外,其余时刻仍可以维持在±0.03 mm之内。
1—比例溢流阀指令为3 V;2—比例溢流阀指令为8 V; 3—比例溢流阀指令为正弦信号; 4—比例溢流阀指令为阶跃信号。
图8 PID控制策略实验位移跟踪误差
Fig. 8 Experimental tracking errors of PID controller

图9 比例溢流阀电压指令为3 V时DOBC控制策略的实验位移跟踪误差
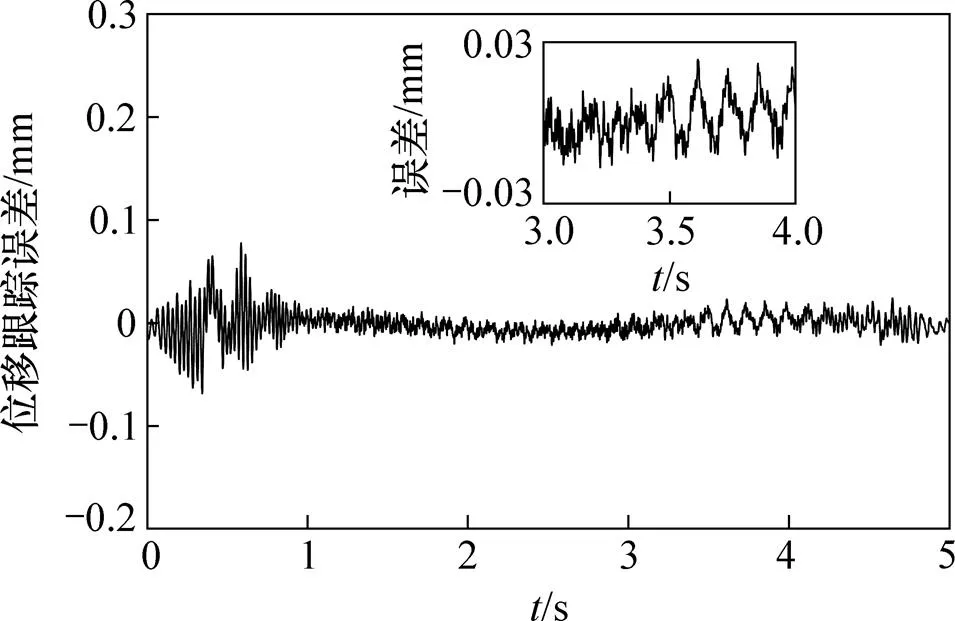
图10 比例溢流阀电压指令为8 V时DOBC控制策略的实验位移跟踪误差
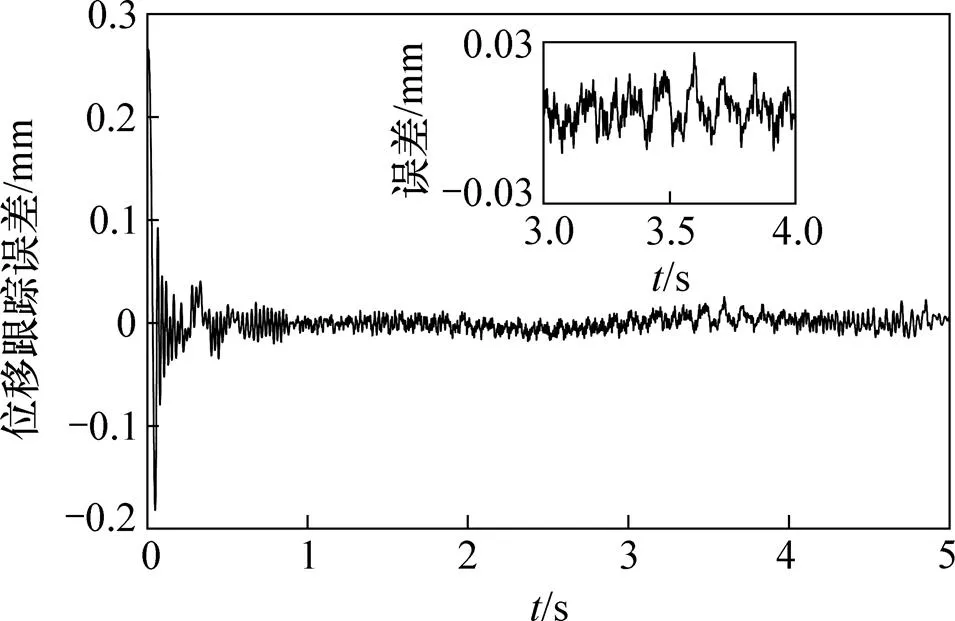
图11 比例溢流阀电压指令为正弦信号时的DOBC控制策略实验位移跟踪误差
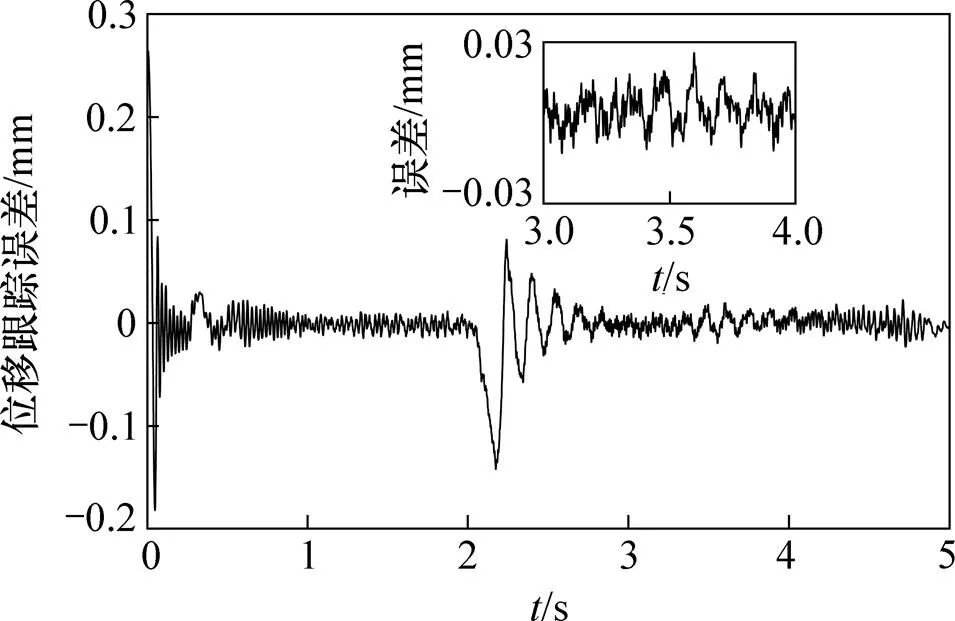
图12 DOBC控制策略比例溢流阀电压指令为阶跃信号时实验位移跟踪误差
在初始阶段,由于干扰观测器初始值还未趋近负载的实际值,负载估计存在误差,故而初始误差比稳定状态下的大。负载突变阶段的误差增大同样是上述原因造成的。
5 结论
1) 通过李雅普若夫方程证明本文所提出的DOBC控制算法具有较好的稳定性和动态性能。
2) 与传统PID控制算法相比,DOBC控制算法在负载缓慢变化和突变的情况下,均有着很高的位移控制精度。
3) 该算法在盾构推进系统中有着潜在的应用价值,干扰观测器对负载的估计可以克服盾构推进过程中负载多变且无法测量的问题。
[1] 王梦恕. 中国盾构和掘进机隧道技术现状、存在的问题及发展思路[J]. 隧道建设, 2014, 34(3): 179−187. WANG Mengshu. Tunneling by TBM/shield in China: state-of-art, problems and proposals[J]. Tunnel Construction, 2014, 34(3): 179−187.
[2] MAIDL B, SCHMID L, RITZ W, et al. Hardrock tunnel boring machines[M]. Berlin, Germany: John Wiley & Sons, 2008: 16−19.
[3] MAIDL B, HERRENKNECHT M, MAIDL U, et al. Mechanised shield tunnelling[M]. 2nd ed. Berlin, Germany: John Wiley & Sons, 2013: 1−23.
[4] VOSSOUGHI G, DONATH M. Dynamic feedback linearization for electrohydraulically actuated control systems[J]. Journal of Dynamic Systems, Measurement, and Control, 1995, 117(4): 468−477.
[5] SEO J, VENUGOPAL R, KENN J P. Feedback linearization based control of a rotational hydraulic drive[J]. Control Engineering Practice, 2007, 15(12): 1495−1507.
[6] KACHROO P, TOMIZUKA M. Chattering reduction and error convergence in the sliding-mode control of a class of nonlinear systems[J]. IEEE Transactions on Automatic Control, 1996, 41(7): 1063−1068.
[7] GUAN Chen, PAN Shuangxia. Adaptive sliding mode control of electro-hydraulic system with nonlinear unknown parameters[J]. Control Engineering Practice, 2008, 16(11): 1275−1284.
[8] KRSTIC M, KANELLAKOPOULOS I, KOKOTOVIC P V. Nonlinear and adaptive control design[M]. New York, USA: John Wiley & Sons, 1995: 1−17.
[9] AHN K K, NAM D N C, JIN M. Adaptive backstepping control of an electrohydraulic actuator[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(3): 987−995.
[10] CHEN Wenhua. Disturbance observer based control for nonlinear systems[J]. IEEE/ASME Transactions on Mechatronics, 2004, 9(4): 706−710.
[11] GUO Kai, WEI Jianhua, FANG Jinhui, et al. Position tracking control of electro-hydraulic single-rod actuator based on an extended disturbance observer[J]. Mechatronics, 2015, 27: 47−56.
[12] PI Yangjun, WANG Xuanyin. Observer-based cascade control of a 6-DOF parallel hydraulic manipulator in joint space coordinate[J]. Mechatronics, 2010, 20(6): 648−655.
[13] KIM W, SHIN D, WON D, et al. Disturbance-observer-based position tracking controller in the presence of biased sinusoidal disturbance for electrohydraulic actuators[J]. IEEE Transactions on Control Systems Technology, 2013, 21(6): 2290−2298.
[14] YAO Jianyong, DENG Wenxiang. Active disturbance rejection adaptive control of hydraulic servo systems[J]. IEEE Transactions on Industrial Electronics, 2017, 64(10) 8023−8032.
[15] LI Shizhen, GUO Kai, ZHU Wule. Nonlinear robust prediction control of hybrid active-passive heave compensator with extended disturbance observer[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6684−6694.
(编辑 伍锦花)
Nonlinear control of tunnel boring machine thrust system based on disturbance observer
LI Mingjie, WEI Jianhua, FANG Jinhui
(State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou 310027, China)
To improve accuracy and stability of tunnel boring machine(TBM) thrust system that works under complicated geological conditions, nonlinear control strategy which takes both model uncertainties and external perturbations into consideration was proposed based on the disturbance observer. Dynamics model of the system was derived and stability of the overall closed-loop system was verified via backstepping based on Lyapunov theory. Validity of the proposed strategy was proved by MATLAB and AMESim co-simulation and by experiment conducted in MATLAB Simulink real-time system. The results show that compared with traditional PID strategy, the proposed strategy has better performance not only in control accuracy but also in perturbation attenuation.
tunnel boring machine(TBM); disturbance observer; nonlinear control; backstepping; Lyapunov theory
TH137
A
1672−7207(2018)08−1922−07
10.11817/j.issn.1672−7207.2018.08.012
2017−08−06;
2017−09−24
国家高技术研究发展计划(863计划)项目(2012AA041804) (Project(2012AA041804) supported by the National High Technology Research and Development Program (863 Program) of China)
魏建华,博士,教授,从事电液控制理论及应用研究;E-mail:jhwei@zju.edu.cn
