强降雨条件下考虑渗透力影响的粗粒土高路堤边坡稳定性
2018-09-07段旭龙何忠明王保林
段旭龙,何忠明,王保林
强降雨条件下考虑渗透力影响的粗粒土高路堤边坡稳定性
段旭龙1,何忠明2,王保林2
(1. 中南大学 地球科学与信息物理学院,湖南 长沙,410083;2. 长沙理工大学 交通运输工程学院,湖南 长沙,410114)
为了分析强降雨条件下粗粒土高路堤边坡的稳定性,基于渗透力理论,对边坡在强降雨条件下的二维渗流特性进行计算,然后,通过Fish语言编程,将边坡孔隙水压力和渗透力等渗流参数导入FLAC3D软件中,重点分析渗透力变化对路堤边坡稳定性的影响。研究结果表明:在强降雨条件下,路堤边坡在方向的渗流梯度在边坡表面及第二级边坡坡脚处表现为正值,坡脚处包络线所包围的正值区域逐渐向边坡内部扩展,边坡坡顶处在和方向的渗流梯度的变化幅度较大;路堤边坡表层孔隙水压力随降雨入渗持续而逐渐增加,随雨水的不断渗出而逐渐减小;路堤边坡坡顶处体积含水率呈现“凸”型分布,边坡纵截面体积含水率呈现“凹”型分布;随着雨水持续入渗,路堤边坡塑性区首先在各级边坡坡脚处及第二级边坡坡脚下方形成,并逐渐沿坡顶方向向边坡内部扩展,形成塑性贯通区;受渗透力的影响,边坡安全系数演变规律分为缓慢上升阶段、缓慢下降阶段、快速下降阶段和缓慢回升阶段。
强降雨;粗粒土;稳定性;渗透力;安全系数
高速公路的大规模修建,极大地推动了我国交通及经济建设的迅速发展,但也在一定程度上改变了当地局部环境。其中,改变最典型的是对自然地形进行了深挖或高填,形成了高低不同、坡度各异的工程边坡,改变了当地原有的应力场,严重影响了道路运营及行车安全。为此,国内外相关学者针对边坡的稳定性进行了大量研究,如:刘俊新等[1]基于流固耦合作用原理,建立了边坡非饱和区的流固耦合方程,计算了流固耦合作用下边坡的稳定性,并认为降雨影响了边坡失稳的范围、深度及程度;徐平等[2]以三峡库区马家沟附近1个失稳边坡为例,建立了相应的数值分析模型,并基于强度折减法,计算了边坡在1个水文周期内水库水位高程变化对边坡安全系数的影响;MEIN等[3]通过调研边坡实际工程概况,依托工程边坡条件,分析了边坡在降雨入渗条件下的作用机理,对积水前、后的边坡入渗率公式进行了推导,最后运用数值软件对边坡稳定性进行了计算,揭示了土坡在降雨入渗条件下的稳定性变化规律;DUNKERLEY[4]提出了一种入渗坡面非稳态的分析方法,并利用该方法研究了降雨强度变化幅度对坡面径流产生条件的影响,分析了边坡稳定性;张卢明等[5]考虑了降雨及地下水位线对边坡稳定性的影响,认为边坡基质吸力受降雨强度的影响较大,边坡稳定性对降雨强度较敏感。从上述研究中可见降雨是诱发边坡失稳的最直接因素,这些研究者针对降雨这一因素对边坡的稳定性进行了大量研究,但很少考虑降雨入渗条件下渗透力作用对边坡稳定性的影响。渗透力作为引起土体渗透变形的动力,其变化将直接影响边坡的破坏程度。为此,本文作者在总结前人研究边坡稳定性成果的基础上,以粗粒土高路堤边坡为研究对象,基于饱和—非饱和渗流理论,计算边坡在强降雨条件下的二维渗流特性,然后,将边坡渗透力和孔隙水压力等渗流结果通过Fish语言导入到FLAC3D软件中,计算降雨入渗条件下粗粒土高路堤边坡的稳定性,以便为工程边坡防护及排水设计提供理论参考。
1 稳定性分析理论基础
1.1 饱和−非饱和渗流理论
粗粒土高路堤边坡在降雨入渗条件下的渗流特性满足达西定律[6]:

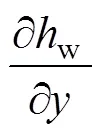
在边坡饱和区内,土体的渗透系数一般为定值,但在非饱和区内,由于体积含水率不同,导致边坡渗透系数表现出随基质吸力增加而增加,其饱和−非饱和渗流控制微分方程为[6]
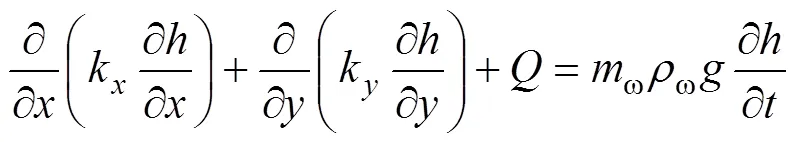
式中:为土体中的总水头;k和k分别为和方向的渗透系数;为源汇项;ω为比水容量;ω为水的密度;为重力加速度;为时间。
土水特征曲线是反映边坡饱和−非饱和状态下体积含水率与基质吸力之间的特定关系。为分析这种特定的关系,FREDLUND 等[7]进行了大量的渗流试验,认为土水特征曲线为对数函数的幂函数形式,虽然适用范围较广,但由于其分析过程复杂,影响因素较多,并没有广泛应用于岩土体的渗流分析中;RAHARDJO等[8]根据大量渗流试验结果,拟合了土水特征曲线的幂函数形式。这种形式参数简单,拟合效果符合试验结果,得到了广泛应用。其具体方程为
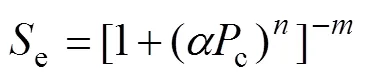
式中:c为基质吸力;,和为拟合参数。参数和之间存在=(1−)−1的关系,代入式(3)可得
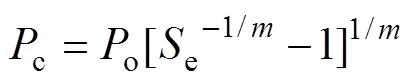
式中:o=1/;e为有效饱和度。
1.2 渗透力理论
渗透力是指土体中水的流动对土骨架颗粒所施加的作用力[9−12]。在强降雨条件下,雨水在粗粒土高路堤边坡表面入渗,继而向边坡内部拓展,形成渗流。在雨水渗流过程中,雨水的流动对粗粒土骨架形成了拖拽力,其作用效果如图1所示。

图1 渗透力作用示意图
在降雨入渗条件下,粗粒土骨架受水流作用的静力平衡方程为:
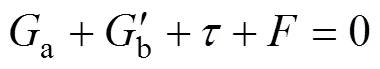

式中:a为水上部分自重力;b′为水下部分浮重力;为抗剪强度;为渗透力合力;s为饱和重度;w为水的重度;为水位线以下粗粒土体积。粗粒土高路堤边坡在强降雨条件下和方向的渗流梯度,可采用Geo-stduio软件的seep模块进行模拟计算,然后将计算结果乘以相应的水的重度w得到渗透力,其为和方向2个力的合力,具体计算公式为[13−14]:

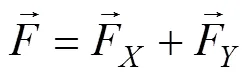
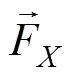
1.3 稳定性抗剪强度理论
在自然条件下,粗粒土高路堤边坡由于地下水的存在,处于一种饱和−非饱和的静态稳定状态。降雨入渗后,边坡饱和区和非饱和区进行了重分布,破坏了边坡原有的静态稳定性,使边坡的稳定性处于一种动态变化过程中。其饱和区的饱和抗剪强度f满足[15−17]
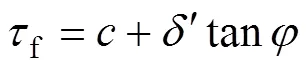
式中:为黏聚力;′为剪切滑裂面的有效正应力;为内摩擦角。
式(9)仅考虑了饱和状态下粗粒土骨架的抗剪强度,未考虑非饱和状态下孔隙水压力对边坡渗流及稳定性的贡献。为此,FREDLUND等[7]针对现有饱和抗剪强度公式的不足,根据非饱和土的双应力变量(−a,a−w)理论提出非饱和抗剪强度公式:
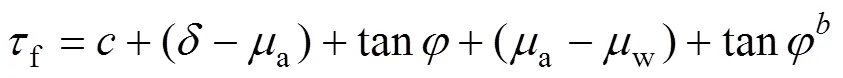
式中:a为边坡粗粒土骨架的进气值,考虑边坡孔隙与大气相连,a=0;b为基质吸力对内摩擦角的作用,按经验取值b=14°;w为孔隙水压力。
2 二维渗流特性分析
2.1 二维渗流计算模型及参数
二维渗流计算模型如下:某高速公路在施工过程中形成了高度约20 m的粗粒土高路堤边坡,该边坡分2级放坡,其中,第1级坡高8 m,坡率为1:1.50;第2级坡高12 m,坡率为1:1.75;2级边坡交接处平台宽2 m。为了研究强降雨条件下该粗粒土高路堤边坡的二维渗流特性,以该路堤横断面的一半为研究对象,建立二维渗流计算模型,如图2所示。为同时考虑计算精度与计算时步,将模型划分为2 342个节点和2 228个单元;为便于对强降雨条件下粗粒土高路堤边坡渗流场的的监测,在边坡表面以下2 m处布设4个特征监测点~,在路堤左侧布设特征截面1-1。
渗流边界条件为:边坡表面和坡脚左侧均设置为降雨入渗边界,路堤表面及模型底部设定为不透水 边界。

图2 二维渗流计算模型
二维渗流计算参数如下:取工程边坡粗粒土试样,然后测定水文参数,其中,粗粒土饱和渗透系数经室内变水头渗透试验测量,为1.39×10−6 m/s,饱和体积含水率为0.28,残余体积含水率为0.11。然后,利用VAN GENUCHTEN模型[8]对边坡土水特征曲线及渗透系数方程进行拟合,拟合曲线如图3所示。此外,根据该边坡当地近50年降雨资料[18],拟定本文所采用的降雨等级为暴雨,降雨强度为12×10−7 m/s,降雨历时48 h,降雨停止48 h,总研究历时96 h。

1—粗粒土体积含水率;2—粗粒土渗透系数。
2.2 边坡在X方向的渗流梯度分布规律
图4和图5所示分别为降雨历时48 h和降雨停止48 h时边坡在方向的渗流梯度分布规律。从图4和图5可以看出:在降雨阶段,边坡在方向的渗流梯度在边坡表面及第2级边坡坡脚处表现为正值,并随着降雨历时增加,其正值所包围的区域也逐渐向边坡内部扩展;当降雨历时达到48 h时,边坡第2级坡脚处的渗流梯度已经延伸至模型底部,路堤中线附近在方向的渗流梯度为0;降雨停止48 h后,边坡在方向的渗流梯度在边坡表面出现了负值;在第2级边坡坡脚处,渗流梯度所包围的区域明显减小,并由模型底部向第2级边坡坡脚处抬升,路堤中线附近的方向的渗流梯度仍然表现为0。产生上述变化的原因为:在降雨阶段,雨水在路堤边坡表面主要表现为降雨入渗,入渗的雨水又由于自重应力场的作用而逐渐向第2级边坡坡脚处渗流,从而对坡脚处地下水进行补给,使得边坡在方向的渗流在第2级边坡坡脚处主要表现为正值,且随着降雨入渗对地下水的持续补给,其正值所包围的区域逐渐扩展;降雨停止后,边坡表面入渗的雨水逐渐向外渗透,第2级边坡坡脚处地下水位也将随之降低,因此,在降雨停止48 h后,边坡表面在方向的渗流梯度表现为负值。
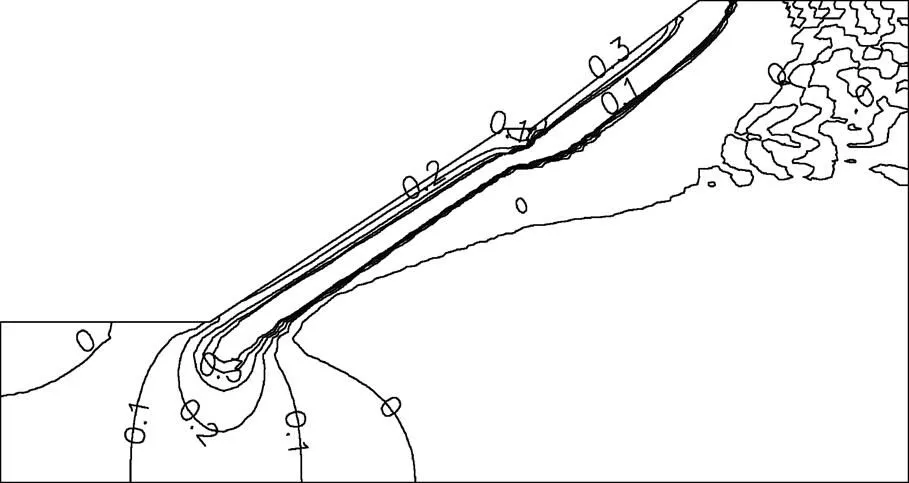
图4 降雨历时48 h边坡在X方向的渗流梯度
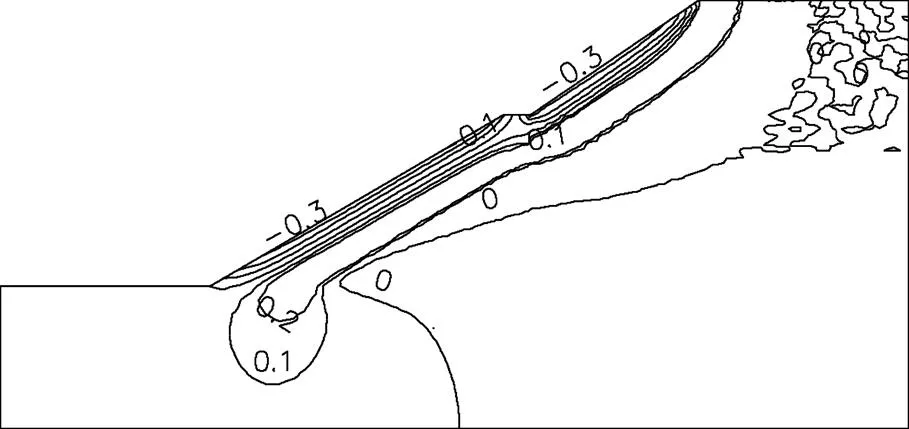
图5 降雨停止48 h在边坡X方向的渗流梯度
2.3 边坡特征点渗流梯度分布规律
图6所示为路堤边坡特征点在和方向的渗流梯度分布规律。从图6可知:在降雨初期,边坡特征监测点在方向的渗流梯度增大迅速,当降雨达到30 h左右时,达到峰值,然后开始持续降低,最后稳定在0左右;边坡特征点在方向的渗流梯度降雨初期主要沿轴负方向增加,随后又慢慢减小,最后稳定在−1左右;路堤边坡特征监测点在和方向的渗流梯度变化幅度最大,特征监测点次之。产生上述现象的原因为:在降雨初期,雨水会由于基质吸力及自重应力场的作用,产生沿轴正方向和轴负方向的合流,因此,边坡特征点在和方向的渗流梯度都会迅速增加,当特征点区域形成暂态饱和区后,其渗流速度矢量会明显减小,从而引起特征点在和方向的渗流梯度达到峰值后开始逐渐减小;降雨停止后,边坡表面雨水一部分会向外出渗,另一部分会继续向边坡内部渗流,因此,最后边坡特征点在和方向的渗流梯度都维持在最初值;特征监测点位于第2级边坡坡顶处,由于边坡平台的存在,此处的雨水渗流速度较大,因此,特征监测点的渗流梯度变化幅度最大。
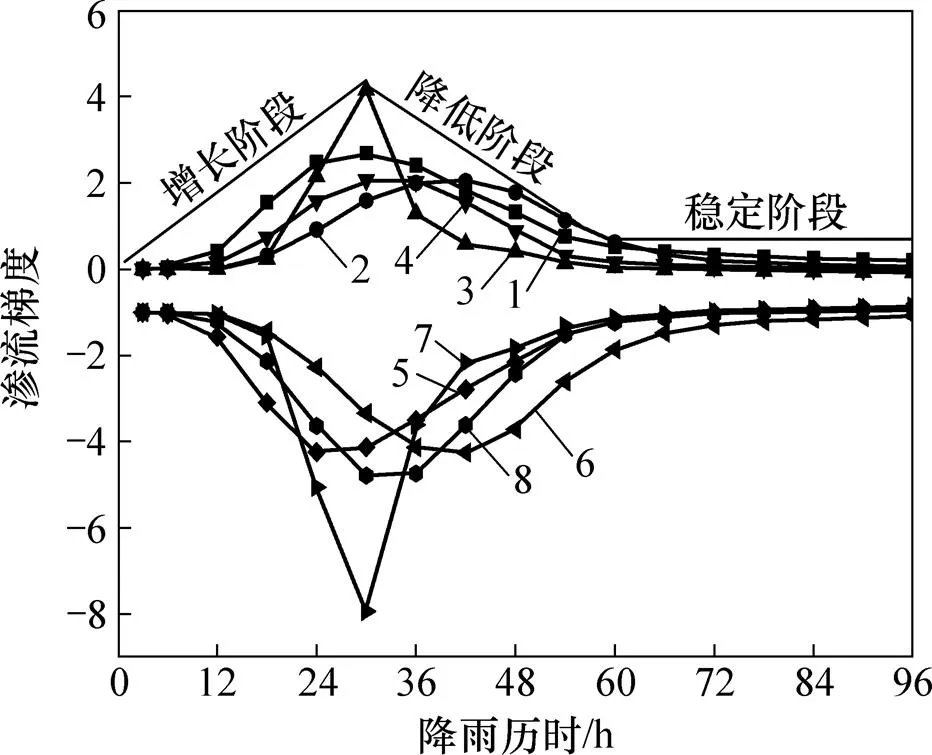
1—特征监测点a在X方向的渗流梯度;2—特征监测点b在X方向的渗流梯度;3—特征监测点c在X方向的渗流梯度;4—特征监测点d在X方向的渗流梯度;5—特征监测点a在Y方向的渗流梯度;6—特征监测点b在Y方向的渗流梯度;7—特征监测点c在Y方向的渗流梯度;8—特征监测点d在Y方向的渗流梯度。
2.4 边坡孔隙水压力及体积含水率分布规律
图7所示为路堤边坡特征点孔隙水压力分布规律,图8所示为路堤边坡截面1-1体积含水率分布规律。从图7可以看出:在降雨阶段,边坡特征点负孔隙水压力随着降雨历时的增加而逐渐减小,其中特征点的负孔隙水压力从−82 kPa逐渐减小至0 kPa,减小幅度最大;特征点负孔隙水压力在降雨历时48 h时减小至10 kPa,峰值最大;降雨停止后,边坡各特征点孔隙水压力逐渐恢复至负值。从图8可以看出:路堤边坡坡顶处体积含水率在降雨入渗条件下迅速增加至饱和状态,形成暂态饱和区;降雨停止后,坡顶
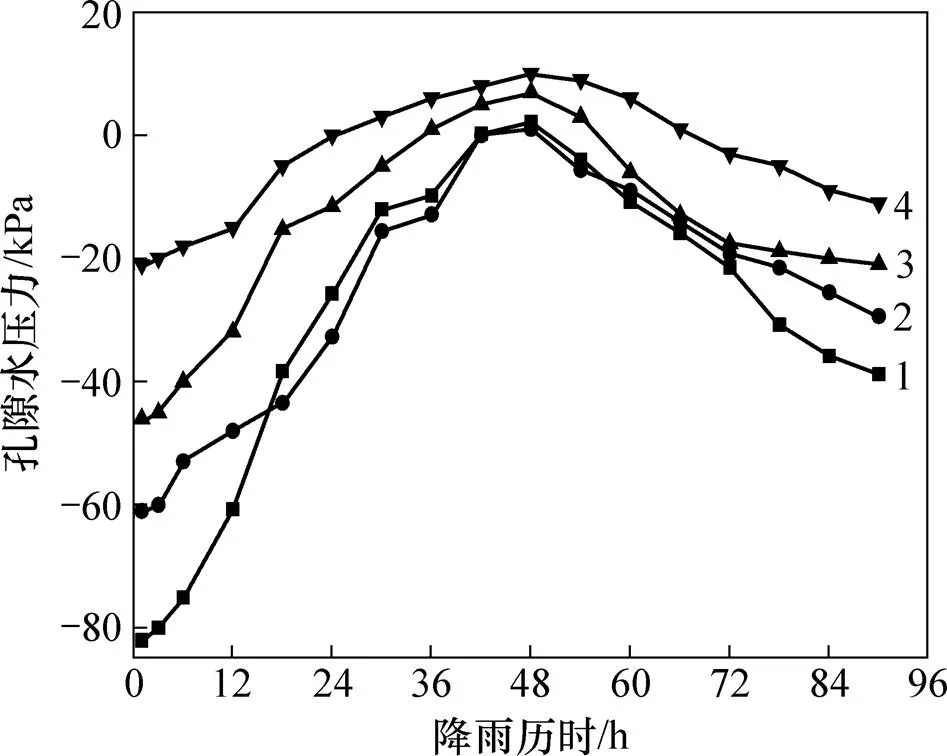
特征监测点:1—a;2—b;3—c;4—d。

图8 路堤边坡截面1-1体积含水率
3 边坡稳定性研究
3.1 计算模型及参数
通过FLAC3D软件建立粗粒土高路堤边坡的稳定性计算模型,其横截面尺寸、网格划分和单元个数与2.1节中建立的渗流模型一致(见图9);然后,将渗流计算结果中的孔隙水压力及渗透力等渗流特性参数按节点的方式通过Fish语言导入到FLAC3D软件中,计算粗粒土高路堤边坡的稳定性。本文只给出降雨历时为48 h时导入孔隙水压力及渗透力等渗流特性的稳定性计算模型,如图10所示。

图9 稳定性计算模型
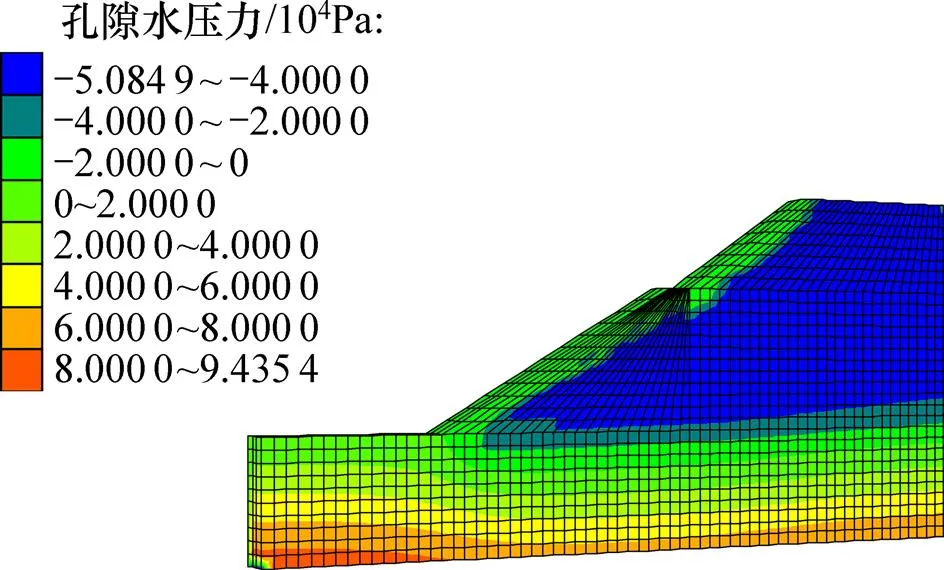
图10 导入渗流特性的稳定性计算模型
按照JTG E40—2007“公路土工试验规程”对该边坡粗粒土试样进行室内大型直剪试验,测得其黏聚力为36 kPa,内摩擦角为26°,天然重度为18 kN/ m3。此外,其他物理力学参数参照文献[19−21]进行取值,如表1所示。

表1 物理力学参数
3.2 边坡塑性区发育规律
边坡的失稳破坏可以看作是塑性区逐渐形成、扩展直至贯通,继而形成完全的塑流状态,导致边坡无法继续承受荷载的过程。图11所示为数值分析得到的强降雨条件下路堤边坡塑性区发育规律。从图11可以看出:在降雨初期阶段,路堤边坡塑性区首先在各级边坡坡脚处及第2级边坡坡脚下方形成,然后,随着降雨历时增加,塑性区面积不断增大,并逐渐沿坡顶方向向边坡内部扩展;当降雨历时达到48 h时,塑性区已经由边坡表面扩展至边坡内部,形成塑性贯通区;当降雨停止后,路堤边坡塑性区面积由中间向两边逐渐缩减;当降雨停止48 h后,路堤边坡边坡塑性贯通区已经消散,此时,塑性区主要分布在模型边界处。其原因为:在降雨初期阶段,路堤边坡坡脚处的渗流梯度较大,渗透力较强,雨水主要沿坡脚向下渗流,使得边坡坡脚处孔隙水压力逐渐增大,地下水位逐渐沿坡脚爬升,粗粒土抗剪强度逐渐降低,因此,路堤边坡塑性区首先在各级边坡坡脚处及第2级边坡坡脚下方形成;随着降雨历时增加,雨水不断向边坡内部渗流,边坡坡顶及边坡内部的渗透力逐渐增加,孔隙水压力逐渐增大,从而引起边坡塑性区逐渐沿坡顶方向向边坡内部扩展;当降雨停止后,雨水在边坡表面出渗,边坡表面渗流梯度开始逐渐减小至负值,孔隙水压力也开始慢慢恢复,因此,路堤边坡塑性区面积又逐渐缩减,贯通现象逐渐消失。

(a) 降雨历时12 h塑性区;(b) 降雨历时48 h塑性区;(c) 降雨停止48 h塑性区
3.3 边坡安全系数演变规律
路堤边坡稳定性安全系数[22]是指边坡刚好处于临界失稳状态时,对边坡结构层岩土体的抗剪强度进行折减的程度,反映了边坡整体结构的稳定性:在降雨条件下,当其小于1.0时,边坡处于失稳状态;当其为[1.0,1.35)时,边坡处于欠稳定状态;当其大于等于1.35时,边坡处于稳定状态。本文运用强度折减法,对粗粒土高路堤边坡的安全系数进行计算,其演变规律如图12所示。从图12可以看出在整个研究历时中,路堤边坡安全系数的演变规律分为4个阶段:在0~12 h内,边坡安全系数从1.80上升至1.65,平均每小时上升0.004,为缓慢上升阶段;在12~24 h内,边坡安全系数从1.85下降至1.73,平均每小时下降0.010,为缓慢下降阶段;在24~48 h内,边坡安全系数从1.73下降至1.10,平均每小时下降0.026,为快速下降阶段;在48~96 h内,边坡安全系数从1.10回升至1.45,平均每小时回升0.007,为缓慢回升阶段。在降雨历时48 h内,边坡安全系数从1.80下降至1.10,降低了43.8%;降雨停止48 h后,边坡安全系数从1.10回升至1.45,回升了38.9%。产生上述演变规律的原因为:在降雨前期,只有少量雨水在边坡表面入渗,雨水填充边坡表面粗粒土骨架孔隙,在边坡表面形成沿轴正方向和轴负方向的渗透力,从而边坡的稳定性有所提高;但随着雨水持续入渗,边坡表面孔隙水压力逐渐增大,粗粒土抗剪强度慢慢降低,边坡稳定性又开始缓慢降低;当降雨量达到一定程度后,边坡表面逐渐形成暂态饱和区,塑性区面积逐渐沿坡顶方向向边坡内部扩展,因此,边坡稳定性开始迅速降低;当降雨停止后,随着雨水在缓慢出渗,边坡塑性区贯通现象慢慢消散,暂态饱和区面积开始缩减,孔隙水压力逐渐恢复,因此,边坡稳定性缓慢提高。
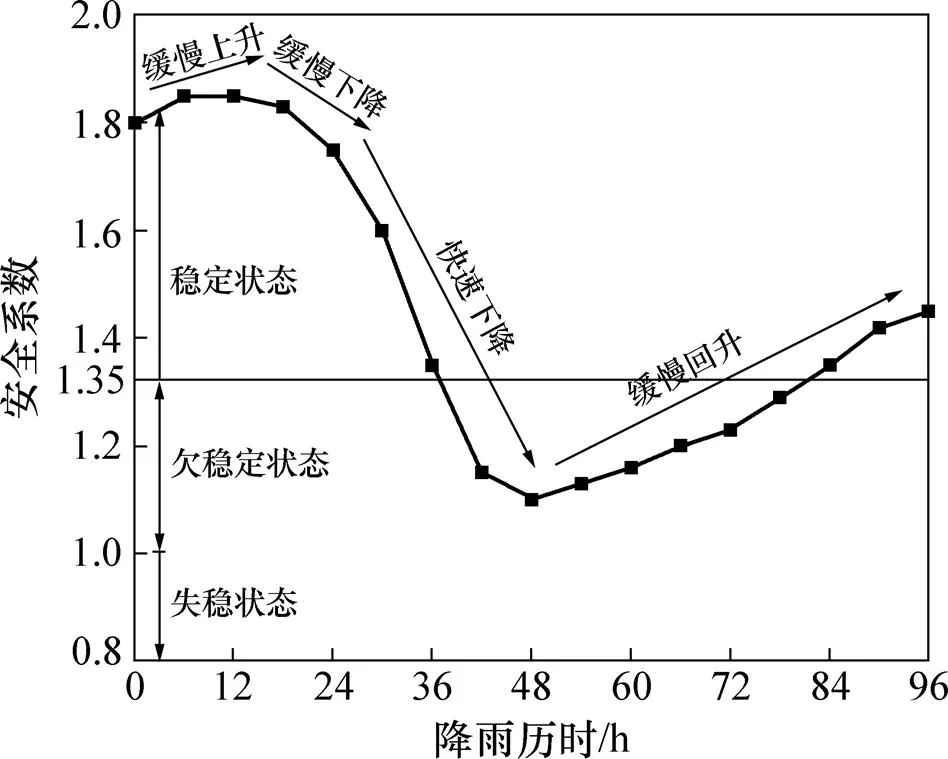
图12 路堤边坡安全系数演变规律
4 结论
1) 在降雨阶段,边坡在方向的渗流梯度在边坡表面及第2级边坡坡脚处表现为正值,并随着降雨历时增加,坡脚处包络线所包围的正值区域逐渐向边坡内部扩展;边坡坡顶处在和方向的渗流梯度的变化幅度较大。
2) 路堤边坡表层孔隙水压力随降雨入渗的持续而逐渐增加,随雨水的不断渗透而逐渐减小;在整个研究历时内,路堤边坡坡顶处体积含水率呈现“凸”型分布,边坡纵截面体积含水率呈现“凹”型分布。
3) 在强降雨条件下,受渗透力影响,路堤边坡塑性区首先在各级边坡坡脚处及第2级边坡坡脚下方形成,并逐渐沿坡顶方向向边坡内部扩展,形成塑性贯通区;在渗透力影响下,边坡安全系数演变规律分为缓慢上升阶段、缓慢下降阶段、快速下降阶段和缓慢回升阶段。
[1] 刘俊新, 刘育田, 胡启军. 非饱和地表径流−渗流和流固体耦合条件下降雨入渗对路堤边坡稳定性研究[J]. 岩土力学, 2010, 31(3): 903−910. LIU Junxin, LIU Yutian, HU Qijun. Stability of embankment slope subjected to rainfall infiltration considering both runoff-underground seepage and fluid-solid coupling[J]. Rock and Soil Mechanics, 2010, 31(3): 903−910.
[2] 徐平, 李同录, 李萍. 考虑非饱和渗流作用下三峡库岸滑坡稳定性研究[J]. 中国地质灾害与防治学报, 2010, 21(1): 7−12. XU Ping, LI Tonglu, LI Ping. Study on the stability of the Three Gorges reservoir slope under the consideration of unsaturated seepage[J]. The Chinese Journal of Geological Hazard and Control, 2010, 21(1): 7−12.
[3] MEIN R G, LARSON C L. Modeling Infiltration on during a steady rain[J]. Water Resources Research, l973, 9(2): 384−394.
[4] DUNKERLEY D. An approach to analysing plot scale infiltration and runoff responses to rainfall of fluctuating intensity[J]. Hydrol Process, 2017, 31(1): 191−206.
[5] 张卢明, 郑明新, 何敏. 滑坡防治前后滑带土基质吸力特征研究[J]. 岩土力学, 2010, 31(10): 3305−3312. ZHANG Luming, ZHENG Mingxin, HE Min. Study of characteristics of matric suction in landslide slip soils before and after landslide control[J]. Rock and Soil Mechanics, 2010, 31(10): 3305−3312.
[6] 毛昶熙. 渗流计算分析与控制[M]. 北京: 中国水利水电出版社, 2003: 56−63. MAO Changxi. Seepage computation analysis & control[M]. Beijing: China Water Power Press, 2003: 56−63.
[7] FREDLUND D G, MORGENSTERN N R, WILDGER R A. The shear strength of unsaturated soils[J]. Can Geotech J, 1978, 15(3): 313−321.
[8] RAHARDJO H, ONG T H, REZAUR R B. Factors controlling instability of homogeneous soil slopes under rainfall[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(12): 1532−1543.
[9] 蒋中明, 龙芳, 熊小虎, 等. 边坡稳定性分析中的渗透力计算方法考证[J]. 岩土力学, 2015, 36(9): 2478−2486. JIANG Zhongming, LONG Fang, XIONG Xiaohu, et al. Study of calculation methods of acting force of seepage in slope stability analysis[J]. Rock and Soil Mechanics, 2015, 36(9): 2478−2486.
[10] 何忠明, 邓喜, 付宏渊, 等. 降雨工况下渗透力对粗粒土高路堤边坡稳定性的影响[J]. 公路交通科技, 2017, 34(9): 14−21. HE Zhongming, DENG Xi, FU Hongyuan, et al. Influence of seepage force on stability of coarse grained soil high embankment under rainfall condition[J]. Journal of Highway and Transportation Research and Development, 2017, 34(9): 14−21.
[11] 邹金锋, 李帅帅, 张勇, 等. 考虑轴向力和渗透力时软化围岩隧道解析[J]. 力学学报, 2014, 46(5): 747−755. ZOU Jinfeng, LI Shuaishuai, ZAHNG Yong, et al. Analysis of tunnel analysis of softened surrounding rock considering axial force and permeability[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(5): 747−755.
[12] 丁洲祥. 渗透力概念的力学分析及广义化探讨[J]. 岩土工程学报, 2017, 39(11): 2088−2101. DING Zhouxiang. Mechanical fundamentals of seepage force concept and its generalization[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(11): 2088−2101.
[13] 李广信. 论土骨架与渗透力[J]. 岩土工程学报, 2016, 38(8): 1522−1528. LI Guangxin. On soil skeleton and seepage force[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(8): 1522−1528.
[14] 郑颖人, 时卫民, 孔位学. 库水位下降时渗透力及地下水浸润线的计算[J]. 岩石力学与工程学报, 2004, 23(18): 3203−3210. ZHENG Yingren, SHI Weimin, KONG Weixue. Calculation of seepage force and groundwater infiltration line when reservoir water level falls[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(18): 3203−3210.
[15] 李镜培, 梁发云, 赵春风. 土力学[M]. 北京: 高等教育出版社, 2008: 126−127. LI Jingpei, LIANG Fayun, ZHAO Chunfeng. Soil mechanics[M]. Beijing: Higher Education Press, 2008: 126−127.
[16] 曾铃, 付宏渊, 何忠明, 等. 饱和-非饱和渗流条件下降雨对粗粒土路堤边坡稳定性的影响[J]. 中南大学学报(自然科学版), 2014, 45(10): 3614−3620. ZENG Ling, FU Hongyuan, HE Zhongming, et al. Impact of rainfall on stability of granular soil embankment slope considering saturated-unsaturated seepage[J]. Journal of Central South University (Science and Technology), 2014, 45(10): 3614−3620.
[17] 蒋泽锋, 朱大勇, 沈银斌, 等. 非饱和−非稳定渗流条件下的边坡临界滑动场[J]. 岩土力学, 2015, 36(6): 1815−1823. JIANG Zefeng, ZHU Dayong, SHEN Yinbin, et al. Critical slip field of slope under the condition of transient unsaturated seepage[J]. Rock and Soil Mechanics, 2015, 36(6): 1815−1823.
[18] 李湘龙, 张坤. 长沙市近50年降水特征及变化趋势[J]. 农村经济与科技, 2015, 26(9): 44−46. LI Xianglong, ZHANG Kun. Precipitation characteristics and change trend in recent 50 years in Changsha[J]. Rural Economy and Science-Technology, 2015, 26(9): 44−46.
[19] 王保林, 何忠明, 胡庆国, 等. 降雨工况下不同软弱夹层出露面对黏性土坡稳定性影响分析[J]. 中外公路, 2017, 37(6): 15−19. WANG Baolin, HE Zhongming, HU Qingguo, et al. Analysis of the influence of different soft interlayer exposure on the stability of viscous soil slope under rainfall conditions[J]. Journal of China & Foreign Highway, 2017, 37(6): 15−19.
[20] 汪丁建, 唐辉明, 张雅慧, 等. 粗粒土试验与力学特性研究现状[J]. 冰川冻土, 2016, 38(4): 943−954. WANG Dingjian, TANG Huiming, ZHANG Yahui, et al. Present situation of research on test and mechanical properties of coarse-grained soil[J]. Journal of Glaciology and Geocryology, 2016, 38(4): 943−954.
[21] 何忠明, 邓喜, 唐昊龙, 等. 降雨工况下粗粒土高路堤边坡暂态饱和区时空演变规律模型试验[J]. 中国公路学报, 2018, 31(2): 261−269. HE Zhongming, DENG Xi, TANG Haolong, et al. Experiment on spatial and temporal evolution of transient saturated zone of coarse soil high embankment slope under rainfall condition[J]. China Journal of Highway and Transport, 2018, 31(2): 261−269.
[22] 陈国庆, 黄润秋, 石豫川, 等. 基于动态和整体强度折减法的边坡稳定性分析[J]. 岩石力学与工程学报, 2014, 33(2): 243−256. CHEN Guoqing, HUANG Ruiqiu, SHI Yuchaun, et al. Stability analysis of slope based on dynamic and whole strength reduction methods[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 243−256.
(编辑 陈灿华)
Stability of coarse grained soil with high embankment considering permeability under strong rainfall condition
DUAN Xulong1, HE Zhongming2, WANG Baolin2
(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China; 2. School of Traffic and Transportation Engineering, Changsha University of Science & Technology, Changsha 410114, China)
In order to analyze the stability of coarse grained soil with high embankment under strong rainfall condition, two-dimensional seepage characteristics of slope under heavy rainfall conditions were calculated based on the penetration theory. The seepage pore water pressure and seepage force were imported into FLAC3D software by Fish language programming. The impact of the change of seepage force on the stability of embankment slope was analyzed. The results show that under strong rainfall conditions, the seepage gradient of embankment slope indirection is positive on the surface of the slope and at the foot of the second grade slope. The positive area surrounded by the envelope of the slope foot gradually extends to the interior of the slope, and the rate of change of the seepage gradient inanddirections at the top of the slope is larger. The pore water pressure on the surface of the embankment slope increases gradually with the infiltration of the continuous rainfall, and gradually decreases with the continuous exudation of the rain water. The volumetric water content of embankment slope top shows “convex” distribution, and the vertical section of the slope shows “concave” distribution. With the continuous infiltration of rainwater, the plastic zone of embankment slope is firstly formed at the foot of slope and at the foot of the second grade slope, and gradually extends to the interior of the slope along the top of the slope to form a plastic penetrating zone. Influenced by the seepage force, the evolution law of slope safety factor is divided into 4 stages, i.e. slow rising stage, slow decline stage, rapid descent stage and slow recovery stage.
strong rainfall; coarse grained soil; stability; seepage force; safety factor
10.11817/j.issn.1672−7207.2018.08.023
U416.12
A
1672−7207(2018)08−2016−08
2017−10−14;
2017−12−22
国家自然科学基金资助项目(51508042,51678073)(Projects(51508042, 51678073) supported by the National Natural Science Foundation of China)
何忠明,博士(后),教授,从事道路工程研究;E-mail:hezhongming45@126.com
