考虑冻融作用的混凝土单轴压缩损伤本构模型
2018-09-07龙广成刘赫马昆林谢友均
龙广成,刘赫,马昆林,谢友均
考虑冻融作用的混凝土单轴压缩损伤本构模型
龙广成,刘赫,马昆林,谢友均
(中南大学 土木工程学院,湖南 长沙,410075)
为研究冻融循环作用后混凝土的应力−应变行为及其在冻融作用后的持荷性能,对比研究同为C40强度等级的普通混凝土(NC)与自密实混凝土(SCC)经受冻融作用后的单轴压缩应力−应变关系,并进一步基于应变等价性假说和统计损伤理论建立冻融循环作用后混凝土单轴压缩损伤本构模型,探讨相应损伤变量随冻融循环作用次数和单轴压缩应变发展的演变特性。研究结果表明:所建立的损伤本构模型可较好地描述冻融循环作用后NC和SCC在单轴压缩荷载下的应力−应变关系;在单轴压缩过程中,冻融循环产生的微裂纹闭合导致损伤变量增长速率下降;NC与SCC的冻融损伤变量随冻融次数变化的规律均可用指数函数进行预测;掺入膨胀剂和黏度改性材料可以有效降低SCC的冻融损伤速率。
冻融循环;应力−应变曲线;单轴压缩损伤本构模型;自密实混凝土
冻融循环作用是影响混凝土耐久性的重要因素之一,为此,人们对混凝土的抗冻性能进行了大量研究,同时,针对冻融作用下混凝土的损伤演变规律也开展了不少研究工作。商怀帅等[1]基于疲劳累积损伤的冻融可靠度分析模型对混凝土冻融损伤特性进行分析;杜鹏等[2]则使用残余应变来表征由冻融引起的混凝土内部损伤程度;田威等[3]采用强度损伤系数来描述混凝土冻融损伤随冻融次数的变化规律;冀晓东等[4]结合OTTOSEN理论和有限元方法来研究混凝土的冻融损伤本构模型;关宇刚等[5−6]结合可靠度及损伤理论,提出不同作用条件下的混凝土寿命预测模型,并讨论了冻融条件混凝土寿命预测的有效性[6];DUAN等[7]采用随机损伤变量对混凝土冻融损伤进行了研究;PENTTALA[8]通过线性回归方法得到冻融循环作用下混凝土损伤变量与水灰比、含气体积及养护时间等变量的影响关系;YU等[9]采用动态弹性模量参数来表征冻融作用下混凝土性能的衰变。以上这些研究大都是针对冻融作用本身对混凝土损伤规律的影响,虽然人们对冻融循环作用后混凝土的力学性能变化进行了较深入的研究[10−14][11][12][13][14],但对有关冻融循环作用后NC和SCC受荷载作用下损伤发展规律及其应力−应变本构模型研究较少,而对有关掺膨胀剂、黏度改性剂等胶凝材料组成的SCC的相关研究更少。为此,本文作者针对冻融循环作用后NC和SCC的应力应变关系,结合试验和理论分析,建立考虑冻融循环作用的损伤本构模型,研究冻融后混凝土的力学行为及其损伤演化规律,确保严寒环境下的混凝土结构能够安全服役。
1 试验简介
1.1 原材料
水泥(C)为湘江水泥厂生产的P.O42.5,28 d实测抗压强度为48.6 MPa;粉煤灰(FA)产自于湘潭电厂,比表面积为460 m2/kg,密度为2.36 g/cm3;矿渣(GGBS)产自于上海宝钢新材料公司;膨胀剂采用唐山北极熊建材公司生产的UEA膨胀剂(UEA);黏度改性剂(VEA)由无机活性含钙、硅的矿质超细粉体及聚合物组成,高效减水剂(SP)为聚羧酸类减水剂,其减水率为30%(质量分数),含固量为33%(质量分数);拌合用水(W)为自来水。水泥、粉煤灰、矿渣的物理性质及化学组成如表1所示。细骨料采用普通河砂(S),其表观密度为2.65 g/cm3,细度模数为2.62,级配满足中砂级配要求;粗骨料(G)是由粒径分别为5~10 mm和10~20 mm的2种级配的石灰石碎石混合而成,表观密度为2.70 g/cm3。
1.2 配合比及试验方法
为便于对比,设计强度等级同为C40的3组SCC及1组NC这2个系列试件,各试验混凝土配合比如表2所示。由表2可知:3组SCC的粗、细骨料用量相同,总体积分数为615 L/m3,主要改变了胶凝材料组成。NC组中FA和GGBS占总胶凝材料的质量分数与SCC1的相同,分别为15%和20%,骨料总体积分数为660 L/m3。按照上述配合比,采用60 L容量强制式搅拌机进行混合料拌合,对搅拌均匀的拌合物首先测试其工作性,然后分别制成长×宽×高为100 mm× 100 mm×100 mm立方体及100 mm×100 mm× 300 mm棱柱体试件,1 d后拆模,置于(20±2) ℃和相对湿度大于95%的养护室中进行养护。至56 d龄期时参照GB/T 50081—2002“普通混凝土力学性能试验方法标准”进行混凝土立方体抗压强度测试。采用长×宽×高为100 mm×100 mm×300 mm棱柱体试件并参照GB/T 50082—2009“普通混凝土长期性能和耐久性能试验方法标准”中的快冻法进行冻融试验及相应应力应变曲线测试。各试样工作性能及立方体抗压强度结果如表3所示(其中50为SCC从坍落度开始至扩展度达到50 cm时所用的时间)。

表1 水泥、粉煤灰及矿渣的物理性质与化学组成(质量分数)

表2 各试验混凝土配合比

表3 混凝土拌合物工作性能及56 d龄期混凝土立方体抗压强度
2 应力−应变曲线试验结果
经受不同冻融循环次数作用后,NC组与3个SCC组试样的应力−应变全曲线测试结果如图1所示,图例中NC和SCC表示混凝土类型,后面数字表示经受的冻融作用次数,如NC-100表示普通混凝土经受100次冻融循环作用,依此类推。由图1可知:经冻融作用后,各试样的应力应变曲线出现明显变化;随着冻融循环次数增加,试样应力−应变曲线呈现偏离轴方向趋势,峰值应力显著降低,峰值应变逐渐增加。进一步对图1中各试样的应力−应变曲线特征指标进行分析,结果如表4所示(其中,cp为峰值强度;f为峰值应变;为弹性模量,采用=0.3cp时的割线模量作为混凝土的静态弹性模量)。由表4可知:经受冻融循环300次后,NC及SCC1~SCC3试样的峰值应力分别下降34.0%,31.3%,28.6%及22.2%,相应峰值应变增加98.5%,47.2%,35.8%及35.2%,相应弹性模量分别下降52.0%,39.6%,37.6%及33.1%。这表明,经受冻融循环后,同强度等级的NC比SCC的应力应变衰减更为显著。

(a) NC;(b) SCC1;(c) SCC2;(d) SCC3

表4 不同冻融循环作用下各混凝土应力−应变曲线特征指标
3 考虑冻融循环作用的损伤本构 模型
3.1 模型建立
由LEMAITRE应变等价性假说[15]可知:全应力作用在损伤材料上产生的应变与有效应力作用在无损材料上引起的应变等价。因此,在冻融循环作用下混凝土的损伤本构关系可用下式表示:
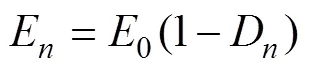
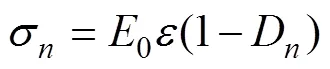
式中:σ为冻融次后的应力;0为混凝土初始静态弹性模量;D为冻融次后的损伤变量;为应变;E为冻融次后的混凝土静态弹性模量。
将混凝土冻融损伤作为第1阶段损伤状态,将冻融后的混凝土所受荷载作用作为第2阶段损伤状态,由应变等价原理可知冻融后的混凝土在荷载作用下的损伤本构关系为
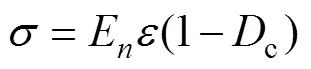
式中:c为荷载作用引起的损伤变量。
将式(1)代入式(3),可得冻融后混凝土在荷载作用下的本构关系为
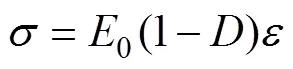
式中:为混凝土冻融循环受荷后的总损伤变量,cc。
根据宏观唯象损伤力学,混凝土宏观物理力学性能的响应能够表征内部的劣化程度[16],则混凝土冻融循环次后的损伤变量为

宏观上,混凝土可视作由无数细小微元组成的整体,每一个微元的力学性能直接影响混凝土的整体性能。当混凝土承受荷载时,其损伤程度与各细小微元有关,假设微元强度分布符合WEIBULL概率分布,则其概率密度函数()为[17]
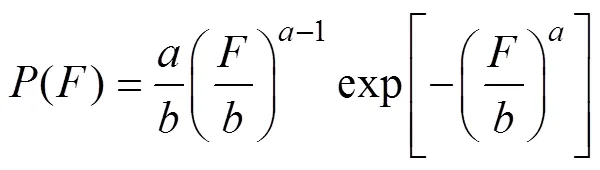
式中:为微元强度分布的分布变量;和分别为WEIBULL分布参数。
在一定单轴压缩应变条件下,混凝土中微元破坏的数目d与总微元数t可表示为
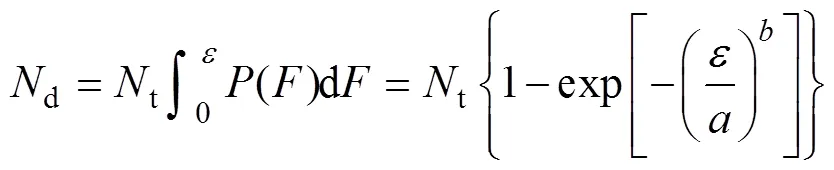
则荷载作用下的损伤变量c可用破坏微元与总微元的比值表示:
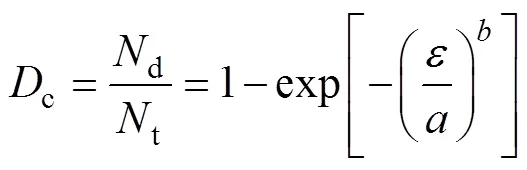
因此,冻融循环后混凝土在荷载作用下的总损伤变量可用式(9)表示如下:
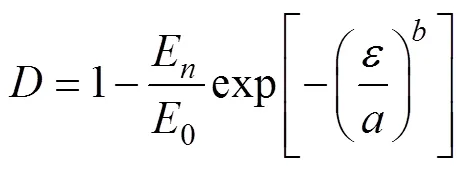
将式(9)代入式(4)可得到经冻融循环作用次后混凝土受荷本构关系:
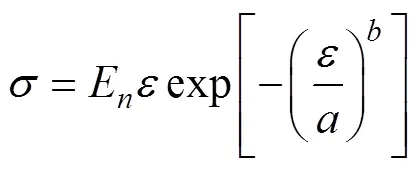
3.2 模型参数的物理意义
图2所示为在保持E和不变时,参数对试样应力−应变曲线的影响,以及保持E和不变时,参数对相应应力−应变曲线的影响。
由图2(a)可知:随着参数不断增大,相应应力−应变曲线形状基本无明显变化,但应力−应变曲线峰值应力、峰值应变均不断增大。由图2(b)可知:随着参数不断增大,相应应力−应变曲线上升段中弹性变形所占比例不断增加,而曲线下降段越陡,破坏速度加快,脆性有所提高。由此可知:模型参数可反映峰值应变,越大,表明相应的峰值应变越大;而参数则反映试样的脆性特征,越大,表明其脆性越大,极限应变小。
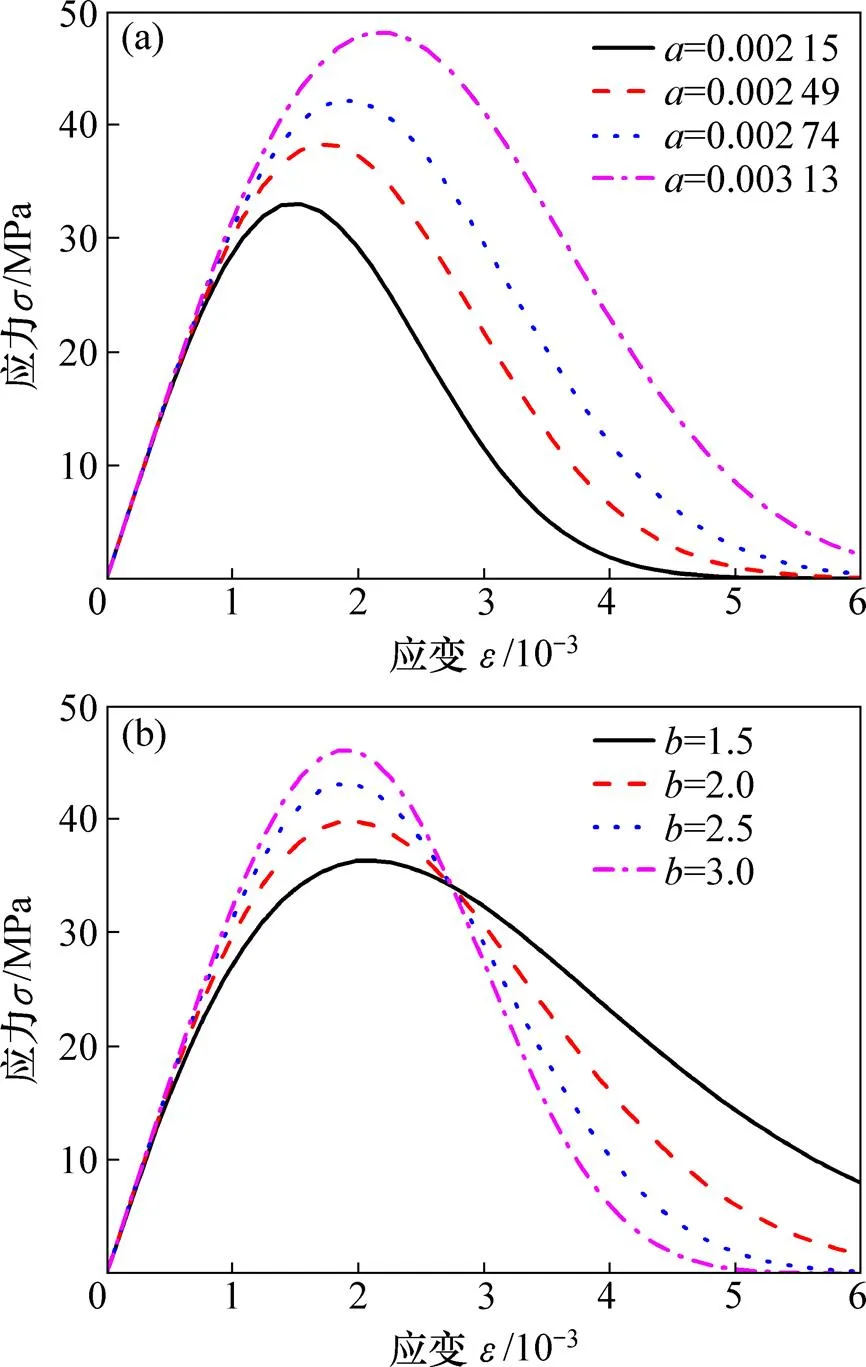
(a) 参数a不同时的应力−应变曲线;(b) 参数b不同时的应力−应变曲线
3.3 模型参数计算及验证
对式(10)两边取对数可得:
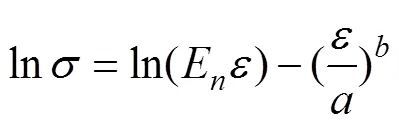
将式(11)两边取对数可得
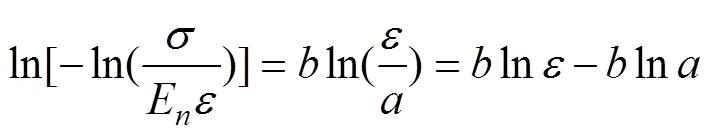
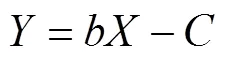
式中=ln,通过数据变换和线性拟合可得到和的关系式:

计算得到的本构模型相关参数如表5所示。模型计算得到的应力−应变曲线结果与试验结果对比如图3所示。
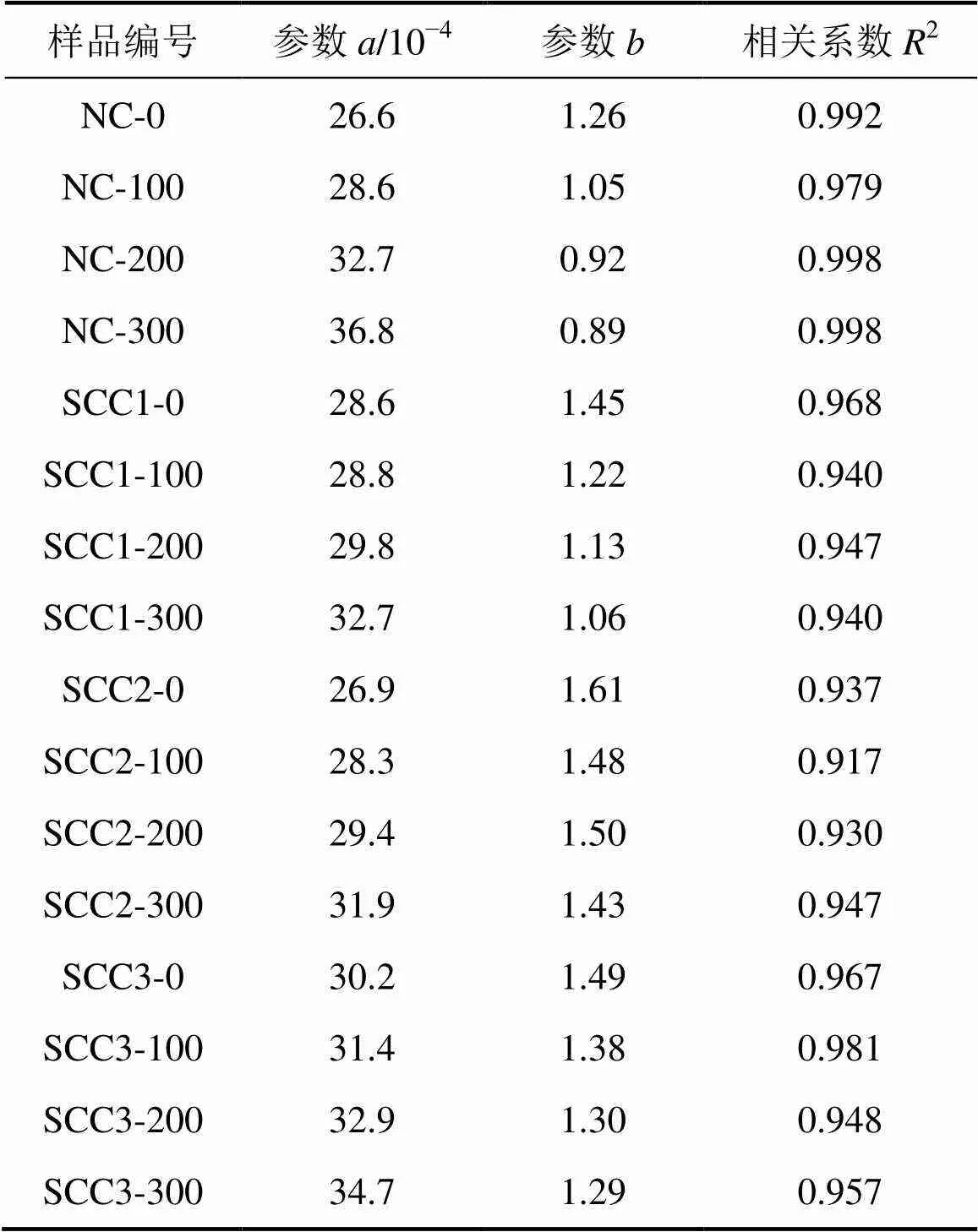
表5 本构模型相关参数
由表5可知:冻融循环300次后,NC和SCC1,SCC2和SCC3模型参数分别增加38.3%,14.3%,18.6%和17.5%,说明在冻融循环作用下NC峰值应变增加最为明显,其次为SCC2和SCC3,最后为SCC1,这与本文试验结果规律一致;而模型参数分别降低29.3%,26.9%,11.2%和13.4%。由此可以看出:在冻融循环作用下,NC峰值应变和极限应变大幅提高,其次为SCC1,SCC2与SCC3则变化不明显,这与图1中应力−应变形状变化规律一致,且冻融循环作用下混凝土的脆性特征减弱。由表5及图3可知:本构模型拟合结果与试验结果的相关系数均在0.91以上,且峰后应力−应变曲线相关性较好,说明本文所建立的本构模型能够对NC及SCC冻融循环后受荷的应力−应变关系进行准确预测。

样品:(a) NC;(b) SCC1;(c) SCC2;(d) SCC3
3.4 损伤变量演化特性
材料内部损伤不断累积是导致材料强度降低的主要原因。为进一步揭示不同冻融循环次数作用后混凝土力学损伤机制,根据式(9)对冻融循环后混凝土受荷作用的损伤变量进行计算。4组试样在不同冻融循环次数下损伤变量随应变的变化关系如图4所示。从图4可以看出:在各冻融循环次数下损伤变量随应变呈“S”型单调递增;当各试样应变达到4×10−3时,各自损伤变量基本都超过0.8,且随着应变和冻融循环次数增加,损伤变量的增长速率不断下降;同时,随着冻融次数增加,应变为0时所对应的初始损伤值不断增加。另外, 4组试样的损伤变量随应变、冻融次数的变化趋势相似,但NC在峰值应变后其损伤变量的发展速率比SCC的低。分析其原因,NC试样中骨料体积较大,导致混凝土中的浆骨界面数量大,C40混凝土裂纹扩展主要沿骨料与浆体界面扩展,从能量角度分析,裂纹在NC中扩展能够消耗更多的能量,同时NC中碎块间的摩阻力和机械咬合力均比SCC的大,导致NC峰后损伤变量发展速率比SCC的小,且极限应变较大。随着冻融次数增加,混凝土内部产生的微裂纹不断增多,孔隙不断增大,冻融损伤越严重,应变为0时对应的初始损伤值增大,使得同一应变对应的损伤变量不断增大。单轴压缩作用会使得冻融损伤产生的微裂纹出现闭合现象,消耗一部分能量,从而使损伤变量发展速率随着冻融次数增加而不断下降。因此,本文提出的本构模型中损伤变量能够准确描述冻融条件下的混凝土力学损伤演变 规律。
当应变为0时(见图4),4组试样冻融损伤变量随冻融作用次数的变化结果如图5所示。从图5可见:随着冻融次数增加,4组试样冻融损伤变量不断增加;冻融循环作用300次后,NC及SCC1,SCC2和SCC3损伤变量分别为0.52,0.40,0.38和0.32,表明SCC抗冻性能优于NC抗冻性能;相比于SCC1组试样,掺入UEA能够提高SCC2抗冻性能,同时掺入UEA和VEA对SCC抗冻性能有进一步提升作用。

样品:(a) NC;(b) SCC1;(c) SCC2;(d) SCC3 冻融循环数/次:1—0;2—100;3—200;4—300。
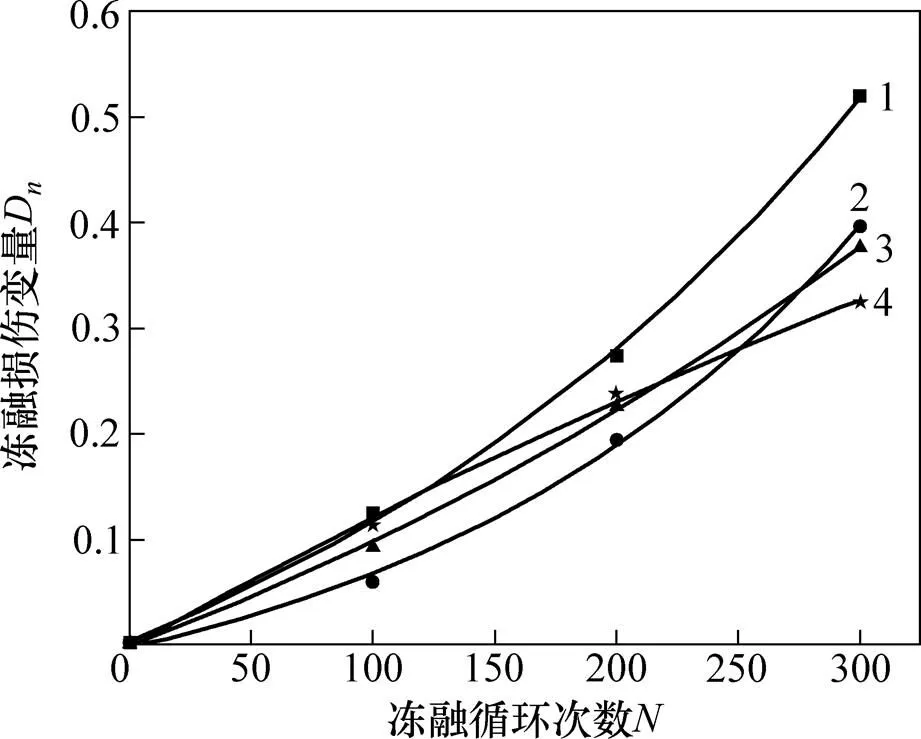
样品:1—NC;2—SCC1;3—SCC2;4—SCC3。
混凝土冻融损伤变量与冻融作用次数之间符合指数函数关系,对图5数据进行拟合,分别得到NC及SCC冻融损伤变量与冻融循环次数之间的经验关系式(其相关系数分别为0.998,0.996,0.998和0.984)。
NC:
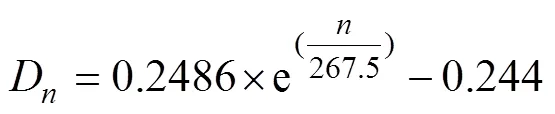
SCC1:
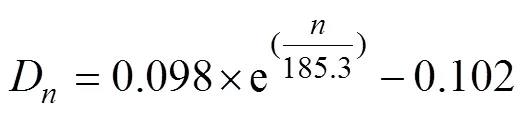
SCC2:
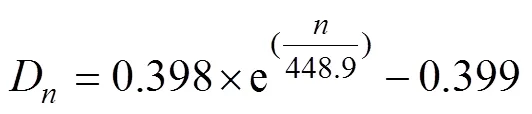
SCC3:
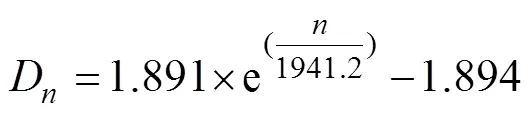
根据NC和SCC的与的关系式,对求导得到增长速率随冻融次数的变化规律,其结果如图6所示。由图6可知:NC试样的增长速率随冻融次数增加而发展最为迅速,且均比SCC试样的高。相比于基准试样SCC1,掺入UEA的SCC2试样的增长速率有所降低,而同时掺入UEA和VEA的SCC3的增长速率进一步降低。分析其原因,相比于NC,SCC浆体体积较大,骨料体积分数减小,浆体与骨料之间的界面过渡区数量降低,且SCC界面强度比NC的高[18],对于冻融作用产生的破坏应力有较好的抵抗作用,使得SCC在冻融作用下的损伤程度较小,从而其增长速率有所降低。相比于基准组SCC1,SCC2掺入UEA水化形成较多的膨胀性产物即钙矾石填充水泥石中的孔隙,使得总孔隙率减小,水泥石结构更加紧密[19],导致发展速率得到抑制。在SCC3中同时掺入UEA及VEA,VEA中的超细活性颗粒不仅能发挥良好的物理填充效应,而且能参与水化反应生成凝胶产物,改善水化物相,与UEA水化产物共同作用,使体系微结构进一步得到优化,最终导致发展速率较低。

样品:1—NC;2—SCC1;3—SCC2;4—SCC3。
4 结论
1) 所建立的考虑冻融作用的混凝土单轴压缩本构模型能够较好地描述冻融循环作用后NC和SCC的应力−应变关系,其中模型参数主要与峰值应变有关,参数主要决定应力−应变曲线下降段的形状,反映混凝土的脆性。
2) 冻融循环作用后的混凝土在单轴压缩荷载下的总损失变量随应变呈现“S”型单调增加趋势,且随着冻融循环作用次数增多其增加速率降低;相比于NC,SCC的总损伤变量增长曲线更为平缓。单轴压缩作用可使冻融损伤产生的微裂纹出现闭合而导致损伤变量增长速率有所下降。
3) 随着冻融循环作用次数增加,混凝土冻融损伤变量呈现增长趋势,且与冻融作用次数之间符合指数函数关系;相比于NC,SCC的冻融损伤变量增长速率较小;掺入UEA和VEA可以有效降低SCC冻融损伤的发展速率。
[1] 商怀帅, 欧进萍, 宋玉普. 混凝土结构冻融损伤理论及冻融可靠度分析[J]. 工程力学, 2011, 28(1): 70−74. SHANG Huaishuai, OU Jinping, SONG Yupu. Analysis on reliability and freeze-thaw damage theory of concrete[J]. Engineering Mechanics, 2011, 28(1): 70−74.
[2] 杜鹏, 姚燕, 王玲, 等. 混凝土冻融损伤演化方程的初步建立[J]. 材料科学与工程学报, 2013, 31(4): 540−543. DU Peng, YAO Yan, WANG Ling. Initial establishment of freeze-thaw damage evolution equation of concrete[J]. Journal of Materials Science and Engineering, 2013, 31(4): 540−543.
[3] 田威, 谢永利, 党发宁. 冻融环境下混凝土力学性能试验及损伤演化[J]. 四川大学学报(工程科学版), 2015, 47(4): 38−44. TIAN Wei, XIE Yongli, DANG Faning. Experiment study on the mechanical property damage evolution of concrete under freeze-thaw environment[J]. Journal of Sichuan University (Engineering Science Edition), 2015, 47(4): 38−44.
[4] 冀晓东, 宋玉普, 刘建. 混凝土冻融损伤本构模型研究[J]. 计算力学学报, 2011, 28(3): 461−467. JI Xiaodong, SONG Yupu, LIU Jian. Study on frost damage constitutive model of concrete[J]. Chinese Journal of Computation Mechanics, 2011, 28(3): 461−467.
[5] 关宇刚, 孙伟, 缪昌文. 基于可靠度与损伤理论的混凝土寿命预测模型Ⅰ: 模型阐述与建立[J]. 硅酸盐学报, 2001, 29(6): 530−534. GUAN Yugang, SUN Wei, MIAO Changwen. One service-life prediction model for the concrete based on the reliability and damage theoriesⅠ: narration and establishment of the modelⅡ[J]. Journal of the Chinese Ceramic Society, 2001, 29(6): 530−534.
[6] 关宇刚, 孙伟, 缪昌文. 基于可靠度与损伤理论的混凝土寿命预测模型Ⅱ:模型验证与应用[J]. 硅酸盐学报, 2001, 29(6): 535−540. GUAN Yugang, SUN Wei, MIAO Changwen. One service-life prediction model for the concrete based on the reliability and damage theoriesⅡ: verification and application of the modelⅡ[J]. Journal of the Chinese Ceramic Society, 2001, 29(6): 535−540.
[7] DUAN An, TIAN Ye, DAI Jianguo, et al. A stochastic damage model for evaluating the internal deterioration of concrete due to freeze-thaw action[J]. Materials and Structures, 2014, 47(6): 1025−1039.
[8] PENTTALA V. Surface and internal deterioration of concrete due to saline and non-saline freeze-thaw loads[J]. Cement and Concrete Research, 2006, 36(5): 921−928.
[9] YU Hongfa, MA Haoxia, YAN Kun. An equation for determining freeze-thaw fatigue damage in concrete and a model for predicting the service life[J]. Construction and Building Materials, 2017, 137: 104−116.
[10] 张萌, 刘清, 韩风霞, 等. 自密实混凝土冻融循环后基本力学性能试验研究[J]. 混凝土, 2016(12): 22−24. ZHANG Meng, LIU Qing, HAN Fengxia, et al. Study on the basic mechanical properties of self-compacting concrete after freeze-thraw cycles[J]. Concrete, 2016(12): 22−24.
[11] 薛瑞. 自密实混凝土冻融循环作用后的力学性能研究[D]. 哈尔滨: 哈尔滨工业大学土木工程学院, 2012: 36−45. XUE Rui. The mechanical properties of self-compacting concrete after freeze-thaw cycles[D]. Harbin: Harbin Institute of Technology. School of Civil Engineering, 2012: 36−45.
[12] 邢凯. 冻融循环下混凝土力学性能试验及损伤演化研究[D]. 西安: 长安大学建筑工程学院, 2015: 17−23. XING Kai. Experimental study on mechanical properties and damage evolution of concrete under freezing-thawing[D]. Xi’an: Chang’an University. School of Civil Engineering, 2015: 17−23.
[13] 祝金鹏, 李术才, 刘宪波, 等. 冻融环境下混凝土力学性能退化模型[J]. 建筑科学与工程学报, 2009, 26(1): 62−67. ZHU Jinpeng, LI Shucai, LIU Xianbo, et al. Mechanical property deterioration model for concrete in environment with freezing-thawing[J]. Journal of Architecture and Civil Engineering, 2009, 26(1): 62−67.
[14] 邹超英, 赵娟, 梁锋, 等. 冻融作用后混凝土力学性能的衰减规律[J]. 建筑结构学报, 2008, 29(1): 117−123. ZOU Chaoying, ZHAO Juan, LIANG Feng, et al. Degradation of mechanical properties of concrete caused by freeze-thaw action[J]. Journal of Building Structure, 2008, 29(1): 117−123.
[15] LEMAITRE J. How to use damage mechanics[J]. Nuclear Engineering and Design, 1984, 80(2): 233−245.
[16] 余寿文. 损伤力学[M]. 北京: 清华大学出版社, 1997 : 26−32. YU Shouwen. Damage mechanics[M]. Beijing: Tsinghua University Press, 1997: 26−32.
[17] 曹文贵, 张升, 赵明华. 基于新型损伤定义的岩石损伤统计本构模型探讨[J]. 岩土力学, 2006, 27(1): 41−46. CAO Wengui, ZHANG Sheng, ZHAO Minghua. Study on statistical damage constitutive model of rock based on new definition of damage[J]. Rock and Soil Mechanics, 2006, 27(1): 41−46.
[18] COMMITTEE R T. Final report of RILEM TC 205-DSC: durability of self-compacting concrete[J]. Materials and Structures, 2008, 41(2): 225−233.
[19] 游宝坤, 陈富银, 韩立林, 等. UEA水泥砂浆与混凝土长期性能的研究[J]. 硅酸盐学报, 2000, 28(4): 314−318. YOU Baokun, CHEN Fuyin, HAN Lilin , et al. Investigation of the long-term properties of UEA cement mortar and concrete[J]. Journal of the Chinese Ceramic Society, 2000, 28(4): 314−318.
(编辑 伍锦花)
Uniaxial compression damage constitutive model of concrete subjected to freezing and thawing
LONG Guangcheng, LIU He, MA Kunlin, XIE Youjun
(School of Civil Engineering, Central South University, Changsha 410075, China)
In order to study the stress-strain property and bearing capacity of concrete after freeze-thaw cycles, compression stress-strain properties of normal concrete(NC) and self-compacting concrete(SCC) during freezing and thawing cycles were compared. Furthermore, an uniaxial compression damage constitutive model was established based on strain equivalence hypothesis and statistical damage theory. Evolution characteristics of corresponding damage variable with different freezing and thawing cycles and uniaxial compressive strains were discussed. The results show that strain-stress characteristics of NC and SCC during freezing and thawing cycles are effectively described by the proposed damage constitutive model. During the process of uniaxial compression, the growth rate of damage variable decreases slightly as the microcracks caused by freezing-thaw are closed by the vertical pressure. Variation law of freezing and thawing damage of NC and SCC during freezing and thawing cycles can be predicted by exponential function. Damage rate of SCC is reduced effectively by incorporation of expansion agent and viscosity modification materials.
freezing-thawing cycle; stress-strain curve; uniaxial compression damage constitutive model; self-compacting concrete
TU528.53
A
1672−7207(2018)08−1884−09
10.11817/j.issn.1672−7207.2018.08.007
2017−09−11;
2017−11−19
中国铁路总公司科技研究开发计划项目(2016G001-C);国家自然科学基金资助项目(51678586,51678569) (Project(2016G001-C) supported by the Research and Development Plan of China Railway Corporation; Projects(51678586, 51678569) supported by the National Natural Science Foundation of China)
龙广成,博士,教授,从事先进水泥基材料及混凝土耐久性研究;E-mail:565410408@qq.com
