软件定义数据中心网络基于分支界限法的多路径路由算法
2018-09-07雷田颖林子薇何荣希
雷田颖,林子薇,何荣希
(大连海事大学 信息科学技术学院,辽宁 大连 116026) E-mail:cndlmu@sina.com
1 引 言
数据中心是云计算的支撑平台,而数据中心网络(Data Center Network,DCN)是连接数据中心大规模服务器进行大型计算的桥梁[1].DCN通常采用Fat-tree等具有“富连接”特点的拓扑,通过使用数量充裕的网络资源以提供可靠的转发服务[2].但传统的分布式控制,存在管理困难、资源利用率低等问题.基于OpenFlow的软件定义网络(Software Defined Network,SDN)是一种新型的网络架构,可实现数据层与控制层的解耦合,通过集中式控制器可获取全网状态信息,便于实现网络资源管理和网络流量分配等[3,4].因此,将SDN与DCN相结合的软件定义数据中心网络(Software-defined Data Center Network),可以更好地实现网络集中管理和流量优化等[5],已引起业界的极大关注.
SDCN中采用传统单路径算法分配路径,易造成数据过度集中,导致网络拥堵.因此,已有文献[6-10]提出多种多路径路由算法.文献[6]提出ECMP(Equal-Cost Multi-Path)算法,通过哈希运算和模运算计算转发路径,将数据流分散到不同路径传输,可在一定程度减少单路径算法导致的拥塞发生.但是,由于未考虑网络实时状态,可能将数据流分配到剩余带宽较少链路,仍易导致链路拥塞.文献[7]提出基于网络状态的OFMT(OpenFlow based Multipath Transmission)算法,通过周期性轮询和动态调度策略,可在一定程度避免链路出现拥塞和提高网络资源利用率.
文献[11]研究发现,DCN中的数据流可分为大象流(大流)和老鼠流(小流),其中大流所占比例约为10%,对吞吐量性能要求较高,而小流占据全部流量的绝大部分比例,对链路时延性能要求更高.然而,上述算法都未区分大、小流,忽视了其传输性能要求的差异性.为此,文献[8]和文献[9]提出SHR(Software-defined Hybrid Routing)算法和SCR(SDN-Based Classified Routing)算法,依据流截止时间以及等待队列长度为大流选路,而对小流则依据带宽计算概率随机选路.两种算法为大、小流提供不同选路策略,有利于满足其不同的传输性能需求.但是,算法的链路利用率不高.文献[10]提出MLF(Multi-path Routing on Link real-time status and Flow characteristics)算法,利用链路剩余带宽和哈希运算为大流选路,对小流则选择剩余带宽最大的路径.该算法可在一定程度上弥补文献[8,9]算法的不足.但是,仅依据链路剩余带宽为时延敏感的小流选路,很可能所选路径时延较大,导致小流传输时延性能不理想.
总的说来,上述算法[6-10]有一些不区分数据流大小及其对传输性能要求的差异性,对所有数据流采用相同选路策略,而有些则只片面强调大流的吞吐量指标、小流的时延指标.事实上,对于大流而言,选择剩余带宽较大路径对于提高吞吐量固然重要,但其时延性能也不容忽视.为大流选路时,如果适当考虑时延因素,选择时延较小路径,可以使其更快完成传输,从而使后续到达大流具有更多可用带宽资源,有利于提高其吞吐量.相应地,对于小流而言,不仅要关注其时延性能,满足其时延敏感特性,也应酌情考虑路径剩余带宽情况,尽可能选择剩余带宽较大路径,达到更为理想的负载均衡效果.另外,DCN是一个连接数万级、十万级甚至百万级的大规模服务器群,规模巨大,因此,如何减少路由算法的时间复杂度也是设计时应该考虑的一个重要因素.分支限界法[12]是一种全局求解算法,基于灵活的回溯机制,可在局部无解时回到更高层次以调整搜索范围,通过一定规则扩展子节点,并访问尽可能少的节点,因此,有利于减少寻找可行解或者最优解的次数.本文将分支界限法的思想引入SDCN多路径路由算法中,首先利用分支限界法的思想从原网络获取一个网络子集,然后在该子集为数据流选择合适路径.由于该子集所包含节点和链路数远小于原网络,因此,可以减少算法为每一个数据流选路的求解次数,有利于降低算法的时间复杂度.
本文利用SDN控制器掌控全网状态信息的优势,综合考虑大、小流对传输性能的不同要求,针对SDCN提出一种基于分支界限法的多路径路由算法(Multiple path routing algorithm based on branch and bound,MPA-BB).首先,利用分支限界法思想获取链路剩余带宽尽可能大、链路时延尽可能小的网络子集.为了保证子集中任意服务器间均可通信,提出最小网络连通子集概念,并给出SDCN连通条件.然后,依据大、小流各自的性能要求,提出瓶颈时延、瓶颈带宽等概念,在此基础上在网络子集中为大、小流利用不同策略选择合适路径.最后,通过Mininet和Floodlight进行仿真测试,仿真结果表明:与文献中已有算法相比,MPA-BB算法具有更低的分组端到端时延、更高的网络吞吐量和平均链路利用率.
2 MPA-BB算法
2.1 SDCN连通性分析
基于Fat-Tree拓扑的SDCN由交换机、服务器以及连接它们的双向链路构成.由于服务器是数据流的源和目的节点,而服务器直接与边缘层交换机相连.为了保证数据正常通信,服务器与边缘层交换机之间必须一直处于连接状态,即可行网络子集中必须包含所有边缘层交换机和服务器,且处于连接状态.进而,要保证可行网络子集中所有服务器间均连通,必须保证与源服务器直接相连的边缘层交换机和与目的服务器直接相连的边缘层交换机之间均连通.为此,将SDCN中由交换机及其连接链路构成的网络子集记为初始网络G0=(N,L).G0从上至下可分为核心层、汇聚层和边缘层,其中N=C∪A∪E,表示所有交换机构成的节点集合,交换机数为|N|.C、A、E分别为核心层、汇聚层和边缘层交换机的集合,C∩A=C∩E=A∩E=Φ,各个集合包含交换机数分别为|C|、|A|、|E|.L表示连接各个交换机节点的双向链路(边)的集合,链路数为|L|.如果两个节点之间存在双向边,则称两节点已连接;否则,则表示其未连接.Fat-Tree拓扑将汇聚层交换机和边缘层交换机分为若干集合,每一个集合称为一个pod(point of delivery)[2].对于有k个pod的Fat-Tree拓扑,G0中|N|=(5k2/4),|C|=(k/2)2,|A|=k2/2,|E|=k2/2,|L|=k3/2,服务器k3/4个,任意两个边缘层交换机间共有k2/4条可行路径,如图1所示.图中,边缘层、汇聚层、核心层交换机依次编号1到k2/2、k2/2+1到k2和k2+1到5k2/4.每个pod含有k个交换机(汇聚层和边缘层交换机各k/2个).将核心层交换机依次排列,每k/2个交换机为一组,共k/2组,每一组连接不同pod中同一位置的汇聚层交换机.用a[i][j](1≤i,j≤5k2/4)表示网络中第i个交换机与第j个交换机的连接情况.如果i和j相连(即连通),其值为1;否则,其值为0.

图1 具有k个pod的Fat-tree拓扑图Fig.1 Fat-tree topology with k pods
MPA-BB算法的目的是综合考虑链路时延和剩余带宽因素,获取符合大、小流传输特性的最佳路径.为了降低算法复杂度,首先利用分支限界法思想从G0中获取一个网络子集,进而在该子集中为数据流选择可行路径.在利用分支限界法选择网络子集时,必须要保证网络中所有服务器对间均能正常通信(即保证SDCN全连通).在描述SDCN全连通条件前,引入以下定义.
定义1.最小网络连通子集.在G0中,如果只有一个核心层交换机,每一个pod中只有一个汇聚层交换机,并均与该核心层交换机相连接,而且每一个汇聚层交换机又与该pod中所有边缘层交换机相连接,则称该网络子集为最小网络连通子集.由Fat-Tree拓扑的特点可知,它包含|C|个最小网络子集.
由最小网络连通子集的定义可知,要保证全网边缘层交换机全部连通,只需要保证利用分支界限法获取的最佳网络子集中至少包含一个最小网络连通子集即可.
定理1.为了保证SDCN中边缘层交换机全连通,必须同时满足以下两个条件:
条件1.存在j∈{k2+1,k2+2,…, 5k2/4},使得式(1)成立.
(1)
条件2.对于任意的n∈{0,1,2,…,k-1},使得式(2)成立.
(2)
其中,
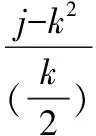
(3)
其中,j必须是满足条件1的核心层交换机.式(3)保证满足条件1的核心层交换机j与每一个pod中第m个汇聚层交换机相连接.
证明:根据核心层交换机与汇聚层交换机的连接特点和数据流的转发特点可知,条件1要求至少存在一个核心层交换机与其所有连接的汇聚层交换机均处于工作状态,即保证核心层与汇聚层连通.
根据汇聚层交换机与边缘层交换机的连接特点可知,条件2要求条件1中所有满足要求的核心层交换机中,至少有一个核心层交换机连接的所有汇聚层交换机分别与本pod中所有边缘层交换机连接,即保证podi(1≤i≤k)内部边缘层交换机全连通.
因此,当且仅当同时满足条件1和条件2时,处于工作状态的网络子集至少包含一个最小网络连通子集,因此可保证SDCN中边缘层交换机连通,即保证了SDCN中服务器连通,也就是保证了SDCN连通.
2.2 算法描述
为了更好地对算法进行描述,引入以下定义.
定义2.瓶颈时延.构成路径r的链路集合为L′={l1,l2,…,lj},链路li的时延为di,则dr=max{di},li∈L′称为r的瓶颈时延.
定义3.瓶颈带宽.构成路径r的链路集合为L′={l1,l2,…,lj},链路li的剩余带宽为bi,则br=min{bi},li∈L′称为r的瓶颈带宽.
MPA-BB算法首先利用分支限界法思想获取一个保证SDCN连通的网络子集,然后根据网络状态信息和大小流各自的性能要求为其提供不同的选路策略.分支限界法的主要思想是以最小代价优先方式搜索问题的解空间树,每一个活节点只有一次机会成为扩展节点.活节点一旦成为扩展节点,就一次性产生其所有子节点.将这些子节点中导致不可行解或导致非最优解的子节点舍弃,其余子节点加入活节点表.此后从活节点表中取下一个节点成为扩展节点,并重复上述节点扩展过程,直到找到所需解或活节点表为空[12].
MPA-BB主要由拓扑管理模块(Topology Management,TM)、连通性判断模块(Connection Judgement,CJ)、路由管理模块(Routing Management,RM)和流表下发模块(Flow Distribution,FD)组成,整体架构如图2所示.

图2 算法总体架构Fig.2 Overall architecture of the algorithm
TM模块是MPA-BB算法的基础模块,首先对整个SDCN进行感知,获取核心层、汇聚层、边缘层交换机的连接方式和网络中每条链路的时延信息,并利用sflow软件*sflow [OL].[2017-07-06].http://www.sflow.org/获取每条链路的剩余带宽信息.然后,考虑到SDCN中数据流存在大流和小流之分,因此根据获取到的信息,利用分支限界法思想分别获取满足大流和小流性能需求的最佳网络子集Gbest1和Gbest2,并将Gbest1和Gbest2中任意两个边缘层交换机i和j(1≤i,j≤k2/2)之间所有可行路径分别存放到集合Bij和Sij,以供RM模块使用.这样当有数据流需要控制器为其选路时,RM模块只需判断该数据流为大流还是小流(1~100KB为小流,大于100KB为大流[11]),即可根据该数据流的源和目的节点从相应的集合Bij或者Sij中依据对应的选路策略选择一条最佳路径.
由于大流对吞吐量要求较高,因此首先考虑链路剩余带宽的影响.此时,可通过分支限界法从G0中获取满足式(4)要求的网络子集G1.具体过程为:初始化G1=G0,将所有核心层交换机节点存放到活节点集合Jc1中,从该集合依次取出每一个核心层交换机节点.以该节点为根节点,相连的汇聚层交换机节点为末节点,查看二者之间链路的剩余带宽是否满足式(4).如果满足,则将该末节点存放到活节点集合Ja1中;否则,从G1中删除该链路,更新G1.值得注意的是,每一次将汇聚层节点放入集合Ja1时,需要判断集合中是否已经含有该节点.只有当集合中没有该节点时才将此节点放入集合.当Jc1为空时,从Ja1中依次取出每一个汇聚层交换机节点,以该节点为根节点,相连的边缘层交换机为末节点,查看二者之间链路的剩余带宽是否满足式(4).如果满足,由于边缘层交换机节点为网络的最底层节点,已无子节点,所以回到汇聚层交换机节点,继续查看其他链路;否则,从G1中删除该链路,更新G1.当Ja1为空时,此时的G1即为G0中满足式(4)条件的网络子集.
对于大流而言,考虑到如果适当选择时延较小路径,可以使其更快完成传输,也有利于网络吞吐量的提高.因此,继续考虑链路时延的影响,通过分支限界法从G1中获取满足式(5)的网络子集G2,将G2记为大流的最佳网络子集Gbest1.具体过程与获取G1的过程类似,即初始化G2=G1,首先以每一个核心层交换机为根节点,从G2中获取满足式(5)要求的所有汇聚层交换机节点并存放到集合Ja2中,同时删除不满足要求的连接核心层和汇聚层交换机的链路,更新G2.然后以Ja2中每一个节点为根节点,删除所有不满足式(5)要求的连接汇聚层和边缘层交换机的链路,更新G2,此时G2即为Gbest1.
最后,从Gbest1中获取任意边缘层交换机间传输大流时的所有可行路径,存放到集合Bij(1≤i,j≤k2/2).获取Gbest1和Bij的伪代码如下:
Input:G0;
Output:Bij;
begin
G1←G0;
forcinJc1do
ifbi≥bminthen
ifJa1.contains(a)==falsethen
Ja1.add(a); //a是c所连接的汇聚层节点
endif
else
deletelacfromG1;//lac为a和c相连的链路
flag=CJ(G1);//CJ函数用于判断链路是否可删除
ifflag==falsethen
G1.add(lac);
endif
endif
endfor
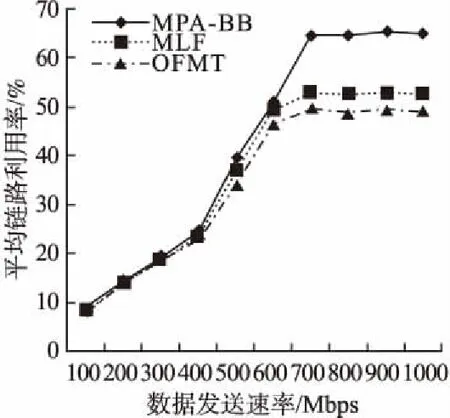
forainJa1do
ifbi deletelfromG1;//l为a和边缘层交换机相连的链路 endif flag=CJ(G1); ifflag==falsethen G1.add(l); endif endfor G2←G1; forcinJc2do ifdi≤dmaxthen ifJa2.contains(a)==falsethen Ja2.add(a); endif else deletelacfromG2; flag=CJ(G2); ifflag==falsethen G2.add(lac); endif endif endfor forainJa2do ifdi>dmaxthen deletelfromG2; endif flag=CJ(G2); ifflag==falsethen G2.add(l); endif endfor Gbest←G2; Bij=getRoutes(Gbest); returnBij; 值得注意的是,在分支限界法的过程中一旦要删除某条链路,则需利用CJ模块判断剩余网络资源所构成子集是否满足定理1给出的SDCN连通条件.因此,当网络中的链路均不满足式(4)和(5)时,则Gbest1是以Core中最后一个节点为根节点的最小网络连通子集.由于本模块处于SDN集中控制器中,而控制器每隔一定时间T将会重新感知整个网络,因此,本模块每隔T重新调用一次. 对于小流,则首先应考虑其时延性能,其次再兼顾剩余带宽.获取满足小流性能要求的最佳网络子集Gbest2和任意边缘层交换机间传输小流的可行路径集合Sij的过程与上述过程类似,由于小流对时延更为敏感,因此,此时先从G0中获取满足式(5)的子集G1,然后,再从G1中获取满足式(4)的子集G2,最终从G2中找出Gbest2,并从Gbest2中获取任意边缘层交换机间的可行路径集合Sij. bi≥bmin (4) di≤dmax (5) 其中,bmin(min{bi}≤bmin≤max{bi},li∈L)和dmax(min{di}≤dmax≤max{di},li∈L)均为常数,可根据网络实际状况设定.bmin表示所有链路剩余带宽的下限值,其值越大,则选路时对链路剩余带宽的要求越高.dmax表示所有链路的最大时延,其值越小,则选路时对链路时延的要求越高. 2Floodlight Editor, Floodlight Manual [OL].[2017-07-03], http://www.projectfloodlight.org. CJ模块主要用于对网络连通性进行判断,即利用定理1的条件判断所有服务器是否能正常通信.当满足SDCN全连通条件时,本模块返回True,否则返回False. RM模块主要为数据流f选取最佳路径,伪代码如下: Input:f; Output:Rbest; begin i← getSource(f); //获取数据流的f的源节点 j← getDes(f); //获取数据流的f的目的节点 ifsize(f)>ωthen//ω为大小流的分界值 Rbest← getBest(Bij); else Rbest← getBest(Sij); endif returnRbest; 当数据流f需控制器为其选路时,获取对应的源、目的边缘层交换机节点i和j,并判断其为大流还是小流(1~100KB为小流,大于100KB为大流[11]): 1)如果为大流,则利用sflow获取Bij中所有路径的实时瓶颈带宽,然后选择瓶颈带宽最大的路径为最佳路径Rbest,供FD模块使用. 2)如果为小流,则从Sij所有路径中选择瓶颈时延最小的路径为最佳路径Rbest,供FD模块使用. 现对控制器为每一条数据流选路过程的复杂度进行分析.假设Bij或者Sij中含有f(1≤f≤k2/4)条可行路径,因此,需要进行f-1次比较以获取性能最佳路径,时间复杂度为O(f).最坏情况是G0为最佳网络子集,此时Bij或者Sij中存在k2/4条可行路径,此时,时间复杂度为O(k2/4). FD模块根据Rbest生成流表信息,并告知相应的交换机如何对数据流进行传输. 采用Mininet[13]仿真软件搭建SDCN,采用Floodlight2作为集中控制器,对本文所提出的MPA-BB算法进行仿真评测,并与OFMT算法[7]和MLF算法[10]进行对比.仿真拓扑采用k=4的Fat-Tree拓扑,包含16个主机、20个交换机和32条链路.仿真中,每条链路的时延在1到10ms之间随机产生,链路带宽为1Gbps,dmax=5ms,bmin=500Mbps.仿真中T=5s,利用ping技术和Iperf软件产生数据流量.随机选取10对服务器分别作为数据流的源和目的服务器.根据Benson等人的研究成果[11],假设90%的流大小为1~100KB(即小流),10%的流大小大于100KB(即大流),都服从均匀分布.小流持续时间为2秒,大流持续时间为10秒.在不同发送速率下对算法进行仿真比较,仿真评测指标为分组端到端时延、网络吞吐量和平均链路利用率.每种发送速率都进行10次实验,取10次的平均值作为仿真结果,如图3-图5所示. 图3表示不同发送速率下各算法的分组端到端时延情况.从图中可以看出:随着发送速率增大,各个算法的时延均呈上升趋势.但是,MPA-BB算法最低,OFMT算法最高,而MLF位于二者之间.主要原因在于:网络带宽一定时,随着发送速率的增加,网络负载随之增加,网络中会出现一定程度的拥堵,因此各个算法的时延均会有所增加.由于MPA-BB算法在选路过程中充分考虑链路时延和剩余带宽的影响,优先尝试删除时延较大和剩余带宽较小的链路以获取网络子集,因此,所选路径包含高时延和低剩余带宽的链路较少.另外,MPA-BB算法选路时,对大流选取瓶颈剩余带宽较大路径,对小流优先获取瓶颈时延较小路径,可以最大限度地避免选取路径剩余带宽不足或者时延较大而导致大量数据等待,所以分组端到端时延性能优于其他两种算法.由于OFMT算法未区分对待大小流,未充分利用网络状态信息选路,因此,分组端到端时延性能较差.虽然MLF算法考虑了大、小流的差异性,对大流考虑链路剩余带宽因素影响,但是采取哈希运算为其选路,可能导致数据集中在某些链路,因此,容易导致大流分组端到端时延不理想.而对小流则直接选取剩余带宽较大的路径,所选路径时延可能较大,因此,会影响小流的时延性能,所以整体上MLF算法的分组端到端时延位于MPA-BB和OFMT之间. 图3 分组端到端时延Fig.3 End to end delay of packets 图4 网络吞吐量Fig.4 Network throughput 图5 平均链路利用率Fig.5 Average link utilization 图4给出了不同发送速率下各算法的网络吞吐量对比情况.从图中可以看出:当发送速率较小时(低于500Mbps),各算法的吞吐量性能相差不大.但是,随着发送速率逐渐增大,各算法的吞吐量均有不同程度上升,而且差距逐渐明显(MPA-BB最大、MLF次之、OFMT最低).当发送速率达到500Mbps时,网络吞吐量达到最大值.继续增加发送速率,由于网络出现拥塞,吞吐量逐渐下降,并趋于稳定.由于MPA-BB算法综合考虑了链路时延和链路剩余带宽对数据流的影响,尽可能选取负载轻、时延小的路径转发数据流,因此其吞吐量性能优于其他两种算法. 图5对比了不同发送速率下各算法的平均链路利用率性能.从图中可以看出:当发送速率较小时(低于400Mbps),由于网络负载较轻,三种算法的链路利用率较低,而且相差不大.但是,随着数据发送速率逐渐增大,网络负载逐渐增加,三种算法的利用率均有不同程度上升,而且差距逐渐明显(MPA-BB最大、MLF次之、OFMT最低).当发送速率较大时(高于500Mbps),网络负载较重,各链路已用带宽较大,因此链路利用率均较高.由于MPA-BB算法充分考虑了链路剩余带宽对数据流的影响,尽可能选取负载轻的路径转发数据流,当网络负载较高时,可以将数据流分配到其他已用带宽较小的链路上传递数据,有利于接纳更多大流,因此平均链路利用率高于其他两种算法. 本文针对SDCN中数据流的特点,提出一种基于分支界限法的多路径路由算法(MPA-BB),该算法针对大、小流不同的网络性能需求,综合考虑时延和剩余带宽两种因素的影响,为大、小流采用不同的选路策略选择合适的路径.最后,通过Mininet和Floodlight进行仿真评测,结果表明:与文献中已有算法相比,MPA-BB算法在传输数据包过程中具有更低的分组端到端时延、更高的网络吞吐量和平均链路利用率.考虑到基于Fat-Tree拓扑的DCN会增加网络能耗,不利于实现绿色节能,因此,下一步将对节能路由进行研究.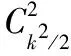
3 仿真实验与性能分析


4 结束语
