采用个体进化状态判定策略的分解类多目标进化算法

李浩君，刘中锋，王万良，张 征，张鹏威

1(浙江工业大学 教育科学与技术学院，杭州 310023) 2(浙江工业大学 计算机科学与技术学院，杭州 310023) E-mail：zgdlhj@zjut.edu.cn

1 引 言

在很多现实应用中，多目标问题(MOP)需要同时优化多个目标[1]，这些目标通常是彼此冲突的，没有一个单一解可以同时优化所有目标.Pareto最优解是不同目标之间最好的折中候选解，多目标进化算法(MOEAs)能够在单次运行中发现一组有代表性的Pareto最优解，能够有效解决MOP问题，因此很多MOEAs算法[2-4]已经被提出.

大多数现有MOEAs算法将MOP问题作为一个整体，利用快速非支配排序方法进行优化[5,6].这些MOEAs算法具有较好的收敛性，但分布性较差，不能较好地平衡全局探索和局部开发，易收敛到局部Pareto前沿[7].一个MOP问题的Pareto最优解可能是一个标量问题的最优解，因此可以将MOP问题分解为多个标量子问题.Zhang和Li[8]提出了基于分解方法的分解类多目标进化算法(MOEA/D)，MOEA/D算法将MOP问题分解为N个标量子问题，每一个子问题通过使用其邻域信息进行优化，每一个子问题在当前种群中都有其目前发现的最优解，所有子问题的最优解组成MOP问题的Pareto最优解集，已经证明MOEA/D算法具有更低的计算复杂度[9-12].

将差分进化算法的多种变异算子应用于MOEA/D是分解类多目标优化领域的一个方向.Li和Zhang[13]提出分解类多目标差分进化算法(MOEA/D_DE)，MOEA/D_DE算法将差分进化算法的一组变异算子引入MOEA/D算法框架，提高了算法的收敛性和多样性；目前已经有很多研究致力于通过变异算子提高MOEAs算法性能[14-16]，但已有的研究主要采用随机选择机制选择变异算子，不能保证优质解的产生.为了解决这一问题，刘志军等[17]提出采用概率匹配策略自适应地为多目标差分进化算法选择变异算子，概率匹配策略将变异算子所生成成功进入下一代解的个数作为历史信息，并将历史信息转化为变异算子被选择的概率，从而为个体选择具有较高生成成功子代概率的变异算子.Li等[18]提出老虎机策略用于自适应地为算法选择变异算子，该策略将进化过程中适应度变化的历史信息，作为变异算子被选择的依据.

MOEA/D算法中变异算子的选择，参考生成成功子代的历史信息，可以提高特定阶段内较好变异算子的选择概率，能够在一定程度上提高算法的性能.但是历史信息不能完全反映个体的当前进化状态，利用历史信息为个体选择变异算子，不能保证算法获得真实的Pareto最优解集.为了克服已有变异算子选择策略对个体当前进化状态信息利用不足的问题，本文提出了采用个体进化状态判定策略的分解类多目标进化算法(MOEA/D_PE).MOEA/D_PE算法采用个体进化状态判定策略提高算法选择合适变异算子的能力，从而保证算法具有较好的收敛性和多样性.个体进化状态判定策略是：首先，根据个体与其邻域内其它个体标量子问题函数值的大小关系，确定个体属于进化程度较好、较差或一般的概率，从而判定个体的进化状态；然后，根据个体进化状态为个体选择合适的变异算子.个体进化状态判定策略，充分考虑了个体的当前进化信息，提高了算法平衡全局探索和局部开发的能力，能够保证算法获得的Pareto前沿过程中具有良好的收敛性和多样性.

2 MOEA/D算法

MOEA/D算法利用传统分解方法将MOP问题分解为一些标量子问题，利用子问题之间的邻域信息优化MOP问题.

2.1 MOP问题

一个多目标问题(MOP)具有多个待优化的目标.一个MOP问题可以被数学表达为如下：

minimizeF(x)=(f1(x)，…，fm(x))

subjecttox∈Ω

(1)

其中x=(x1，…，xn)∈Rn是一个决策变量向量，Ω是搜索空间的可行域，F：Ω→Rm是由m个目标函数f1(x)，…，fm(x)组成.如果Ω是一个在Rn上封闭并且联通的区域，而且所有目标是x上连续的，这一问题可以被称为一个连续的MOP问题.x，y∈Ω，当且仅当fi(x)≤fi(y)对于所有i∈{1，…，m}成立，并且F(x)≠F(y)时，称x支配y，表示为x≻y.一个点x*∈Ω，如果没有其他x∈Ω支配x*，则称x*为Pareto最优解.所有Pareto最优解的集合被称为Pareto最优解集(PS)，Pareto前沿(PF)被定义为PF={F(x)|x∈PS}[1].

2.2 Tchebycheff分解方法

在MOEA/D算法中，一个MOP问题被分解为N个标量子问题，MOEA/D算法优化这些标量子问题得到的最优解集近似真实PF[8，19，12].很多分解方法已经被应用在MOEA/D算法框架中[8，20，21].其中，最为经典的是Tchebycheff分解方法，该方法如公式(2)所示.

subjecttox∈Ω

(2)

2.3 邻 域

因为在Tchebycheff分解方法中每一个子问题与方向向量相关，并且它的目标函数是方向向量上连续的，如果两个子问题的方向向量靠近，可以假设这两个子问题具有相似的最优解.利用这一假设，MOEA/D引入了一个邻域概念[8].给定一个子问题，它的邻域是方向向量与其方向向量之间的欧氏距离最近子问题的集合，邻域内的子问题是它的邻居.

3 MOEA/D_PE算法

MOEA/D_PE算法是在MOEA/D算法框架基础上，采用个体进化状态判定策略，判定个体的进化状态，为个体自适应选择符合其进化状态的变异算子.

3.1 个体进化状态判定策略

MOP问题包含多个相互冲突的子目标，个体解之间不能直接比较，为了获得个体解之间的差异，MOEA/D算法通过分解方法将MOP问题转换为多个标量子问题，如公式(2).gte(x|λ，z*)在方向向量上是连续的，所以方向向量相邻的子问题可能具有相似的解，同时不同解之间的差异可以通过标量子问题的函数值gte(x|λ，z*)进行直接比较.

个体进化状态判定策略，是根据当前个体与其邻域内多个其它个体标量子问题函数值的大小关系，确定个体属于较好、一般和较差进化状态的概率，根据个体属于较好、一般和较差进化状态的高概率判定个体进化状态，根据已有的进化状态判定结果，为个体选择合适的变异算子.

如果个体标量子问题的函数值优于随机三个邻域内其他个体，则该个体具有属于较好个体的高概率，判定该个体具有较好进化状态；如果个体标量子问题的函数值均差于邻域内三个其他个体，该个体具有属于较差个体的高概率，判定个体属于较差进化状态；否则判定个体属于一般进化状态.

不同的变异算子具有不同的探索和开发能力.公式(3)是具有较好探索能力的变异算子，公式(4)是具有较好开发能力的变异算子，而公式(5)是一次平滑函数，不具有明显的探索和开发能力，但可以对数据进行平滑处理.个体进化状态判定策略是首先判定个体进化状态，然后为个体选择合适的变异算子；当个体进化程度较好，应利用公式(4)进行开发操作，以加速收敛；当个体进化程度较差，利用公式(3)对个体进行探索操作；当个体属于一般进化状态时，利用公式(5)对种群进行平滑处理，提高种群的多样性.

vi=xi+F×(xr1-xr2)

(3)

vi=xi+K×(xi-xr1)+F×(xr2-xr3)

(4)

vi=α×xr1+(1-α)×xr2

(5)

xi为当前个体i的目标向量，xr1、xr2和xr3是个体i邻域内彼此不同且不同于xi的三个目标向量，F为缩放因子取值为0.5，K也是缩放因子，在本文中取值为0.5，α是[0 1]区间上的一个随机数.

3.2 MOEA/D_PE框架

3.2.1 初始化操作

初始化算法种群和权重向量，令参考点等于个体中最优适应度值；将种群中的Pareto最优解放入外部种群EP；

3.2.2 更新操作

第1步.任意个体i，从其邻域内随机取3个不同个体的目标向量xr1、xr2和xr3，比较个体i的目标向量xi，与xr1、xr2、xr3在标量子问题函数值的大小关系，利用个体进化状态判定策略判定个体属于邻域内较好、较差和一般进化状态的概率，进而判定个体进化状态；

第2步.根据个体进化状态，为个体i选择合适的变异算子，进行遗传操作(变异和交叉)以生成新解y；如果y的标量子问题函数值优于参考点，则将y的标量子问题函数值赋值到参考点；

第3步.比较y与个体i邻域内所有个体标量子问题函数值的大小关系，如果个体标量子问题函数值差于y，则将y替代该个体；

第4步.如果y支配EP中的个体，则从EP中移除被支配的个体，并将y添加到EP中；

第5步.重复更新操作；

3.3.3 终止操作

如果满足终止条件满足，终止迭代，并输出EP；否则跳转到更新操作.

4 实验研究

本文所有实验中用到的算法和适应度函数均采用MATLAB语言编码，利用配备了2.5GHZ Intel Core (TM) i5-2450M CPU的计算机进行实验.为了评估MOEA/D_PE算法的性能，本文选择了7个测试函数[22](MOP1～MOP7)，并将MOEA/D_PE算法与MOEA/D_DE算法[13]、最新分解类多目标进化算法MOEA/D_FRRMAB算法[18]和最新非支配排序类多目标遗传算法NSGA-III算法[23]进行了比较.

4.1 实验设置

1)种群大小N：在二目标的测试问题中所有算法种群大小被设置为100，而三目标测试问题中，所有算法的种群大小都被设为300.

2)交叉、变异算子：MOEA/D_DE、NSGA-III、MOEA/D_FRRMAB等算法的交叉算子和变异算子参考原文献，MOEA/D_PE算法根据个体进化状态判定策略选择变异算子，交叉算子参考文献[12].

3)终止条件：所有算法最大评估次数为3000.

4)所有算法在每一个测试问题中均独立运行30次.

4.2 性能度量

采用翻转时代距离(IGD)[24，25]评估算法的性能.假设P*是目标空间中均匀分布在PF上的一组Pareto最优解.假设P是算法获得的，一组近似PF的解集.从P*到P的IGD被定义为：

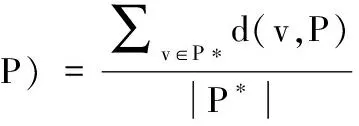
(6)

其中d(v，P)是v和P中的点之间最小的欧式距离.如果P*足够大，IGD(P*，P)可以同时测量P的收敛性和多样性[26].在二目标测试问题中，，选择了500个PF上均匀分布的点作为P*；在三目标测试问题中，选择1000个PF上均匀分布的点组成P*.

4.3 测试问题

本文所使用测试问题(MOP1-MOP7)均来自文献[22]，但本文对测试问题中的g(x)做了修改，使搜索空间为[0，1]n，n=10，MOP1-MOP5是具有两个目标的多目标测试问题，MOP6、MOP7是具有三个目标的多目标测试问题，详细内容如表1.

4.4 结果与讨论

表2显示了MOEA/D_DE、NSGA-III、MOEA/D_FRRMAB和MOEA/D_PE四个算法在每一个测试问题中30次独立运行IGD度量的方差和平均值.为了更好观察MOEA/D_PE算法与已有分解类多目标进化算法的差别，图1和2展示了MOEA/D_PE和MOEA/D_DE算法在MOP1-MOP7问题的收敛情况.

观察表2中的实验数据可知，MOEA/D_PE算法在5个二目标测试问题MOP1-MOP5中获得3个最优平均值，NSGA-III算法在MOP4中获得最优均值，MOEA/D_FRRMAB算法在MOP5中获得最优均值，MOEA/D_PE算法在MOP4和MOP5中的均值与最优值差别不大，这表明MOEA/D_PE算法在二目标测试问题中获得更好的精度.同时，MOEA/D_PE算法在二目标测试问题中获得2个最优方差，说明MOEA/D_PE算法表现出更好的稳定性.MOEA/D_PE算法在二目标测试问题中获得更好精度和稳定性的原因是，该算法能够准确判定个体进化状态，并为个体提供合适的变异算子，从而促进了个体进化.

表2 实验中各算法IGD度量的平均值和方差Table 2 Mean and variance of IGD measures for each algorithm in the experiment

从表2中三目标测试问题MOP6和MOP7中的实验数据可知，MOEA/D_PE算法获得全部最优均值，这表明MOEA/D_PE算法在三目标测试问题中能够实现较好的精度.同时，MOEA/D_PE算法在MOP7中获得了最优的方差，在MOP6中，MOEA/D_PE算法的方差仅次于MOEA/D_FRRMAB算法，这说明MOEA/D_PE算法在三目标测试问题中具有较好的稳定性.MOEA/D_PE算法在复杂的三目标测试问题中具有较好精度和稳定性的原因是，Tchebycheff分解方法将问题较好地分解，同时，个体进化状态判定策略则能够为个体选择合适的变异算子，最终，提高了MOEA/D_PE算法收敛精度和稳定性.

从图1二目标测试问题中可以看出，本文所提出的MOEA/D_PE算法在所有的二目标测试问题中都能收敛到全局Pareto前沿，而MOEA/D_DE算法在MOP4问题目标空间上失去了中间部分的Pareto前沿，未能表现出较好的收敛性能.图1(a)、(b)、(c)、(d)和(e)收敛情况表明，MOEA/D_PE算法获得的Pareto前沿更加均匀，这说明MOEA/D_PE算法在MOP1-MOP5二目标测试问题中具有更好收敛到全局Pareto前沿的性能.从图2可以观察到，在MOP6和MOP7三目标测试问题中，MOEA/D_PE算法也表现出了较好的收敛性能.这表明，充分利用个体的进化状态信息，根据不同的进化状态选择匹配的变异算子，能够有效提高算法收敛到全局Pareto前沿的性能和收敛稳定性.

图1 二目标测试问题MOP1-MOP5的算法收敛图Fig.1 Algorithm convergence figures of two objective test problems MOP1-MOP5

综上所述，MOEA/D_PE算法在优化多目标测试问题时，表现出了比MOEA/D_DE、NSGA-III和MOEA/D_FRRMAB算法更好的优化性能，具有较好的收敛性能和多样性.

5 结论和未来工作

变异算子的选择是分解类多目标进化算法的重要研究方向，因为变异算子的恰当选择可以提高算法的收敛性能和多样性.本文针对变异算子选择策略问题，提出了采用个体进化状态判定策略的分解类多目标进化算法，该算法能够判定个体当前进化状态，并为个体选择恰当的变异算子，从而提高了算法的收敛精度和稳定性.通过基准测试函数的仿真实验，结果表明本文提出的算法具有良好的收敛性能和多样性.未来将继续研究采用个体进化状态判定策略的分解类多目标进化算法的实际应用问题.