简化七阶CQKF及其在SINS大失准角初始对准中的应用

2018-09-07缪玲娟邵海俊

宇航学报 2018年8期

孟东，缪玲娟，邵海俊，沈军

(北京理工大学自动化学院，北京 100081)

0 引言

捷联惯性导航系统(Strapdown inertial navigation system, SINS)的初始对准在受到外界干扰或晃动基座的影响时，经过粗对准后，其失准角较大；在此基础上进行的大失准角精对准，其状态方程具有严重的非线性。因此，需要引入非线性卡尔曼滤波方法滤波。目前，非线性卡尔曼滤波算法主要有扩展卡尔曼滤波(EKF)[1-2]、无迹卡尔曼滤波(UKF)[3-5]、容积卡尔曼滤波(CKF)[6-7]、正交容积卡尔曼滤波(CQKF)[9-10]、简化容积卡尔曼滤波(SSRCKF)[10-13]和粒子滤波(PF)[14]等，已被广泛应用到工业环境中。

传统非线性滤波算法一般最高精确到三阶精度，近年来，高阶滤波算法不断被提出来。五阶UKF[15]、五阶CKF[16]、五阶ECKF[17]、五阶ICKF[18]、高阶CQKF[9]、七阶SSRCKF[13]等高阶算法的提出，都提高了原三阶算法的滤波精度。高阶算法理论精度高，但其复杂度较高。

近年来，在信号处理的实际应用中，数据并行处理技术、高频芯片技术等技术发展不断提升了硬件功能，数据处理能力大幅度提升。因此，新的硬件系统会减轻或者消除高运算量所带来的问题；同时，高阶算法的实用性能也得到了加强。

为进一步提高滤波精度，本文提出了简化七阶CQKF(7th-SCQKF)滤波算法，并应用于SINS的大失准角初始对准中。首先，本文提出改进的简化七阶CKF(7th-MSSRCKF)滤波算法，重新推导了该算法的球-半径准则公式；其次，在7th-MSSRCKF基础上，引入正交半径准则，提出了7th-SCQKF算法，提高了滤波精度。SINS的大失准角初始对准仿真试验证明，新方法提升了滤波精度。

1 三阶容积卡尔曼滤波CKF

1.1 考虑如下非线性系统：

(1)

式中：xk为k时刻的状态向量，g(xk-1)和h(xk)为非线性函数，xk和zk分别是n维状态向量和m维量测向量；wk-1和vk分别为系统的过程噪声和量测噪声，互为不相关的零均值高斯白噪声，其统计特性为：

(2)

式中：Qk-1≥0为系统噪声方差矩阵,Rk-1>0为量测噪声方差阵矩阵,δ(k-1)j为Kronecker符号。

传统的CKF滤波器建立在非线性离散动态系统上，对任意阶函数，其积分可表示为[9]：

(x-μ)TM-1(x-μ))d(x)

(3)

式(3)可被分解为两类积分，分别为线积分和球面积分，则有：

exp(-r2/2)d(r)

(4)

(5)

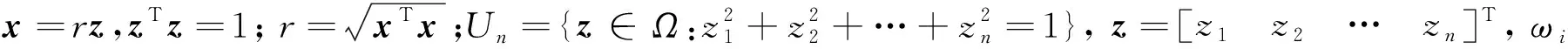
三阶CKF化简为由一组2n个等权值的容积点(采样点)来实现积分的数值逼近，共有2n个采样点。这就是CKF算法的基本思想。

2 改进的简化七阶容积卡尔曼滤波

针对多维滤波的高运算量问题，文献[10-11]提出了简化采点滤波的方法，降低了算法复杂度；文献[12]根据简化采点方法，提出了简化容积卡尔曼滤波方法(SSRCKF)，分析了估计精度为三阶和五阶的SSRCKF滤波算法；文献[13]在[12]基础上，将估计精度扩展为七阶，提出七阶SSRCKF(7th-SSRCKF)算法。本文重新推导了原7th-SSRCKF的半径线积分准则，弥补了其不足，提出改进的七阶SSRCKF(7th-MSSRCKF)算法。

2.1 改进的七阶半径线积分准则

文献[16]已经证明，如果积分公式(3)中的I(f)要达到七阶精度，就必须满足两类积分同时达到七阶精度。因此，七阶SSRCKF算法要达到七阶精度，需满足七阶半径积分准则和球面积分准则均达到七阶近似精度。改进的七阶SSRCKF算法的半径积分准则推导如下：

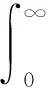
根据以上分析，对于七阶的近似精度，m=3，有4个近似方程，对于不同的k的取值，式(4)扩展为：

(6)

(7)

式(7)即为所求的七阶半径准则。

对比文献[13]，原7th-SSRCKF的七阶线积分准则，m=2，只能达到五阶的近似精度，不能达到七阶的滤波精度，而式(7)所得的七阶半径准则可以精确到七阶。因此，式(7)积分准则的推导，弥补了文献[13]的不足，提升了滤波精度。

2.2 简化七阶球面积分准则

根据文献[11,13]中的七阶球面简化准则，球面积分有(n+1)(n2+8n+6)/3个容积点，有：

(8)

(9)

其中，点集yk,uk,wk分别表示为：

(10)

(11)

(12)

将式(9)简化为：

U(f)=ωh1f(h1)+ωh2f(h2)+

ωh3f(h3)+ωh4f(h4)

(13)

则参数具体表示为：

式(13)完成了简化七阶球面积分的分解，共有采样点(n+1)(n2+8n+6)/3个。

2.3 简化七阶球-半径准则

根据式(7)和式(13)，将改进的七阶线积分准则和七阶球面简化积分准则结合起来，组成简化七阶球-半径准则。在零均值和单位方差前提下，令λ=r2/2,七阶正交简化球-半径准则可以表示为：

ωi′ωh2f(h2)+ωi′ωh3f(h3)+ωi′ωh4f(h4)

(14)

式(14)就是改进的简化七阶容积卡尔曼滤波(7th-MSSRCKF)的基本公式。根据式(4)～式(13)，式(14)中的各量均已知。由于文献[13]中七阶线积分准则的推导有缺陷，理论上就不能达到七阶的滤波精度；从理论分析可知，本文提出改进简化七阶容积卡尔曼滤波(7th-MSSRCKF)能达到七阶的滤波精度，提高了原7th-SSRCKF算法的性能。

3 七阶正交简化容积卡尔曼滤波

高阶简化CKF算法中的改进线积分准则，存在高阶扩展性难的问题。正交容积卡尔曼(CQKF)算法将线积分准则正交化，能有效地解决这个问题。

CQKF算法[8]在CKF算法的基础上，对线积分使用切比雪夫-拉盖尔多项式得到正交点，实现对线积分的采样，提高了滤波精度，并降低了容积准则的扩展难度。文献[9]中的高阶CQKF算法扩展了正交容积准则，将近似精度提高到五阶。正交准则比普通的半径准则滤波精度高[8]。

本文在高阶简化CKF基础上，引入正交容积准则，扩展了其中的半径线积分准则，提出七阶正交简化CKF(7th-SCQKF)算法，提高了滤波精度。

3.1 七阶正交简化线积分准则

对于公式(3)，根据文献[8-9]，应用高斯-拉盖尔正交准则(GGLQ)，线积分可用正交点近似为：

(15)

其中，n′为近似阶次。当维数n确定后，解方程可以得到n′个值，即n′个正交采样点，其相应的权重为：

3.2 七阶正交简化球-半径准则

根据文献[11，13]，参照第3.2节中的式(8)～式(13)，球面积分S7(r)有(n+1)(n2+8n+6)/3个容积点。式(13)是七阶正交简化CKF(7th-SCQKF)算法球面简化积分的基本形式。

根据式(13)和式(15)，将七阶正交简化线积分准则和七阶球面简化积分准则结合起来，组成七阶正交简化球-半径准则。在零均值和单位方差前提下，令λ=r2/2,七阶正交简化球-半径准则表示为：

ωi′ωh3f(h3)+ωi′ωh4f(h4)

(16)

式(16)就是七阶容积卡尔曼滤波(7th-SCQKF)的基本公式。根据式(8)～式(15)，式(16)中的各量均已知。式(16)的简化模型为：

(17)

则其相应的容积点和权值为：

εi=

(18)

ωi=

(19)

式(6)～式(19)就是7th-SCQKF的基本公式，其采样点总数为7(n+1)(n2+8n+6)/3。

4 晃动基座下SINS大失准角初始对准仿真校验

4.1 SINS的非线性初始对准模型[18-19]

由于在导航系统中存在着各种误差，所以SINS解算出的导航坐标系n′与理想的导航坐标系n并不完全重合。假设从n系到n′系可通过依次绕东西轴、天向轴、北向轴进行旋转得到，旋转角度分别为φE,φU,φN，其矢量形式定义为φ=[φEφUφN]T。此3次旋转所对应的姿态变换矩阵可分别定义为Cφ,N，Cφ,E，Cφ,U；于是得到n系到n′系的姿态变换矩阵：

(20)

(21)

4.2 仿真校验

为了进行对比，在相同SINS仿真条件下，分别利用以下3种滤波算法对整个初始对准过程进行滤波估计，3种方法分别是：UKF算法、改进简化七阶CQKF(7th-MSSRCKF)算法、七阶正交简化CKF(7th-SCQKF)算法。

在整个仿真过程中，为了检验本文所提出的滤波算法对于外界干扰的滤波能力，进行晃动基座下的初始对准仿真。假设SINS系统受到晃动基座的影响，航向角，俯仰角，横滚角作周期变化，摇摆频率分别为1 Hz，1.5 Hz，2 Hz，摇摆幅值分别为1°，3°，1°，其表达式为：

(22)

由图1～图3可知，航向角误差变化较大，俯仰角和横滚角误差变化平稳， 3种滤波算法航向角误差均在大约500 s后进入稳态， 7th-SCQKF的收敛速度比7th-MSSRCKF更快；取最后100 s航向角误差的算术平均值作为稳态误差，经过100次的Monte-Carlo仿真，3种算法姿态角稳态误差的统计结果如表1所示。