场协同原理在高超声速化学非平衡流动中的推广

刘景源

(南昌航空大学飞行器工程学院，南昌 330063)

0 引 言

发展具有高超声速巡航能力、可重复使用的新型天地往返运输系统及在大气层内的高超声速飞行器已经成为航天航空强国技术储备中需要研究的关键课题[1-2]。真实气体效应及壁面热流是高超声速飞行器空气动力学的关键问题[3]。真实气体效应和表面催化效应的共同作用对高超声速飞行器的气动加热将产生十分显著、复杂的影响。作为吸热反应的离解反应将显著地降低激波层内气体的温度；但表面催化效应所导致的复合反应放出的热量使飞行器表面热流急剧增加[3-4]。此外，真实气体的辐射效应对高超声速飞行器壁面的热流也有一定的影响[5]。

随着来流马赫数的提高，高超声速来流的总焓逐渐增大，并且来流的动能在总焓中的比重逐渐变大。经高超声速飞行器绕流的激波后，虽然总焓不变，但气体的速度降低，动能转化为静焓，导致飞行器头部附近的波后温度大幅度升高。在飞行器的中后部，虽然激波强度有所降低，波后温度有所减小，但是高速流动的流体与壁面的剪切功导致边界层内的温度急剧升高。波后及边界层内的温度升高激发了空气分子的转动、振动及电子能等能量模式(根据波后的温度不同，所激发的能量模式可能为一种或几种)，并可导致空气的离解及电离，离解过程和振动之间存在耦合，并且壁面可能为完全、有限和非催化壁面[3]。同时由于空气的离解及电离，导致了气体组分的改变。因此上述的能量转化、各能量模式的激发、离解及电离的吸热过程、振动能量的热化学非平衡过程，以及组分不均匀分布导致的扩散过程、壁面催化特性，均对高超声速飞行器的对流传热产生影响[3-4]。上述的能量过程显著区别于不可压缩及可压缩流动(无化学反应)的对流传热。

对不可压缩流动，文献[6-7]在分析速度场与温度梯度场后，指出对流传热取决于当地速度场与温度梯度场的协同，两个矢量场协同程度越高，则对流传热越好。文献[8-10]给出的大量的实验及数值模拟证明了此原理的正确性。该原理一方面统一了强化对流传热的不同观点，另一方面指出了增强或减弱对流传热的方向。随后，研究人员进行了椭圆型流动[11]、减阻流动[12]、层流与湍流的多场协同[13-14]、热质传递过程[15]等的推广工作，并进行了改进研究[16]。文献[17]将对流传热的场协同原理推广至可压缩流动中。

本文对场协同原理在高超声速化学非平衡流动的情形进行了推广，并进行了数值校验及应用研究。

1 高超声速化学非平衡流动传热场协同原理

1.1 笛卡尔坐标系下的层流流动

高超声速化学非平衡层流流动的边界层形式的能量方程如下[3]

(1)

其中H=h+u2/2、h、hs、Ds、cs分别为化学反应混合气体的总焓、静焓、组分s的焓、组分扩散系数、组分质量分数。

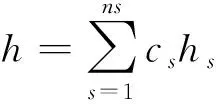
(2)

式(2)可进一步写成如下形式

(3)

对式(3)进行无量纲化

(4)

其中，L∞,ρ∞,u∞,Haw分别为高超声速化学非平衡流场的特征长度尺度、无穷远来流密度及速度、绝热恢复壁总焓；Hw为壁面焓值。St为传热壁面的Stanton数。

1.2 笛卡尔坐标系下二维湍流反应流动

对湍流流动，对文献[3]的二维高超声速化学非平衡流动的定常Navier-Stokes方程组及组分方程组引入密度加权平均[18]

(5)

并略去黏性系数与速度梯度的脉动相关(此为密度加权平均的湍流模化的惯用做法[18])，并由边界层近似[3, 19]

(6)

则二维高超声速化学非平衡流动的定常Navier-Stokes方程组及组分方程组，可简化为如下的边界层形式

(7)

(8)

(9)

(10)

(11)

(12)

对高超声速化学非平衡湍流能量方程积分也可得到高超声速化学非平衡可压缩层流式(4)类似形式，即

(13)

从上述推导可以看出，与高超声速化学非平衡层流流动的分析类似，把层流的物理量用相应的湍流平均物理量替代，即可得到高超声速化学非平衡湍流流动的场协同形式。

1.3 笛卡尔坐标系下三维高超声速化学非平衡流动

由上述推导可知，对三维高超声速化学反应流动，易分别得到与二维情况下的层流及湍流流动的对流传热式(4)与式(13)形式上类似的结果。限于篇幅，此处不再赘述。

2 数值方法及程序验证

高超声速化学反应流动采用5组分、17个化学反应的单温度模型。采用有限差分方法对高超声速化学反应模型方程组进行求解。计算所采用的数值方法详见文献[20]。本文采用文献[21]的改进的数值格式的熵修正函数进行高超声速化学非平衡流动的计算。

为验证本文所采用的数值方法及程序的准确性，采用文献[22]给出的圆柱高超声速绕流实验进行验证。图1给出了采用本文的数值计算与实验结果的对比。从图中可以看出，在实验精度范围内，本文的数值结果给出的壁面热流密度和实验测量值吻合良好，说明本文采用的数值格式及程序的正确性。

3 数值校验

以二维圆柱的高超声速化学非平衡绕流流动为例，应用节2的数值方法并结合理论分析，阐述本文给出的场协同原理的正确性。

二维圆柱绕流的来流马赫数Ma∞=20，来流温度与壁面温度之比为0.25(此温度比下的传热为冷壁对流传热问题)，雷诺数为Re=1.2×105(取长度尺度为1米)。计算采用5组分、17个化学反应的单温度模型，忽略辐射传热对热流密度的影响，并假设完全催化壁面边界条件。由于绕圆柱流动的雷诺数小，因此本计算假设绕流为层流流动。

图2给出了圆柱上的热流密度。图2的横轴坐标为圆柱圆周角度θ，而纵轴为热流密度数值(采用圆柱前驻点热流密度值归一化)。从图2可得，热流密度最大值在圆柱前驻点，从前驻点向后化学反应组分气体向圆柱壁面传热逐渐变小。

图3给出了绕圆柱流场的当地ρU及▽H矢量线分布。为清晰起见，图3在壁面法向方向每隔2个网格点给出了当地ρU及▽H矢量分布图。从图3(b)可看出，由圆柱绕流脱体激波波前总焓不变(易根据高超声速绕流的基本知识得到)，则▽H=0；而波后由于静温升高、壁面附近存在较大的温度梯度，导致▽H近似沿着圆柱径向方向。图2的圆柱壁面的热流密度分布曲线，可根据本文推广了的高超声速化学非平衡流动下的场协同原理，结合图3予以阐述。从图3可知，在圆柱前驻点，ρU和▽H平行，则夹角为180°(二矢量方向相反)，则在圆柱的前驻点热流密度最大，离开前驻点夹角迅速下降，则热流密度减小。

图4给出了圆柱绕流当地ρU及▽H二矢量协同角分布曲线，其中纵轴为场协同角β。由于该算例为高超声速化学反应流场向圆柱壁面传热，因此β大于90°。由于离开前驻点(除前驻点外)的多组分化学非平衡流动方向须沿壁面切线的方向(壁面附着流动)，则β减小较快。

4 应 用

二维双椭圆(再入大气层飞行器等高超声速飞行器常采用简单组合体外形双椭球的对称面壁面形状)来流马赫数M∞=18.8，来流温度与壁面温度之比为1.8(此温度比下的传热仍为冷壁对流传热问题)，绕流每米雷诺数为Re/m=8×106。

双椭圆外形如图5所示。该双椭圆外形是由以下两个椭圆相贯而成。

在给定的上述来流及绕流双椭圆外形条件下，根据高超声速化学非平衡绕流的基本理论，在双椭圆绕流的前驻点的边界层内▽H与壁面法向方向平行，▽H指向边界层流场方向，而当地ρU则与▽H指向相反，因此两者夹角为180°。因此，在此处对流传热热流密度最大。向流动的下游，由于高超声速绕流的附着特性，则在边界层内流动方向近似与双椭圆的壁面切向方向一致，因此当地ρU与▽H的夹角从前驻点向流动的下游迅速下降。而在上面椭圆壁面区域，根据边界层理论，层内的当地▽H近似与壁面垂直，而波后流动突遇椭圆壁面的局部凸起，当地ρU不能立即恢复到与双椭球壁面切线方向平行，当地ρU与壁面法线的夹角大于90°，从而当地ρU与▽H夹角变大，则此区域的壁面热流密度出现局部峰值。对下壁面，与节3的圆柱绕流类似，流动流过前驻点后，热流密度迅速单调下降。

为验证上述应用推广了的场协同原理理论解释双椭圆壁面热流密度结论的正确性，采用节3的数值方法进行数值验证。

图6与图7分别给出了双椭圆上壁面的热流密度分布曲线(用驻点处的热流密度进行了归一化处理)及边界层内当地ρU与▽H协同角度。图6双椭圆的驻点处的热流密度最大值及上壁面局部凸起区域热流密度的局部极大值可用图7的两矢量协同角分布曲线解释，即局部热流密度的峰值对应局部的协同角度的极大值。因此基于本文给出的高超声速化学非平衡下的场协同原理的理论阐述与数值模拟结果相符。

5 讨论及分析

本节以二维高超声速化学非平衡流动的边界层近似下的场协同理论为例，对上述的场协同原理进行了讨论及分析。但应该指出的是本节的讨论对三维边界层亦成立。

5.1 高超声速化学非平衡层流流动的场协同原理

把总焓表达式代入式(2)中，

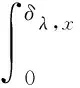
(14)

从式(14)可以看出，对高超声速化学非平衡流动的对流传热场协同原理，传热的贡献包括单位体积的动量与静焓的协同、动量和当地主流方向速度梯度的协同。

进一步，由笛卡尔坐标系的可压缩边界层型的动量方程，可把式(14)右端第二项改写为

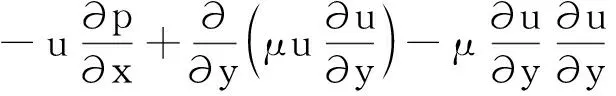
(15)

把式(15)代入式(14)，考虑到式(15)右端第二项积分近似为零，则

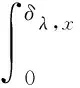
(16)

从式(16)可知，对高超声速化学非平衡反应流动的壁面热流密度，不但包括单位体积的动量与静焓梯度的协同，还计及了压力梯度、可压缩耗散函数等的影响。考虑到静焓的定义，则协同计及了所有组分的平动能、转动能、振动能及电子能及零点能梯度的贡献。另外，从式(16)也可以看出，当流动存在逆压梯度时，压力梯度对热流具有减弱作用，反之则具有增强作用；由于耗散函数始终大于零，因此其对热流场的影响始终具有减弱效果。

5.2 高超声速化学非平衡湍流流动的场协同原理

类似对高超声速化学非平衡层流流动的分析，对湍流的场协同原理的分析，除可得到层流流动的场协同原理的特点处，还包括了湍流剪切应力的贡献，此处从略。

5.3 高超声速热化学非平衡层流及湍流流动的场协同原理

本节以三温度模型[23]为例，论述场协同原理形式上与采用的温度模型无关。

根据文献[3, 23]，由三温度模型下的高超声速热化学非平衡流动的能量边界层方程，类似1节的方法，可推得三温模型下的高超声速热化学非平衡流动的场协同

(17)

其中Tv、Te分别为振动温度及电子温度；λv、λe分别为振动温度及电子温度下的热传导系数。

式(17)亦可写成类似式(4)及式(13)的无量纲形式，此处从略。

由式(17)具体形式可知，对三温模型，热流密度亦为当地单位体积的动量与单位质量总焓梯度的协同，场协同原理形式上与采用的温度模型无关。

应该指出虽然以三温模型为例进行了论述，对双温[24]及多温模型[25]，本节给出的结论亦成立。另外，节5.1及5.2的讨论对双温[24]、三温[23]及多温模型[25]亦成立。再者，虽然本小节仅对层流流动进行了分析，但是上述结论对湍流流动也是成立的。

5.4 高超声速层流及湍流流动的场协同原理的对比及分析

从节1.1与节1.2的结果可以看出，层流流动的式(3)、(4)分别与湍流流动的式(12)、(13)形式上一致。

虽然层流与湍流的场协同原理表达形式上一致，但是在物理上和数学上确有不同。从物理上，湍流的脉动量大，扩散效应显著大于相应的层流流动，因此一般来说可增大对流传热。从控制方程上，从组分方程(8)可见，湍流影响化学反应速率；从动量方程(9)也可以看出，湍流的雷诺剪切应力也影响对流场的平均速度型；从能量方程(11)，湍流的雷诺剪切应力及湍流热通量等项均影响平均的密度、速度及总焓的数值。并且必须满足连续方程(7)的限制性条件。

因此，上述的湍流效应均对流场的平均物理量产生影响，进而导致了流场的平均密度、平均速度、平均温度，平均的总焓及其梯度有别于相应的层流流动。

另外，由于平均总焓包括了湍动能项，并且对高超声速流动，流场总焓中的湍动能一般不能忽略[18]，这也是层流流动与湍流的区别。

6 结 论

在高超声速飞行下，绕飞行器的空气受强激波以及飞行器磨擦等因素的加热而发生离解和电离。此时空气不能再被视为完全气体，而是由分子、原子、离子和电子组成的真实气体。这些原子和离子的扩散及复合(包括在飞行器表面上的壁面催化效应)将伴随着大量的能量交换。因此绕复杂外形飞行器的高超声速流场是由空气动力学及化学热动力学中产生的、带有化学反应的复杂流动，所涉及的流动现象包括从微观到宏观的高温物理化学变化。上述情形都是有别于无化学反应的可压缩流动的。本文则将对流传热的场协同原理从不可压缩流动推广至高超声速化学非平衡流动中，并得到以下结论。

(1) 高超声速化学非平衡及高速化学反应等流动的传热量(热流密度)取决与当地单位体积的动量(当地密度与速度矢量的乘积)与单位质量总焓梯度的协同程度。该协同对高超声速化学、热化学非平衡及高速化学反应的层流和湍流流动的对流传热问题均适用。

(2) 用当地单位体积的动量与单位质量总焓梯度的协同研究高超声速化学非平衡及高速化学反应的壁面热流密度问题，对层流流动的对流传热问题，不但计及了流动的当地密度变化对壁面热流密度的作用，而且包含了当地静焓梯度、压强梯度及边界层内的分子黏性剪切效应对壁面热流密度的影响；对湍流流动的壁面热流密度，除了上述各项(密度加权平均下的各项)对热流密度的影响外，还计及了密度加权平均下的雷诺剪切应力对壁面热流密度的作用。考虑到高超声速化学非平衡流静焓的定义，则协同同时计及了所有组分的平动能、转动能、振动能及电子能的梯度的贡献。