四方相多铁BiMnO3电控磁性的理论研究∗

袁野 田博博 段纯刚

(华东师范大学信息科学技术学院,极化材料与器件教育部重点实验室,上海 200241)(2018年5月12日收到;2018年6月15日收到修改稿)

1 引 言

近年来,人工智能由于其未来在各行各业中的巨大应用潜力而受到了广泛关注.其中,人工神经网络[1,2]是一个通过硬件来实现人工智能的有力方法.这是依靠人工突触器件在硬件方面模拟人类大脑工作方式[3−5]的新型的实现人工智能的方向.它在硬件结构上颠覆了传统的冯诺依曼式架构的计算机结构,只依靠人工突触器件来模拟人脑中神经元细胞之间的电学信号传输,从而在此基础上实现类脑芯片[6]的产生.相比于过去基于冯·诺依曼式架构的软件算法类型的人工智能,这类结构类型的类脑芯片的优势在于它是高度并行的,并且具有更轻便的体量、更快的运算速度以及更低的能量消耗[7].

对于构建仿脑芯片来说,最关键的是在于构造类比神经元和突触的计算和塑性功能的电子器件[8−12].作为人工突触器件,需要具有能够通过外加电场来控制其阻值连续变化的特性,从而实现突触权值的连续更新[13].而铁电材料的铁电极化是受外场高度可控的,所以只要满足铁电极化调控电阻变化的器件都可以用来构造铁电型人工突触器件[14−16].而多铁材料在具备铁电性的同时,还具备铁磁性,这种优势在人工突触领域具有更大的潜力,而目前多铁人工突触器件方面的研究几乎是一片空白,有待进一步的探索.

BiMnO3作为一种多铁材料[17−19],其内部同时存在着铁电性与铁磁性等多种铁序并存,并且其不同铁性之间存在着相互耦合作用.这就使得多铁体BiMnO3在作为人工突触器件材料时,相比于纯粹的铁电材料,其铁电与铁磁之间的耦合作用使得它具有更多可调控的自由度,从而能够实现性能调控的突触器件.铁磁性本身也可以通过搭建磁隧道结来实现自旋神经元器件[20−22].这些都使得多铁材料在人工突触器件方面具有潜在的应用价值.

本文通过第一性原理计算的方法,对施加两种不同应力的四方相BiMnO3的铁电特性及其磁矩随铁电性的变化进行了计算研究,展示出了BiMnO3在构建多铁人工突触器件方面的应用潜力,对于未来构造多铁型人工神经元器件提供了一定程度的理论指导,对于类脑芯片的发展也具有一定的意义.

2 模型构建与计算方法

2.1 模型构建

计算所用的理想模型是BiMnO3的四方相钙钛矿结构.该结构是在立方相钙钛矿结构的基础上,施加xy面内应力,导致其在z方向上拉伸,形成的四方相结构.本文分别采用两种四方相结构,如图1所示,一种是xy面内施加0.18%应力的四方相结构,另一种是xy面内施加4%应力的四方相结构.立方相BiMnO3的晶格常数在Perdew-Burke-Ernzerhof(PBE)[23]方法下的最优值为a=3.894 Å.0.18%应力下的a=3.887 Å,c=3.908 Å;4%应力下的a=3.738 Å,c=4.071 Å.

图1 钙钛矿型BiMnO3的晶体结构 (a)立方相BiMnO3;(b)0.18%应力下的四方相BiMnO3;(c)4%应力下的四方相BiMnO3Fig.1.Crystal structure of perovskite BiMnO3:(a)Cubic;(b)tetragonal BiMnO3with 0.18%strain;(c)tetragonal BiMnO3with 4%strain.

在铁电或多铁材料中,自发极化会带来束缚电荷从而产生退极化场,使得静电能升高,导致均匀极化的状态是不稳定的,所以铁电或多铁材料中往往存在很多铁电畴,这使得外加电场所导致的铁电翻转往往是一部分铁电畴中极化方向的翻转,对于材料整体来说,其铁电翻转是不完全的.本文中单个BiMnO3原胞的不同极化强度是对这种不完全的铁电翻转进行的近似处理.

2.2 计算方法

本文中的计算是采用密度泛函理论体系下的投影缀加平面波(PAW)方法[24−26].其中,交换关联赝势采用的是广义梯度近似(GGA)中的PBE近似[23].对于PAW的平面波展开,使用500 eV的截断能.第一布里渊区按10×10×10划分网格选取k点.对布里渊区的积分计算采用的是施加布洛赫修正的四面体方法[27].自洽收敛精度为1×10−6eV/atom.因为GGA在计算中往往低估总交换能,所以计算通过引入Hubbard参数U(库仑作用能)来修正电子间的轨道相关作用[28],所有体系中Mn的3d电子态取值U=4 eV.

3 结果与讨论

施加两种应力下的四方相BiMnO3的铁电双势阱曲线[29]以及Mn原子磁矩随铁电极化强度的变化曲线如图2所示.图中横坐标为以Mn原子与O原子在[001]方向上的相对位移来确定的软模形变幅度,其中,0对应顺电相,1.0对应极化方向为沿[001]方向向上的铁电相,−1.0对应极化方向为沿[001]方向向下的铁电相.如果一个体系的总能量随着该软模形变幅度表现出双势阱曲线,则说明该体系具有铁电相.从图2可以看出,在两种应力下的四方相BiMnO3均具有明显的铁电极化;而Mn原子的磁矩随着极化强度的改变也有一定程度的变化;当四方相BiMnO3由顺电相过渡为铁电相的过程中,Mn原子的磁矩逐渐增大.

通过图2(a)可以看出,在xy面内施加0.18%应力下的四方相BiMnO3的Mn原子磁矩在铁电相与顺电相中的差别为0.06µB左右,相对较小.而通过图2(b)可以看出,在xy面内施加更多应力的条件下即4%应力下,四方相BiMnO3的Mn原子磁矩在铁电相与顺电相中的差别在一定程度上有所增加,即0.15µB左右.这种幅度的磁矩变化虽然有限,但至少可以定性地表明四方相BiMnO3的Mn原子磁矩的大小可以由外加电场通过其材料的铁电极化强度来进行一定程度的调控,并且在xy面内施加越大的应力,不同极化强度下对应的磁矩变化也就越大.

图2 四方相BiMnO3的铁电双势阱曲线及Mn原子磁矩随铁电极化强度的变化 (a)0.18%应力;(b)4%应力Fig.2.Ferroelectricity double-well potential curves of tetragonal BiMnO3and magnetic moment of Mn:(a)0.18%strain;(b)4%strain.

四方相BiMnO3单胞中Mn原子的磁矩随其铁电极化强度变化的原因,在于其中Mn原子与O原子之间的轨道杂化的改变.如图3所示,态密度的正值与负值分别代表多数自旋态与少数自旋态.在能量为−4—−1 eV的范围内时,Mn的3d轨道主要由多数自旋态占据.在4%应力条件下,当四方相BiMnO3由顺电态过渡为极化方向沿[001]方向向上的铁电态时,Mn原子与[001]方向顶部的O原子之间的键长就会减小.这导致Mn原子与O原子之间的轨道交叠部分增加,从而使得费米能级以下且靠近费米能级处的Mn原子的3d电子态向着深能级方向发生移动,这意味着Mn的3d电子占据数的增加,从而导致了Mn原子的磁矩的增大.其中,Mn的3d电子占据数的增加部分来源于O的2p电子轨道占据的减少.在这里,单胞极化强度的改变,近似代表了实验中部分铁电畴的翻转,而不同的铁电极化强度,则近似代表了实验中铁电畴的翻转比例.这意味着在实验上依靠外加电场实现不同比例的铁电畴的翻转,就可以实现对四方相BiMnO3中Mn原子整体表现出的宏观磁矩的调控.

为了更好地理解四方相铁电性与铁磁性之间的关系,我们绘制了施加4%应力下的四方相BiMnO3的顺电态与铁电态在xz面的自旋密度分布图,如图4所示.从图4可以看出,四方相BiMnO3的Mn原子与O原子相对位移产生的铁电极化改变了Mn与O之间的轨道杂化,从而在一定程度上增强了Mn原子的磁矩,导致在自旋密度分布图中的顺电相与铁电相分别呈现出两个不同的铁磁态,即一个相对较弱的铁磁态和一个相对较强的铁磁态.

图3 在4%应力下的四方相BiMnO3分波态密度图 (a)Mn原子3d轨道;(b)[001]方向顶部O原子2p轨道;其中灰色部分为顺电态,红色实线为铁电态Fig.3.Orbital-resolved density of states(DOS)for tetragonal BiMnO3with 4%strain:(a)Mn 3d;(b)Otop2p.The shaded plots and solid red curves correspond to the DOS of atoms at paraelectric states and ferroelectric states,respectively.

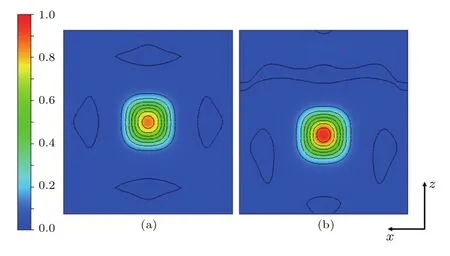
图4 施加4%应力下的四方相BiMnO3的顺电态与铁电态在xz面的自旋密度 (a)顺电态;(b)铁电态Fig.4.Spin density distribution in the xz plane for the tetragonal BiMnO3with 4%strain:(a)Paraelectric states;(b)ferroelectric states.

多铁BiMnO3中的铁电性对铁磁性的调控作用在人工突触器件中具有潜在的应用价值.通过这两种铁性之间的耦合,在构造人工突触器件时,可以用来模拟生物突触的多种复杂行为.以图5为例,真实生物的突触在工作时,存在着某些突触在传递信号的过程中影响着其他突触传递信号的行为,换句话说,就是一些突触的信号传递过程可以调控另一些突触的信号传递过程,而这种复杂的行为可以利用以BiMnO3为代表的多铁体材料搭建人工突触器件来实现.如图5所示,多铁材料存在铁电性,可以通过水平方向的外加电场调节铁电极化状态进而通过影响界面势垒改变其电阻态,而如果将两个多铁材料在垂直方向上搭建多铁隧道结的话,那么由于每个多铁材料的磁矩都可以由其铁电极化强度来调控,而磁矩的变化就可以根据磁隧道结的原理实现在垂直方向上的阻态调控.这种结构在实现水平方向上阻态调控的同时可以由水平方向的电输运性质进一步调节垂直方向的阻态,就可以实现生物突触的一些复杂行为的模拟.

图5 模拟复杂突触行为的多铁人工突触器件示意图(a)生物突触传递信号的同时影响其他突触传递信号的行为;(b)多铁型人工突触器件结构;蓝色为电极,黄色为绝缘隧穿层Fig.5.(a)Complex behavior of synapse;(b)schematic illustration of multiferroic synapse;the blue and yellow particles correspond to the electrodes and insulator,respectively.

4 结 论

通过基于密度泛函理论的投影缀加平面波方法,采用GGA+U计算了四方相BiMnO3在xy面内施加0.18%与4%两种不同应力条件下的铁电与铁磁性质,并且探究了二者之间的耦合作用.结果表明,在多铁体BiMnO3中,其铁磁性可以通过其铁电性进行一定程度的调控,使其在作为人工突触器件材料中具有更多可调控的自由度,从而可以用于模拟多突触连接,为将来构造类脑芯片打下一定的基础.本文所揭示出的多铁材料在人工神经网络中的潜力,也对人工智能领域的发展具有一定的意义.