高中数学运算能力培养路径探索
2018-09-04林传利
林传利
(连江第一中学,福建 福州350500)
一、识记定理公式,夯实运算基础
与初中数学相比,高中数学概念多抽象性强,公式和定理多,且运算量与思维量大,面对公式如何能更好的识记并应用,如何更好要熟练掌握公式的变形和逆用。在新课讲授时,尽可能创设情景产生知识冲突,急需引入新的公式和定理,方可解决所遇问题。通过具体典例不断巩固,加强辨析,强化记忆,才能熟能生巧,信手拈来。教学时师生对知识产生过程进行共同推导和总结,通过类比,抓住特征,从而不断夯实基础,真正做到根深叶茂。
在利用导数知识来研究切线、函数单调性、极值、最值等问题时,学生对解决问题的基本思路是清晰的,先考虑函数定义域再求函数的导函数,由导函数的正负值来判断函数的单调性,进而求函数的极值、最值。但在解题过程中最关键地是正确求出导函数,而求导函数有八个公式四个运算法则,往往还要涉及复合函数的求导问题,这都会给学生造成一定的障碍。
教师要注重每次考试或练习中学生出现问题的讲评,师生共同分析是什么原因造成的,学生的失分点就是教学的关注点、重点。有些问题虽已强调多次,学生上课似乎也听懂了,但在考试中还是暴露出基础不扎实,对题中易错点不能很好掌握。例如已知函数f(x)=2ax-ln(2x),x∈(0,e],a∈R,当a=1时,求f(x)的单调区间和极值。此题是常规问题难度不大,学生能很好形成解题思路,但有一部分学生不能正确求出导函数,主要是没有把1n(2x)看成复合函数而当作初等函数求导,从而得到导致一步算错步步错,非常地可惜。所以教学中不能仅仅停留在“同学们,要好好算”这样正确的废话上,而是精心挑选典型例题,尽可能为学生设置一些易错点,让学生自已去闯、去体验,然后总结经验与教训,吃一堑长一智,争取不犯类似错误。
二、选择合理算法,优化运算过程
在解答选择、填空题时要根据题目所给条件选择不同的方法,尽量多思少算,提高解题速度,节约一定的解题时间。教学中要训练学生可以从多角度、多方位去寻找解决问题的方法,可选用排除法、特例法、验证法、估算法、数形结合法等方法。[1]解答时认真审题,充分挖掘题目中隐含条件,利用已知条件与性质,减少不必要的运算。拓宽解题思路,通过比对,不断提炼,引导学生总结解题规律,形成技能。在平常教学或课外练习,要精心选择典型例子,巧用一题多解渗透数学运算核心素养。
在解决数学问题中,常遇到学生运算方向不合理,运算对象不清晰。如何提高运算的合理性,是教学中应关注的一个难点,如果运算方向正确,选择合适方法可提高解题的正确率,还大大提高解题效率。下面是一道单元测试的填空题讲解的课堂实录。
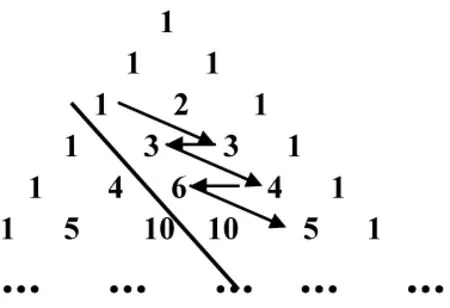
如图,在杨辉三角形中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数形{an}。1,3,3,4,6,5,10,…记其前n项和为Sn。则S21的值是____?
学生1:拿到题目,通过观察发现,该数列可分成求奇数项和与偶数项和,然后再将两个结果加起来。奇数项构成的新数列为1,3,6,10…66,偶数项构成数列是3,4,5,6,…12,而奇数项后一项减前一项是一个等差数列,偶数项是以3为首项,以1为公差的等差数列。从而可以将奇数项所有项写出来并求得286,而偶数项的和为75,所以S21=361。
师:如果本题改为求前41项之和?那奇数项又是多少?
学生2:设奇数项构成新数列记为{bn},则b2-b1=2,b3-b2=3,b4-b3=4,…,bn-bn-1=n由累加法得数列{bn}的通项再利用分组求和办法可得286,偶数项和为75。若求前41项之和思路一样。
师:这给大家提供一种求此类问题的一般性方法,很棒!
学生3:上面方法运算过程相对有点复杂,若将所有项一一写出来有难度,方法二用分组求和后的求解过程也不易。本题可以利用二项式系数性质来求解……
在解题教学中,引导学生解后反思,不能满足于解出答案,要搞清命题意图,想考查什么,是否还有更简捷的方法,蕴含什么算理、算法。讲解时不能只感动教师自已,让学生感到教师方法的妙,而要从不同角度进行分析,抓住问题本质,拓宽解题视野,不断优化运算过程。
三、重视变式训练,提升运算思维
教学中要重视教材中例题与习题,这些题目是编写者为配合基本知识精心挑选的,具有很强的代表性和导向性。教学时要注重对题目进行挖掘,最简单地就把条件与结论进行对调,或者改变条件范围。当然如何进行改编、嫁接、加工,需要教师平时勤阅读,多积累,随时记录,善于总结并实现知识迁移。在学习“杨辉三角”与二项式系数的性质时,教材先用赋值法令x=1从而得出展开式中奇数项的二项式系数的和等于偶数项的二项式系数的和。为进一步加深理解二项式系数之和与项的系数之和等相关知识,通过下列变式进行训练。
本题关键是弄清所求是哪些项的系数,利用赋值法来求解相对较为容易。第一问是求常数项系数,与x无关令x=0得到a0=2100;第二问求得是所有项的系数的和,令x=1就可得到;第三问通过观察,可由奇次项的系数和为同理可求偶次项的系数和为所赋的值应根据所求展开式的系数和的特征来确定,有了前面的铺垫教学,学生还是能较好地掌握好。
本题要求系数最大的项关键是先要求出n的值,然后利二项展开式的通项公式来求。实际上是如何求出由通项公式可知所有奇数项的系数为正,所有偶数项的系数为负,加了绝对值之后就是展开式的所有系数之和2n,故由2n=128得n=7。题目再改为展开式中偶数项二项式系数的和比(a+b)n展开式的各项系数和大112?利用偶数项二项式系数的和是所有二项式系数和的一半,可列式22n-1=2n+112从而解出n=4,其他问题就迎刃而解了。
变式3:已知(1-2x)7=a0+a1x+a2x2+ …+a7x7,求代数式+2a1a3+…+7a1a7的值。
学生看到题目会想到提取a1得到a1(a1+2a2+3a3+…+7a7),但又不能直接利用赋值法来求a1,有学生提出利用通项公式先求出a1,分别求出a2,a3,…,a7,想到计算量太大就放弃了。进一步引导学生观察所求式子结构特征,引导学生思考这个式子怎样才能得到,联想到幂函数求导公式,将等式两边分别求导可得7×(-2)×(-2x)6+a1+2a2x+3a3x2+… +7a7x6,令x=0得a1=-14,令x=1得a1+2a+3a3+…+7a7=-14从而求得代数式为196。
通过上面几个变式训练,让学生进一步认识到求二项展开式系数的问题时,本质上都采用赋值法和二项式系数和公式来解决相关问题。教学中要充分考虑学生思维渐变过程,不宜操之过急应适时减慢教学速率。变式训练由易到难,先简单的模仿,不断加强题目限制条件,引导学生思考进行思想碰撞,真正内化所学内容。
数学运算是学好数学的基础,是分析、解决数学问题一项基本技能。[2]在日常教学中教师要有意识多引导,通过多种形式进行训练,让学生多思、多想、多算,加大动手演算能力,逐步培养学生恒心、耐心和毅力等品质。而数学运算能力的提升是一个循序渐进的过程,需要长期训练,日积月累,做教与学的有心人。
